
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Целочисленные ЗЛП, графический метод решения в случае двух переменных.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
При наличии в задаче линейного программирования двух переменных, а в системе ограничений неравенств задача может быть решена графическим методом. В системе координат X 10 X 2 находят область допустимых решений, строят вектор C и линию уровня. Перемещая линию уровня по направлению C для задач на максимум, определяют наиболее удаленную от начала координат точку и ее координаты. В случае, когда координаты этой точки нецелочисленные, в области допустимых решений строят целочисленную решетку и находят на ней такие целые числа Аналогично решается задача на минимум. Целочисленному минимуму целевой функции будет соответствовать координата вершины целочисленной решетки, лежащей в области допустимых решений, наиболее близкой к началу координат в направлении вектора C. Рассмотрим алгоритм решения задачи целочисленного программирования на конкретном примере. Пример: Для улучшения финансового положения фирма приняла решение об увеличении выпуска конкурентоспособной продукции, для чего в одном из цехов необходимо установить дополнительное оборудование, требующее Зная, что для установки одного комплекта оборудования 1-го вида требуется 2м2 площади, а для оборудования 2-го вида — 1м2 площади, определить такой набор дополнительного оборудования, который дает возможность максимально увеличить выпуск продукции. Решение: Составим математическую модель задачи. Предположим, что фирма приобретает Математическая модель задачи будет иметь вид:
при ограничениях:
Получим задачу целочисленного программирования. Так как неизвестных только два (
Рис. 41.1 OABC — область допустимых решений (ОДР). Оптимальное решение задача имеет в точке B (9/5,41/15) при этом максимальное значение целевой функции составляет 218/15 ед. Полученное оптимальное решение не целочисленное. Условию целочисленности переменных удовлетворяют координаты 12 точек, принадлежащих ОДР. Чтобы найти точку, координаты которой определяют решение исходной задачи, заменим многоугольник OABC многоугольником OKEMNF, содержащим все допустимые точки с целочисленными координатами. Строим вектор получим в точке E (1, 3) максимальное значение целевой функции
Ответ: Фирме следует приобрести один комплект оборудования 1-го вида и три комплекта оборудования 2-го вида, что обеспечит ей при имеющихся ограничениях на производственные площади и денежные средства максимальное увеличение выпуска продукции, равное 14 ед. в смену.
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.117 (0.006 с.) |

 и
и  , которые удовлетворяют системе ограничений и при которых значение целевой функции наиболее близко к экстремальному нецелочисленному решению. Координаты такой вершины и являются целочисленным решением.
, которые удовлетворяют системе ограничений и при которых значение целевой функции наиболее близко к экстремальному нецелочисленному решению. Координаты такой вершины и являются целочисленным решением.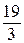 м2 площади. На приобретение дополнительного оборудования фирма выделила 10 тыс. ден. ед., при этом она может купить оборудование двух видов. Приобретение одного комплекта оборудования 1-го вида стоит 1 тыс. ден. ед., 2-го вида — 3 тыс. ден. ед. Приобретение одного комплекта оборудования 1-го вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования 2-го вида — на 4 ед.
м2 площади. На приобретение дополнительного оборудования фирма выделила 10 тыс. ден. ед., при этом она может купить оборудование двух видов. Приобретение одного комплекта оборудования 1-го вида стоит 1 тыс. ден. ед., 2-го вида — 3 тыс. ден. ед. Приобретение одного комплекта оборудования 1-го вида позволяет увеличить выпуск продукции в смену на 2 ед., а одного комплекта оборудования 2-го вида — на 4 ед.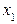 комплектов дополнительного оборудования 1-го вида и
комплектов дополнительного оборудования 1-го вида и  комплектов оборудования 2-го вида.
комплектов оборудования 2-го вида.
 ,
, ,
,  ,
, 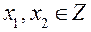 .
.
 . Линию уровня перемещаем по направлению
. Линию уровня перемещаем по направлению  ,
, (ед.)
(ед.)


