
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Виды злп и способы перехода от одного вида к другому.Содержание книги
Поиск на нашем сайте
Одна и та же ЗЛП может быть сформулирована в различных эквивалентных формах. Наиболее важными формами задачи линейного программирования являются каноническая и стандартная. В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х1, х2,..., хn являются неотрицательными:
К канонической форме можно преобразовать любую задачу линейного программирования. Правило приведения ЗЛП к каноническому виду: 1. Если в исходной задаче некоторое ограничение (например, первое) было неравенством, то оно преобразуется в равенство, введением в левую часть некоторой неотрицательной переменной, при чем в неравенства «≤» вводится дополнительная неотрицательная переменная со знаком «+»; в случаи неравенства «≥» - со знаком «-»
Вводим переменную
Тогда неравенство (32.1) запишется в виде:
В каждое из неравенств вводится своя “ уравнивающая ” переменная, после чего система ограничений становится системой уравнений. Число вводимых дополнительных неотрицательных переменных при преобразовании ограничений-неравенств в ограничения-равенства равно числу преобразуемых неравенств. Вводимые дополнительные переменные имеют вполне определенный экономический смысл. Так, если в ограничениях исходной задачи линейного программирования отражаются расход и наличие производственных ресурсов, то числовое значение дополнительной переменной в плане задачи, записанной в основной форме, равно объему неиспользуемого соответствующего ресурса. 2. Если в исходной задаче некоторая переменная не подчинена условию неотрицательности, то ее заменяют (в целевой функции и во всех ограничениях) разностью неотрицательных переменных 3. Если в ограничениях правая часть отрицательна, то следует умножить это ограничение на (-1) 4. Наконец, если исходная задача была задачей на минимум, то введением новой целевой функции F1 = -F мы преобразуем нашу задачу на минимум функции F в задачу на максимум функции F1. Таким образом, всякую задачу линейного программирования можно сформулировать в канонической форме. В стандартной форме задача линейного программирования является задачей на максимум (минимум) линейной целевой функции. Система ограничений ее состоит из одних линейных неравенств типа «<=» («>=»). Все переменные задачи неотрицательны.
Всякую задачу линейного программирования можно сформулировать в стандартной форме. Приведение к стандартной форме необходимо, таккакбольшинство методов решения задач линейного программирования разработано именно для стандартной формы. Для приведения к стандартной форме задачи линейного программирования может потребоваться выполнить следующие действия: - перейти от минимизации целевой функции к ее максимизации; - изменить знаки правых частей ограничений; - перейти от ограничений-равенств к неравенствам; - избавиться от переменных, не имеющих ограничений на знак.. Примеры: 1. Привести к каноническому виду задачу
Введем дополнительные переменные x3 , x4 , x5. Причем в первое неравенство введем неотрицательную переменную x3 со знаком минус, а во второе и в третье – со знаком плюс переменные x4 , x5 запишем задачу в виде:
что и дает эквивалентную задачу в канонической форме. 2. Привести к стандартному виду задачу
Выразим через
Целевая функция будет выглядеть следующим образом:
Или, после упрощения:
Так как Итак, эквивалентная задача в стандартной форме будет выглядеть следующим образом:
|
|||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 4409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.54.188 (0.008 с.) |

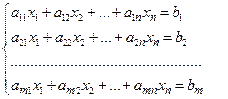


 (32.1)
(32.1)


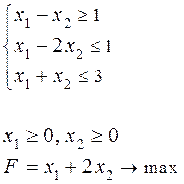





 и
и  остальные переменные:
остальные переменные: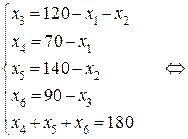

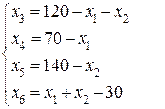


 , то перепишем нашу систему следующим образом:
, то перепишем нашу систему следующим образом: 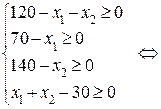
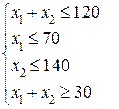 .
.



