
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм применения метода «золотого сечения».Содержание книги
Поиск на нашем сайте
1) На первой итерации заданный отрезок делится двумя симметричными относительно его центра точками и рассчитываются значения в этих точках. 2) После чего тот из концов отрезка, к которому среди двух вновь поставленных точек ближе оказалась та, значение в которой максимально (для случая поиска минимума), отбрасывают. 3) На следующей итерации в силу показанного выше свойства золотого сечения уже надо искать всего одну новую точку. 4) Процедура продолжается до тех пор, пока не будет достигнута заданная точность. Формализация 1. Шаг 1. Задаются начальные границы отрезка 2. Шаг 2. Рассчитывают начальные точки деления:
и значения в них целевой функции:
Если Иначе 3. Шаг 3. Если Иначе возврат к шагу 2. Решение задач нелинейного программирования методом Фибоначчи. В силу того, что в асимптотике Алгоритм применения метода Фибоначчи. Шаг 1. Задаются начальные границы отрезка
и значения в них целевой функции:
Шаг 2. Если Иначе Шаг 3. Если Иначе возврат к шагу 2 Задача 2. Пример решения задач нелинейного программирования методом Фибоначчи. Найти min функции f(x)=18 Решение: Fn+1 = F10 = 55; Fn+1 = F9 = 34; Fn = F8 = 21; Fn-1 = F7 = 13; Fn-2 = F6 = 8; Fn-3 = F5 = 5; Fn-4 = F4 = 3; Fn-5 = F3 = 2; Fn-6 = F2 = 1; Fn-7 = F1 = 1; Итерация 1. Х11 = а + X21 = a+ f (x11)=18x2 - 20x - 32= 18 ∙(15,2)2 – 20∙ (15,2) - 32 = 4158,72 - 304 - 32 = 3822,72 f(x21)= 18x2 - 20x – 32=18∙(24,72)2 – 20∙(24,72) - 32 = 10998 - 494,4 - 32=10471,6 f(x11) < f(x21), следовательно отрезок ограничен [ 0; 24,72 ]. Итерация 2. x12 = a + x22 = a + f(x12) = 18x2 - 20x – 32 = 18 ∙ (9,4)2 – 20 ∙ (9,4) – 32 = 1590,48 – 188 - 32 = 1370,48 f(x22)= 18x2 - 20x – 32 = 18 ∙ (15,3)2 – 20 ∙ (15,3) – 32 = 4213,62 – 306 – 32 = 3875,62
f(x12 ) < f(x22 ), следовательно отрезок ограничен [ 0; 15,3 ]. Итерация 3. x13= a + x23= a + f(x13) = 18x2 - 20x – 32 = 18 ∙ (5,8)2 – 20 ∙ (5,8) – 32 = 605,52 – 116 – 32 = 457,52 f(x23) = 18x2 - 20x – 32 = 18 ∙ (9,5)2 – 20 ∙ (9,5) – 32 = 1624,5 – 190 – 32 = 1402,5 f(x13) < f(x23), следовательно отрезок ограничен [ 0; 9,5 ]. Итерация 4. x14 = a + x24 = a + f(x14) = 18x2 - 20x – 32 = 18 ∙ (3,61)2 – 20 ∙ (3,61) – 32 = 234 – 72,2 – 32 = 129,8 f(x24) = 18x2 - 20x – 32 = 18 ∙ (5,8)2 – 20 ∙ (5,8) – 32 = 605,52 – 116 – 32 = 457,52 f(x14) < f(x24), следовательно отрезок ограничен [ 0; 5,8 ]. Итерация 5. x15 = a + x25 = a + f(x15) = 18x2 - 20x – 32 = 18 ∙ (2,18)2 – 20 ∙ (2,18) – 32 = 85,5 – 43,6 – 32 = 9,9 f(x25) = 18x2 - 20x – 32 = 18 ∙ (3,63)2 – 20 ∙ (3,63) – 32 = 237,06 – 72,6 – 32 = 132,46 f(x15) < f(x25), следовательно отрезок ограничен [ 0; 3,63 ].
Итерация 6. x16 = a + x26 = a + f(x16) = 18x2 - 20x – 32 = 18 ∙ (1,5)2 – 20 ∙ (1,5) – 32 = 40,5 – 30 – 32 = -21,5 f(x26) = 18x2 - 20x – 32 = 18 ∙ (2,2)2 – 20 ∙ (2,2) – 32 = 87,12 – 44 – 32 = 11,12 f(x16) < f(x26), следовательно отрезок ограничен [ 0; 2,2 ]. Итерация 7. x17 = a + x27 = a + f(x17) = 18x2 - 20x – 32 = 18 ∙ (0,726)2 – 20 ∙ (0,726) – 32 = 9,486 – 14,52 – 32 = -37,034 f(x27) = 18x2 - 20x – 32 = 18 ∙ (1,47)2 – 20 ∙ (1,47) – 32 = 38,88 – 29,4 – 32 = -22,52 f(x17) < f(x27), следовательно отрезок ограничен [ 0; 1,47 ]. Итерация 8. x18 = a + X28 = a + f(x18) = 18x2 - 20x – 32 = 18 ∙ (0,735)2 – 20 ∙ (0,735) – 32 = 9,72 – 14,7 – 32 = -36,98 f(x28) = 18x2 - 20x – 32 = 18 ∙ (0,735)2 – 20 ∙ (0,735) – 32 = 9,72 – 14,7 – 32 = -36,98 f(x18) = f(x28) = -36,98 – точка min функции. Ответ: min f(x)= -36,98 Заключение Математическое моделирование как инструмент познания завоевывает все новые и новые позиции в различных областях деятельности человека. Оно становится главенствующим направлением в проектировании и исследовании новых систем, анализе свойств существующих систем, выборе и обосновании оптимальных условий их функционирования и т.п. Изучение математического моделирования открывает широкие возможности для осознания связи информатики с математикой и другими науками. Абстрактное моделирование с помощью компьютеров – вербальное, информационное, математическое – в наши дни стало одной из информационных технологий в познавательном плане исключительно мощной.
Практически во всех науках о природе, живой и неживой, об обществе, построение и использование моделей является мощным орудием познания. Реальные объекты и процессы бывают столь многообразны и сложны, что лучшим способом изучения часто является построение модели, отражающей лишь какую – то часть реальности.
Список использованной литературы 1. Замков О.О., Толстопятенко А.В., Черешных Ю.Н. Математические методы в экономике: Учебник. - М.: МГУ им. М.В.Ломоносова, Издательство «ДИС», 1997. 2. Конспект лекций по предмету «Основы математического моделирования социально-экономических процессов». 3. Минюк С.А. Математические методы и модели в экономике: Учеб. пособие / Минюк С.А., Ровба Е.А., Кузьмич К.К. - Мн.: ТетраСистемс, 2002. 4. Смородинский С.С., Батин Н. В. Оптимизация решений на основе методов и моделей математического программирования. Мн.: БГУИР, 2003. 5. Экономико-математические методы и модели/ Под. ред. А. В. Кузнецова. Мн.: БГЭУ.1999.
|
||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.48.148 (0.009 с.) |

 и точность
и точность  .
. (2.1.4)
(2.1.4) (2.1.5)
(2.1.5) (2.1.6)
(2.1.6) (2.1.7)
(2.1.7) (для поиска max изменить неравенство на
(для поиска max изменить неравенство на  ), то
), то 
 .
. , то
, то  и останавливаемся.
и останавливаемся.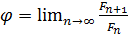 , метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итераций строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.
, метод золотого сечения может быть трансформирован в так называемый метод чисел Фибоначчи. Однако при этом в силу свойств чисел Фибоначчи количество итераций строго ограничено. Это удобно, если сразу задано количество возможных обращений к функции.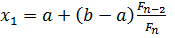 (2.2.1)
(2.2.1) (2.2.2)
(2.2.2) (2.2.3)
(2.2.3) (2.2.4)
(2.2.4)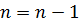
 ,то
,то 

 , то
, то  и останавливаемся.
и останавливаемся.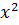 – 20х – 32 на отрезке [ 0; 40 ] за 8 шагов.
– 20х – 32 на отрезке [ 0; 40 ] за 8 шагов. ∙(b - a) = a +
∙(b - a) = a +  ∙(b – a) =
∙(b – a) =  ∙ 40 = 15,2
∙ 40 = 15,2 ∙(b – a) = a +
∙(b – a) = a +  ∙(b – a) =
∙(b – a) =  ∙ 40 = 24,72
∙ 40 = 24,72 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 24,72 = 9,4
∙ 24,72 = 9,4 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 24,72 = 15,4
∙ 24,72 = 15,4 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) = 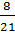 ∙ 15,3 = 5,8
∙ 15,3 = 5,8 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 15,3 = 9,5
∙ 15,3 = 9,5 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 9,5 = 3,61
∙ 9,5 = 3,61 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 9,5 = 5,8
∙ 9,5 = 5,8 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 5,8 = 2,18
∙ 5,8 = 2,18 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 5,8 = 3,63
∙ 5,8 = 3,63 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 3,63 = 1,5
∙ 3,63 = 1,5 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 3,63 = 2,2
∙ 3,63 = 2,2 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 2,2 = 0,726
∙ 2,2 = 0,726 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) =  ∙ 2,2 = 1,47
∙ 2,2 = 1,47 ∙ (b – a) = a +
∙ (b – a) = a + 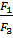 ∙ (b – a) =
∙ (b – a) =  ∙ 1,47 = 0,735
∙ 1,47 = 0,735 ∙ (b – a) = a +
∙ (b – a) = a +  ∙ (b – a) =
∙ (b – a) = 


