
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственный вектор и собственное число линейного оператораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть в пространстве Определение. Ненулевой вектор Из данного определения следует, что образом собственного вектора Отметим некоторые свойства собственных векторов оператора 1. Каждому собственному вектору соответствует единственное собственное число. Предположим обратное: пусть собственному вектору
Но отсюда следует, что
Так как по условию 2. Если
3. Если Действительно,
Таким образом, каждому собственному числу Докажем теорему о существовании собственного вектора. Теорема. В комплексном линейном пространстве Доказательство. Пусть
В координатной форме матричное уравнение (6.3.1) имеет вид
Для отыскания собственного вектора необходимо найти ненулевые решения системы (6.3.2), которые существуют тогда и только тогда, когда определитель системы равен нулю, т.е. когда
Из данной теоремы следует, что нахождение собственного числа линейного оператора Пример. Найти собственные векторы линейного оператора
Решение. Составим характеристическое уравнение
или Подставляем корни При
Получим однородную систему трех линейных уравнений, из которых только одно (любое) является линейно независимым. Общее решение системы имеет вид
Тогда собственные векторы, соответствующие собственным значениям
где с – произвольное действительное число, отличное от нуля. При
Общее решение данной системы имеет вид
Собственный вектор, соответствующий собственному значению
Теорема. Пусть собственные значения Доказательство. Используем метод индукции по числу переменных. Так как Пусть утверждение теоремы справедливо для m<p векторов
Используя свойство линейного оператора, получим
Так как
Умножим (6.3.3) на
По условию все
Следствие: если все собственные значения Теорема. Если в качестве базиса пространства
Доказательство. Рассмотрим произвольный вектор Применяя к вектору Так как Тогда
Из (6.3.7) имеем
Равенства (6.3.8) означают, что матрица линейного оператора
Теорема доказана. Определение. Линейный оператор Очевидно, что операторы простой структуры, и только они, имеют диагональные матрицы в некотором базисе. Этот базис может быть составлен лишь из собственных векторов оператора
6.4. Задания для самостоятельной работы по главе 6
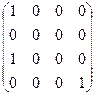
6.1.–6.10. Найти собственные значения и собственные векторы линейных преобразований, заданных в некотором базисе матрицами:
6.11. Доказать, что собственные векторы линейного преобразования, принадлежащие различным собственным значениям, линейно независимы.
6.12. Пусть
6.13. Пусть
6.14. Найти собственные значения и собственные векторы линейного преобразования, являющегося дифференцированием многочленов степени
6.15. Даны векторы
где
Найти связь между новым и старым базисом. Найти координаты вектора Глава 7. Квадратичные формы
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 446; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.116.31 (0.012 с.) |

 задан линейный оператор
задан линейный оператор  .
. , удовлетворяющий соотношению
, удовлетворяющий соотношению  , называется собственным вектором, а соответствующее число
, называется собственным вектором, а соответствующее число  – собственным значением оператора
– собственным значением оператора 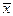 является коллинеарный ему вектор
является коллинеарный ему вектор  .
. . Это значит, что
. Это значит, что ,
, .
.
 .
.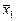 и
и  – собственные векторы оператора
– собственные векторы оператора  также является собственным вектором оператора
также является собственным вектором оператора 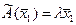 и
и  , то
, то .
. , коллинеарный вектору
, коллинеарный вектору  .
. и обозначим координаты вектора
и обозначим координаты вектора  в этом базисе через
в этом базисе через  . Тогда, если
. Тогда, если 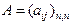 – матрица оператора
– матрица оператора  где
где  .
.

 . Отсюда следует, что собственное число линейного оператора
. Отсюда следует, что собственное число линейного оператора  – различные корни характеристического уравнения. Подставив какой-нибудь корень
– различные корни характеристического уравнения. Подставив какой-нибудь корень  в систему (6.3.2), найдем все ее линейно независимые решения, которые и определяют собственные векторы, соответствующие собственному числу
в систему (6.3.2), найдем все ее линейно независимые решения, которые и определяют собственные векторы, соответствующие собственному числу  равен r и r<n, то существует k=n-r линейно независимых собственных векторов, отвечающих корню.
равен r и r<n, то существует k=n-r линейно независимых собственных векторов, отвечающих корню. .
. ,
, откуда
откуда  .
.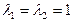 имеем
имеем
 .
.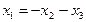 . Найдем два линейно независимых решения:
. Найдем два линейно независимых решения: .
. ,
, имеем
имеем .
.
 .
. оператора
оператора  линейно независимы.
линейно независимы. . Присоединим к этим векторам вектор
. Присоединим к этим векторам вектор  и допустим, что имеет место равенство
и допустим, что имеет место равенство

 , -собственные векторы, то
, -собственные векторы, то  и поэтому равенство (6.3.4) можно переписать следующим образом:
и поэтому равенство (6.3.4) можно переписать следующим образом:
 и вычтем из (6.3.5), получим
и вычтем из (6.3.5), получим
 , различны, поэтому
, различны, поэтому  . Система векторов
. Система векторов  . Тогда из (6.3.3) и из условия, что
. Тогда из (6.3.3) и из условия, что 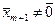 ), получаем
), получаем  . Это означает, что
. Это означает, что  – система линейно независимых векторов. Индукция проведена. Теорема доказана.
– система линейно независимых векторов. Индукция проведена. Теорема доказана. попарно различны, то отвечающие им собственные векторы
попарно различны, то отвечающие им собственные векторы  образуют базис пространства
образуют базис пространства  .
. и базис, составленный из собственных векторов
и базис, составленный из собственных векторов  этого пространства. Тогда
этого пространства. Тогда  , где
, где  – координаты вектора
– координаты вектора  в базисе
в базисе  или
или  .
. , – собственный вектор, то
, – собственный вектор, то  .
.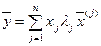
 ,
,
 ,
…………
,
…………
 .
.









 , принадлежащий собственному значению
, принадлежащий собственному значению  – функция, для которой преобразование
– функция, для которой преобразование  имеет смысл (если
имеет смысл (если  , причем можно доказать, что
, причем можно доказать, что  .
. следует
следует  .
. с вещественными коэффициентами.
с вещественными коэффициентами.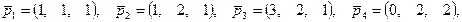
 образуют новый базис, в базисе
образуют новый базис, в базисе
 в новом базисе.
в новом базисе.


