
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Собственные векторы и собственные значенияСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Вектор
Число Из данного определения следует схема получения
В развернутом виде получим однородную систему:
которая называется характеристической, и будет иметь ненулевое решение, если ее определитель обращается в нуль:
Уравнение (21) называется характеристическим (или вековым) и служит для получения собственных значений
где Пусть уравнение (22) имеет три действительных корня
причем диагональную, по главной диагонали которой стоят собственные значения
Это справедливо только для случая различных действительных корней. Предлагаем студентам проверить это самостоятельно. Замечание. Если матрица линейного оператора симметрическая Предлагаем студентам проверить это самостоятельно.
Пример 14 Найти собственные векторы и собственные значения линейного оператора, заданного в некотором базисе симметрической матрицей
Решение Искомый собственный вектор
Собственные значения После раскрытия определителя получаем алгебраическое уравнение 3-й степени:
Приходим к уравнению вида:
Получаем собственные значения Строим собственные векторы. Значение
Ее определитель равен нулю, и, следовательно, ранг системы
По правилу Крамера Аналогично значение
Вновь система равносильна двум уравнениям:
Получаем координаты второго собственного вектора: Далее берем
Ответ: Заметим, что построенные векторы Собственные векторы можно нормировать:
Показать, что матрица линейного оператора в базисе из собственных векторов будет иметь диагональную форму:
Приведение квадратичной формы к каноническому виду
Пусть задана квадратичная форма от двух переменных вида:
Значит, матрица квадратичной формы
Пример 15 Для т.е. Матрица квадратичной формы в базисе из собственных векторов будет диагональной, т.е. Действительно, составим характеристическую систему
Ее определитель равен нулю:
Получим характеристическое уравнение
Решим систему при
Полагаем Аналогично, для
Полагаем Заметим, что Строим матрицу перехода Обратная матрица существует:
Тогда квадратичная форма в базисе из собственных векторов примет канонический вид:
При этом «новые»
Замечание. Аналогично для квадратичной формы от 3-х переменных
. Матрица (квадратичной формы)
Например, т. к. В базисе из собственных векторов квадратичная форма примет вид:
Замечание об евклидовых пространствах В линейном
Такая операция над векторами обладает следующими свойствами: 1) 2) 3) 4)
Длиной (нормой) вектора
для которой выполняются свойства: 1) 2) 3) 4) Угол
Определение корректно, т.к. согласно неравенству Коши–Буняковского
Два вектора называется ортогональными, если Векторы Теорема 4. Во всяком Например, в
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.140 (0.01 с.) |

 называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  , если действие этого оператора на
, если действие этого оператора на  сводится к растяжению вектора в
сводится к растяжению вектора в  раз, т.е.
раз, т.е. .
.
 и
и  . Перепишем
. Перепишем  или
или  и так как
и так как  .
.



 – след матрицы
– след матрицы  – алгебраические дополнения,
– алгебраические дополнения,  – определитель матрицы
– определитель матрицы  . Тогда из системы (20) находим координаты собственных векторов
. Тогда из системы (20) находим координаты собственных векторов  . Составим матрицу
. Составим матрицу  , по столбцам которой стоят координаты этих векторов. Это матрица перехода от стандартного базиса
, по столбцам которой стоят координаты этих векторов. Это матрица перехода от стандартного базиса  к базису из собственных векторов и тогда линейный оператор
к базису из собственных векторов и тогда линейный оператор  ,
,
 , т.е.
, т.е. .
. , то ее собственные значения действительные и различные, а собственные векторы ортогональны.
, то ее собственные значения действительные и различные, а собственные векторы ортогональны. .
. удовлетворяет характеристической системе
удовлетворяет характеристической системе
 .
.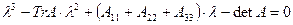 , где
, где  ,
, ,
,  ,
,  ,
, .
.
 – все действительные и различные.
– все действительные и различные. подставляем в характеристическую систему:
подставляем в характеристическую систему:
 (т.к. минор
(т.к. минор  ). Система равносильна системе:
). Система равносильна системе: или
или 
 ,
,  ,
,  .
. . Полагаем
. Полагаем  и получаем 1-й собственный вектор
и получаем 1-й собственный вектор  . Можно взять
. Можно взять  и тогда
и тогда  .
. подставляем в характеристическую систему:
подставляем в характеристическую систему:
 т. к. минор
т. к. минор  и
и  по формулам Крамера:
по формулам Крамера: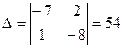 ;
;  ;
;  .
. . Полагаем
. Полагаем  и
и  ,
,  . Можно взять
. Можно взять  и тогда
и тогда  .
. и подставляем в характеристическую систему:
и подставляем в характеристическую систему:
 ,
,  ,
, 
 . Получим 3-й собственный вектор
. Получим 3-й собственный вектор  . Можно взять
. Можно взять  , тогда
, тогда  .
. ,
,  ,
,  .
. ,
,  ,
,  .
. ,
,  ,
,  – эти три вектора образуют ортонормированный базис в 3-х мерном пространстве.
– эти три вектора образуют ортонормированный базис в 3-х мерном пространстве. .
. , где
, где  или
или
 .
.
 является симметрической.
является симметрической. ,
, .
. .
.
 или
или , где
, где  ,
,  .
. , корни которого
, корни которого ,
,  .
. :
: или
или  .
.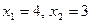 и получаем 1-й собственный вектор
и получаем 1-й собственный вектор  .
.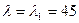 :
: или
или  .
. и получаем 2-й собственный вектор
и получаем 2-й собственный вектор  .
.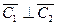 , т. к.
, т. к.  .
. , ее определитель
, ее определитель  .
. , и в базисе из собственных векторов
, и в базисе из собственных векторов  получаем вид матрицы квадратной формы:
получаем вид матрицы квадратной формы:
 .
. или
или  .
. и «старые» координаты
и «старые» координаты  связаны между собой формулой
связаны между собой формулой или
или 
 , где
, где 



 ,
, .
. , где
, где  –мерном пространстве вводим скалярное произведение по правилу:
–мерном пространстве вводим скалярное произведение по правилу: .
.
 – коммутативность;
– коммутативность; – дистрибутивность;
– дистрибутивность; – ассоциативность по умножению на скаляр;
– ассоциативность по умножению на скаляр; при
при  и
и  при
при  .
. ,
,
 , если
, если  ;
; при любом
при любом  ;
; – неравенство Коши–Буняковского;
– неравенство Коши–Буняковского; – неравенство треугольника.
– неравенство треугольника. между векторами
между векторами  в евклидовом пространстве определяется из формулы:
в евклидовом пространстве определяется из формулы: , где
, где  .
.
 .
. , откуда
, откуда  .
.
 пространства образуют ортонормированный базис, если
пространства образуют ортонормированный базис, если  при любых
при любых  и
и  при
при  .
. :
:  ,
,  ,
,  .
.


