
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Решение квадратных систем линейных алгебраических уравнений (СЛАУ) матричным методом и по правилу Крамера
Пусть задана система вида:
Запишем квадратную матрицу системы размерности
В этих обозначениях система (11) примет вид:
Если
Заметим, что Решение:
Тем самым мы получили формулы Крамера:
для СЛАУ (11), где главный определитель системы
Теорема 1 (Крамера). СЛАУ (11) можно привести к виду:
Тогда возможны три случая: 1. Если главный определитель
2. Если 3. Если
1.7. Метод Гаусса Для систем произвольного вида
(прямоугольных), где число уравнений не совпадает с числом неизвестных, применяется общий метод последовательного исключения (МПИ) неизвестных, основанный на элементарных преобразованиях типа: 1) умножение некоторого уравнения системы на отличное от нуля число; 2) прибавление к одному уравнению системы другого ее уравнения, умноженного на произвольное число, отличное от нуля; 3) перестановка местами двух уравнений системы. Такие преобразования системы не изменяют множество ее решений и называются преобразованиями типа Гаусса. Заметим, что, выполняя преобразования 1–3 над уравнениями системы, соответствующие элементарные преобразования производятся над строками расширенной матрицы системы:
Поэтому на практике экономичней проводить МПИ в матричной форме. После конечного числа шагов элементарных преобразований приходим к матрицам вида:
В случае а) система примет треугольную форму и будет иметь единственное решение, а в случае б) система примет трапециевидную форму Заметим, что если на некотором шаге появится строка
Нахождение неизвестных
Метод Жордановых исключений
В основе метода Жордановых исключений лежат элементарные преобразования типа Гаусса, с помощью которых приводим матрицу системы к единичной
Автоматически получим решение СЛАУ:
При решении СЛАУ методом Жордановых исключений удобно расширенную матрицу системы записывать в виде следующей таблицы:
1.9. Ранг матрицы. Теорема Кронекера – Капелли
Наивысший порядок отличных от нуля миноров матрицы
Находим ее окаймляющие миноры:
Окаймляющий минор 3-го порядка равен нулю, следовательно ранг равен порядку предыдущего минора Замечание. Минор Рассмотрим произвольную систему вида (16) Основная матрица этой системы
Это и есть теорема Кронекера–Капелли. Для ранга системы возможны два случая: 1) если общий ранг равен числу неизвестных 2) если Если же
Пример 11 Выяснить совместность системы и найти ее решение.
Решение Система является переопределенной: число уравнений
Методом окаймляющих миноров найдем ранги этих матриц:
Так как основная матрица
Для расширенной матрицы считаем окаймляющий минор:
Следовательно, ранг расширенной матрицы Найдем это решение методом Жордановых исключений:
~ Ответ: система имеет единственное решение
1.10. Однородные системы
где 1) однородная система будет иметь ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных; 2) если в однородной системе число уравнений меньше числа неизвестных, то система имеет ненулевое решение; 3) однородная система, в которой число уравнений равно числу неизвестных, имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю; 4) пусть наборы Из числа решений однородной системы (17) всегда можно построить конечную линейно независимую систему решений, причем такую, что всякое другое решение системы (17) будет линейной комбинацией решений, входящих в эту построенную систему. Такую систему решений называют фундаментальной.
Теорема 2. Если ранг
Пример 12 Построить фундаментальную систему решений однородной системы линейных уравнений:
Решение Выясним ранг системы, т.е. запишем матрицу
Следовательно, ранг системы равен 2, т.е.
По формуле Крамера находим
Получаем решение исходной однородной системы в виде
Все решения однородной системы получаются как линейная комбинация: Замечание. Геометрически полученное решение в 4-х мерном пространстве изображается 2-х мерной плоскостью, т.к. ее параметрические уравнения имеют вид:
II. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
2.1. n – мерные векторные пространства
Упорядоченная совокупность
Операции над Пусть 1) 2) Операции 1–2 называются линейными и удовлетворяют следующим свойствам: 1) 2) 3) 4) существует нуль–вектор 5) для любого
Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее свойствам 1–5, называется векторным пространством. Если под Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов, т.е. Замечание. Векторы
В противном случае векторы Любой вектор Пусть заданы два базиса:
Найдем связь «старых» и «новых» координат вектора
и подставим в
Отсюда замечаем, что матрица, по столбцам которой стоят координаты базисных векторов Обозначим ее через
Линейные операторы
Если указано правило, по которому вектору
Он обладает свойствами: 1) 2) и называется линейным оператором. При этом вектор 1) 2) 3) 4) существует нулевой оператор 5) существует тождественный оператор
Если
Теорема 3. Матрицы
где
Доказать теорему самостоятельно.
Пример 13 В базисе Решение Составим матрицу
Тогда по формуле
Ответ: матрица линейного оператора в «новом» базисе имеет вид
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 281; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.185.123 (0.113 с.) |

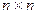 :
: , матрицу-столбец из неизвестных
, матрицу-столбец из неизвестных 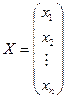 , и матрицу-столбец из свободных коэффициентов
, и матрицу-столбец из свободных коэффициентов  .
. .
.
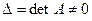 , то решение матричного уравнения (12) следующее:
, то решение матричного уравнения (12) следующее: .
.
 , т.е.
, т.е.  – матрица такой же размерности, что и
– матрица такой же размерности, что и  . Формула для обратной матрицы
. Формула для обратной матрицы  .
. .
.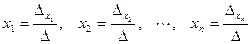 .
.
 – вспомогательные определители (получающиеся из главного заменой
– вспомогательные определители (получающиеся из главного заменой  -го столбца на столбец из свободных коэффициентов). Например
-го столбца на столбец из свободных коэффициентов). Например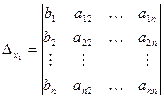 можно обозначить
можно обозначить  .
. .
.
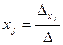 , где
, где 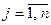 .
. , а хотя бы один
, а хотя бы один  , то система не совместна (решений не имеет), поскольку имеется противоречивое уравнение
, то система не совместна (решений не имеет), поскольку имеется противоречивое уравнение 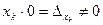 .
.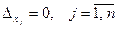 , то система имеет бесконечное число решений.
, то система имеет бесконечное число решений.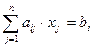 , где
, где 
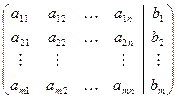 .
.
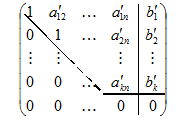
 и будет иметь множество решений.
и будет иметь множество решений.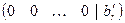 ,
,  , то система будет несовместной, т.е. не будет иметь решений.
, то система будет несовместной, т.е. не будет иметь решений. из преобразованной (треугольной или трапецевидной) системы идет снизу вверх и называется обратным ходом в методе Гаусса.
из преобразованной (треугольной или трапецевидной) системы идет снизу вверх и называется обратным ходом в методе Гаусса. . Тогда расширенная матрица СЛАУ
. Тогда расширенная матрица СЛАУ .
.
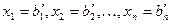 (см. пример 11).
(см. пример 11).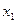












 называется рангом этой матрицы и обозначается
называется рангом этой матрицы и обозначается  . Для вычисления ранга матрицы применяем метод окаймляющих миноров.
. Для вычисления ранга матрицы применяем метод окаймляющих миноров.

 ;
; 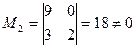 ;
;  .
. , т. е.
, т. е.  .
. порядка
порядка  , содержащий в себе минор
, содержащий в себе минор  порядка
порядка  , называется окаймляющим минором
, называется окаймляющим минором  , а все окаймляющие его миноры
, а все окаймляющие его миноры  , то
, то  .
.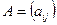 , а расширенная
, а расширенная  , где
, где 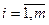 ,
,  . Система (16) будет совместной (т.е. будет иметь решение) тогда и только тогда, когда ранг матрицы системы совпадает с рангом расширенной матрицы этой системы, т.е.
. Система (16) будет совместной (т.е. будет иметь решение) тогда и только тогда, когда ранг матрицы системы совпадает с рангом расширенной матрицы этой системы, т.е. .
.
 , то система (16) будет иметь единственное решение;
, то система (16) будет иметь единственное решение; , то система (16) будет иметь бесконечное число решений.
, то система (16) будет иметь бесконечное число решений. , то система (16) несовместна, т.е. не имеет решений.
, то система (16) несовместна, т.е. не имеет решений.
 больше числа неизвестных
больше числа неизвестных  . Запишем основную
. Запишем основную  матрицы системы:
матрицы системы:

 ,
,  ,
,  .
. .
. .
. . Тогда, по теореме Кронекера–Капелли, исходная система имеет единственное решение, т.к.
. Тогда, по теореме Кронекера–Капелли, исходная система имеет единственное решение, т.к. 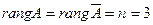 .
.






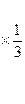

 ~
~
 ~
~ 
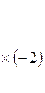 + ~
+ ~  – + ~
– + ~ 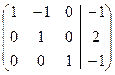
 ~
~

 .
. ,
,
 удовлетворяет всем уравнениям системы. Это решение называется тривиальным, в остальных случаях:
удовлетворяет всем уравнениям системы. Это решение называется тривиальным, в остальных случаях: и
и  являются решениями однородной системы, тогда их линейная комбинация
являются решениями однородной системы, тогда их линейная комбинация  – также решение однородной системы (17).
– также решение однородной системы (17). решений.
решений.

 ;
;  ;
; ;
;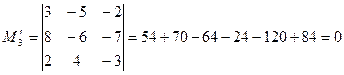 .
. . А значит, система имеет ненулевые решения и, по теореме 2 фундаментальная система решений будет состоять из
. А значит, система имеет ненулевые решения и, по теореме 2 фундаментальная система решений будет состоять из  линейно независимых решений. При этом базисный минор
линейно независимых решений. При этом базисный минор  где
где  и
и  – свободными, принимающими любые действительные значения.
– свободными, принимающими любые действительные значения. и
и  , где
, где  ,
, ,
,  .
. ;
;  , где
, где  . Полагаем для свободных переменных
. Полагаем для свободных переменных  и
и  и находим 2 линейно независимых решения:
и находим 2 линейно независимых решения:  и
и  .
.

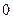


 ;
;  – любые действительные числа.
– любые действительные числа. ,
,  ,
,  .
. действительных чисел, записанных в виде
действительных чисел, записанных в виде  -я компонента. Два
-я компонента. Два  и
и  равны тогда и только тогда, когда равны их соответствующие компоненты:
равны тогда и только тогда, когда равны их соответствующие компоненты:  .
. – сложение векторов;
– сложение векторов; – умножение вектора на число.
– умножение вектора на число. – коммутативность;
– коммутативность; – ассоциативность;
– ассоциативность; – дистрибутивность;
– дистрибутивность; такой, что
такой, что  ;
; , такой, что
, такой, что 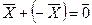 .
. рассматривать объекты любой природы (например алгебраические многочлены степени не выше
рассматривать объекты любой природы (например алгебраические многочлены степени не выше  называется
называется  векторов уже линейно зависимы.
векторов уже линейно зависимы. . Совокупность
. Совокупность  пространства
пространства  , неравные одновременно нулю, что
, неравные одновременно нулю, что .
.
 .
. можно представить и при том единственным способом в виде линейной комбинации векторов базиса. Пусть
можно представить и при том единственным способом в виде линейной комбинации векторов базиса. Пусть  образуют базис в
образуют базис в 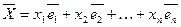 называется разложением вектора
называется разложением вектора  – «старый» и
– «старый» и 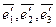 – «новый». Разложим вектор
– «новый». Разложим вектор  ,
, .
.
 Из равенства векторов получим:
Из равенства векторов получим:
 .
. и получим замену «старых» координат «новыми»:
и получим замену «старых» координат «новыми»: , где
, где 
 . Обратно, замена «новых» на «старые» координаты будет осуществляться с помощью обратной матрицы:
. Обратно, замена «новых» на «старые» координаты будет осуществляться с помощью обратной матрицы: 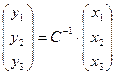 .
. ставится в соответствие единственный вектор
ставится в соответствие единственный вектор  , то говорят, что задан оператор
, то говорят, что задан оператор  .
.
 – аддитивность;
– аддитивность; – однородность,
– однородность, ,
,  ;
; ;
; ;
; ;
; , такой, что
, такой, что  .
. и
и  , то
, то  , где
, где 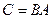 . Действительно,
. Действительно,  и
и  . Это есть свойство транзитивности линейного оператора.
. Это есть свойство транзитивности линейного оператора. и
и 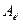 линейного оператора в базисах
линейного оператора в базисах  ,
,
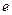 к «новому» базису
к «новому» базису 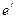 .
. линейный оператор задан матрицей
линейный оператор задан матрицей  . Найти матрицу оператора в базисе
. Найти матрицу оператора в базисе  .
.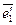 и
и  :
: .
. получим вид матрицы
получим вид матрицы 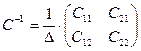 , где
, где 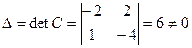 . Алгебраические дополнения:
. Алгебраические дополнения: 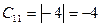 ,
,  ,
, 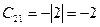 ,
,  , отсюда
, отсюда  . Находим
. Находим 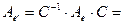
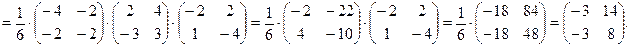
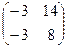 .
.


