
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Введение в линейную алгебру. Краткий обзорСодержание книги Поиск на нашем сайте
I. ВВЕДЕНИЕ В ЛИНЕЙНУЮ АЛГЕБРУ. КРАТКИЙ ОБЗОР
Матрицы. Начальные сведения
Рассматриваем новый математический объект – матрицу. Это абстрактная таблица, состоящая из
где Если число строк равно числу столбцов, то матрица называется квадратной. Например, Элементы
Если вне главной диагонали стоят нулевые элементы, то матрица называется диагональной, например
Матрица, состоящая только из нулевых элементов, называется нулевой матрицей: Если элементы матрицы, стоящие на симметричных местах относительно главной диагонали совпадают:
Матрица вида
Операции над матрицами
Сложение матриц и умножение матрицы на число называются линейными операциями. Они выполняются по следующим правилам: 1. 2.
Пример 1
3. Умножение матриц выполняется по следующей схеме:
Заметим, что в левой матрице число столбцов совпадает с числом строк в правой матрице. Только в этом случае операция умножения возможна.
Пример 2
Пример 3
Замечание. В общем случае умножение матриц неперестановочно, т.е.
Пример 4
4. Матрицы можно возводить в степень, причем только квадратные, т.е. число столбцов должно соответствовать числу строк.
5. Рассмотрим еще одну операцию над матрицами – транспонирование. При транспонировании матрицы
Пример 5
Определители квадратных матриц
Прежде чем ввести операцию обращения матриц
Таким образом,
Пример 6
Однако для матрицы размера 3×3 определитель строится сложнее:
Для простоты запоминания пользуются следующими схемами:
Схема называется правилом треугольников. Модифицируем его, т.е. распрямим треугольники.
Если квадратная матрица имеет размер 4×4 и выше, то для вычисления ее определителя применяется правило Лапласа:
т.е. детерминант матрицы При этом Заметим, что правило Лапласа позволяет определители
Пример 7
Замечание. Если определитель матрицы приведен к треугольному виду
то его значение равно произведению элементов, стоящих по главной диагонали, т.е. Отметим элементарные преобразования (Э.П.) над строками определителя, которые не меняют его значения: 1) вынесение общего множителя строки за знак определителя; 2) прибавление к одной строке элементов другой строки; 3) прибавление к одной строке элементов другой, умноженных на некоторое число.
Пример 8
Замечание 1. Такие же Э.П. можно выполнять и над столбцами определителя. Замечание 2. Определитель и называется определителем Вандермонда. Студентам предлагается доказать это самостоятельно.
Нахождение обратной матрицы
Теперь можно перейти к обращению квадратных матриц. В этом случае
где
поскольку
Замечание. Обратную матрицу можно построить с помощью элементарных преобразований по следующей схеме:
Пример 9 С помощью элементарных преобразований провести обращение матрицы
Решение
~ Действительно,
Решение матричных уравнений
Пусть задано уравнение
где матрица
при этом
Пример 10 Решить матричное уравнение
Решение Имеем уравнение Вычислим алгебраические дополнения матрицы
Таким образом, Сделаем проверку: Искомое решение: Проверить, что
Метод Жордановых исключений
В основе метода Жордановых исключений лежат элементарные преобразования типа Гаусса, с помощью которых приводим матрицу системы к единичной
Автоматически получим решение СЛАУ:
При решении СЛАУ методом Жордановых исключений удобно расширенную матрицу системы записывать в виде следующей таблицы:
1.9. Ранг матрицы. Теорема Кронекера – Капелли
Наивысший порядок отличных от нуля миноров матрицы
Находим ее окаймляющие миноры:
Окаймляющий минор 3-го порядка равен нулю, следовательно ранг равен порядку предыдущего минора Замечание. Минор Рассмотрим произвольную систему вида (16) Основная матрица этой системы
Это и есть теорема Кронекера–Капелли. Для ранга системы возможны два случая: 1) если общий ранг равен числу неизвестных 2) если Если же
Пример 11 Выяснить совместность системы и найти ее решение.
Решение Система является переопределенной: число уравнений
Методом окаймляющих миноров найдем ранги этих матриц:
Так как основная матрица Для расширенной матрицы считаем окаймляющий минор:
Следовательно, ранг расширенной матрицы Найдем это решение методом Жордановых исключений:
~ Ответ: система имеет единственное решение
1.10. Однородные системы
где 1) однородная система будет иметь ненулевое решение тогда и только тогда, когда ее ранг меньше числа неизвестных; 2) если в однородной системе число уравнений меньше числа неизвестных, то система имеет ненулевое решение; 3) однородная система, в которой число уравнений равно числу неизвестных, имеет ненулевое решение тогда и только тогда, когда ее определитель равен нулю; 4) пусть наборы Из числа решений однородной системы (17) всегда можно построить конечную линейно независимую систему решений, причем такую, что всякое другое решение системы (17) будет линейной комбинацией решений, входящих в эту построенную систему. Такую систему решений называют фундаментальной.
Теорема 2. Если ранг
Пример 12 Построить фундаментальную систему решений однородной системы линейных уравнений:
Решение Выясним ранг системы, т.е. запишем матрицу
Следовательно, ранг системы равен 2, т.е.
По формуле Крамера находим
Получаем решение исходной однородной системы в виде
Все решения однородной системы получаются как линейная комбинация: Замечание. Геометрически полученное решение в 4-х мерном пространстве изображается 2-х мерной плоскостью, т.к. ее параметрические уравнения имеют вид:
II. ЛИНЕЙНЫЕ ПРОСТРАНСТВА
2.1. n – мерные векторные пространства
Упорядоченная совокупность
Операции над Пусть 1) 2) Операции 1–2 называются линейными и удовлетворяют следующим свойствам: 1) 2) 3) 4) существует нуль–вектор 5) для любого Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее свойствам 1–5, называется векторным пространством. Если под Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов, т.е. Замечание. Векторы
В противном случае векторы Любой вектор Пусть заданы два базиса:
Найдем связь «старых» и «новых» координат вектора
и подставим в
Отсюда замечаем, что матрица, по столбцам которой стоят координаты базисных векторов Обозначим ее через
Линейные операторы
Если указано правило, по которому вектору
Он обладает свойствами: 1) 2) и называется линейным оператором. При этом вектор 1) 2) 3) 4) существует нулевой оператор 5) существует тождественный оператор Если
Теорема 3. Матрицы
где
Доказать теорему самостоятельно.
Пример 13 В базисе Решение Составим матрицу
Тогда по формуле
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 231; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.19.89 (0.015 с.) |

 строк и
строк и  столбцов вида:
столбцов вида: ,
,
 – элементы матрицы, стоящие на пересечении
– элементы матрицы, стоящие на пересечении  -ой строки и
-ой строки и  -го столбца. Элементы
-го столбца. Элементы  имеет размерность
имеет размерность  , и кратко записывают
, и кратко записывают 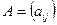 , где
, где 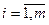 ,
,  .
. – прямоугольная, а
– прямоугольная, а  – квадратная матрица.
– квадратная матрица. ,
,  ,
,  ,…,
,…,  образуют главную диагональ в матрице
образуют главную диагональ в матрице 

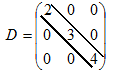


 , то такая матрица называется симметрической.
, то такая матрица называется симметрической.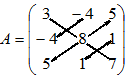
 называется матрицей-строкой, а матрица вида называется
называется матрицей-строкой, а матрица вида называется  – матрицей-столбцом.
– матрицей-столбцом. , где
, где  .
. , где
, где  .
. .
. , где
, где  .
.

 . Однако, можно подобрать две квадратные матрицы, чтобы
. Однако, можно подобрать две квадратные матрицы, чтобы  , в этом случае говорят, что матрицы коммутируют.
, в этом случае говорят, что матрицы коммутируют. ,
,  ,
, ;
; .
. или
или  . Транспонировать можно матрицы любой размерности.
. Транспонировать можно матрицы любой размерности.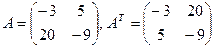 .
. , необходимо дать понятие определителя квадратной матрицы. Для квадратной матрицы размера 2×2 определителем является число Δ, получающееся по формуле
, необходимо дать понятие определителя квадратной матрицы. Для квадратной матрицы размера 2×2 определителем является число Δ, получающееся по формуле
 , где
, где  – первые три буквы от латинского determinantis (определитель). Так легко получается детерминант 2-го порядка.
– первые три буквы от латинского determinantis (определитель). Так легко получается детерминант 2-го порядка. .
.




 где:
где:  ,
,
 – минор (определитель
– минор (определитель  -го порядка), получающийся из матрицы
-го порядка), получающийся из матрицы  – алгебраическое дополнение к элементу
– алгебраическое дополнение к элементу 
 ,
, . Это автоматически следует из правила Лапласа.
. Это автоматически следует из правила Лапласа.




 + =
+ =


 +
+ 

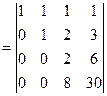




 должен быть отличным от нуля, и матрица
должен быть отличным от нуля, и матрица 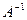 , причем
, причем  дает единичную матрицу. Легко показать, что обратная матрица имеет вид:
дает единичную матрицу. Легко показать, что обратная матрица имеет вид: ,
,

 Предлагаем студентам самостоятельно это проверить.
Предлагаем студентам самостоятельно это проверить. .
.
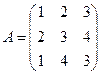 .
.


 + – ~
+ – ~ 
 + ~
+ ~ ~
~ 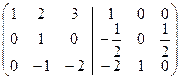 + ~
+ ~ 
 ~
~
 ~
~ 
 + ~
+ ~ 
 + ~
+ ~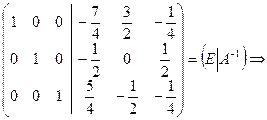
 .
. .
. ,
,
 . Тогда умножим слева заданное равенство на
. Тогда умножим слева заданное равенство на  или
или
 есть
есть  , то искомая матрица
, то искомая матрица  имеет такую же размерность, что и
имеет такую же размерность, что и 



 .
.
 .
. , где
, где  ,
,  . Находим
. Находим  , тогда
, тогда  .
.
 .
. .
. .
. дает матрицу
дает матрицу  . Тогда расширенная матрица СЛАУ
. Тогда расширенная матрица СЛАУ .
.
 (см. пример 11).
(см. пример 11).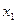











 . Для вычисления ранга матрицы применяем метод окаймляющих миноров.
. Для вычисления ранга матрицы применяем метод окаймляющих миноров.
 ;
; 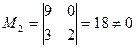 ;
;  .
. , т. е.
, т. е.  .
. порядка
порядка  , содержащий в себе минор
, содержащий в себе минор  порядка
порядка  , называется окаймляющим минором
, называется окаймляющим минором  , а все окаймляющие его миноры
, а все окаймляющие его миноры  , то
, то  .
. , где
, где  .
.
 , то система (16) будет иметь единственное решение;
, то система (16) будет иметь единственное решение; , то система (16) будет иметь бесконечное число решений.
, то система (16) будет иметь бесконечное число решений. , то система (16) несовместна, т.е. не имеет решений.
, то система (16) несовместна, т.е. не имеет решений.
 больше числа неизвестных
больше числа неизвестных  . Запишем основную
. Запишем основную  матрицы системы:
матрицы системы:

 ,
,  ,
,  .
. .
. .
. . Тогда, по теореме Кронекера–Капелли, исходная система имеет единственное решение, т.к.
. Тогда, по теореме Кронекера–Капелли, исходная система имеет единственное решение, т.к. 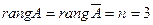 .
.




 ~
~
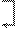
 ~
~ 
 + ~
+ ~  – + ~
– + ~ 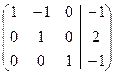
 ~
~

 .
. ,
,
 удовлетворяет всем уравнениям системы. Это решение называется тривиальным, в остальных случаях:
удовлетворяет всем уравнениям системы. Это решение называется тривиальным, в остальных случаях: и
и  являются решениями однородной системы, тогда их линейная комбинация
являются решениями однородной системы, тогда их линейная комбинация  – также решение однородной системы (17).
– также решение однородной системы (17). решений.
решений.

 ;
;  ;
; ;
;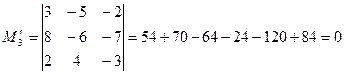 .
. . А значит, система имеет ненулевые решения и, по теореме 2 фундаментальная система решений будет состоять из
. А значит, система имеет ненулевые решения и, по теореме 2 фундаментальная система решений будет состоять из  линейно независимых решений. При этом базисный минор
линейно независимых решений. При этом базисный минор  где
где  и
и  – свободными, принимающими любые действительные значения.
– свободными, принимающими любые действительные значения. и
и  , где
, где  ,
, ,
,  .
. ;
;  , где
, где  . Полагаем для свободных переменных
. Полагаем для свободных переменных  и
и  и находим 2 линейно независимых решения:
и находим 2 линейно независимых решения:  и
и  .
.

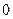


 ;
;  – любые действительные числа.
– любые действительные числа. ,
,  ,
,  .
. -я компонента. Два
-я компонента. Два  и
и  равны тогда и только тогда, когда равны их соответствующие компоненты:
равны тогда и только тогда, когда равны их соответствующие компоненты:  .
. – сложение векторов;
– сложение векторов; – умножение вектора на число.
– умножение вектора на число. – коммутативность;
– коммутативность; – ассоциативность;
– ассоциативность; – дистрибутивность;
– дистрибутивность; такой, что
такой, что  ;
; , такой, что
, такой, что 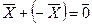 .
. рассматривать объекты любой природы (например алгебраические многочлены степени не выше
рассматривать объекты любой природы (например алгебраические многочлены степени не выше  называется
называется  векторов уже линейно зависимы.
векторов уже линейно зависимы. . Совокупность
. Совокупность  пространства
пространства  , неравные одновременно нулю, что
, неравные одновременно нулю, что .
.
 .
. можно представить и при том единственным способом в виде линейной комбинации векторов базиса. Пусть
можно представить и при том единственным способом в виде линейной комбинации векторов базиса. Пусть  образуют базис в
образуют базис в 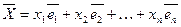 называется разложением вектора
называется разложением вектора  – координаты вектора относительно этого базиса.
– координаты вектора относительно этого базиса. – «старый» и
– «старый» и 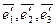 – «новый». Разложим вектор
– «новый». Разложим вектор  ,
, .
.
 Из равенства векторов получим:
Из равенства векторов получим:
 .
. и получим замену «старых» координат «новыми»:
и получим замену «старых» координат «новыми»: , где
, где 
 . Обратно, замена «новых» на «старые» координаты будет осуществляться с помощью обратной матрицы:
. Обратно, замена «новых» на «старые» координаты будет осуществляться с помощью обратной матрицы: 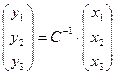 .
. ставится в соответствие единственный вектор
ставится в соответствие единственный вектор  , то говорят, что задан оператор
, то говорят, что задан оператор  .
.
 – аддитивность;
– аддитивность; – однородность,
– однородность, ,
,  ;
; ;
; ;
; ;
;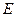 , такой, что
, такой, что  .
.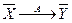 и
и  , то
, то  , где
, где 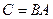 . Действительно,
. Действительно,  и
и  . Это есть свойство транзитивности линейного оператора.
. Это есть свойство транзитивности линейного оператора. и
и 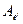 линейного оператора в базисах
линейного оператора в базисах  ,
,
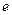 к «новому» базису
к «новому» базису  .
. линейный оператор задан матрицей
линейный оператор задан матрицей  . Найти матрицу оператора в базисе
. Найти матрицу оператора в базисе  .
.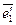 и
и  :
: .
. получим вид матрицы
получим вид матрицы 


