
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость и вогнутость графика функции. Точки перегибаСодержание книги
Поиск на нашем сайте
Определение. График функции Определение. График функции Определение. Точки, в которых график функции переходит с одной стороны своей касательной на другую, то есть пересекает свою касательную, называют точками перегиба (рис. 8).
Рис. 6. Рис. 7.
Рис. 8. Теорема. Достаточный признак выпуклости или вогнутости функции Из достаточного признака выпуклости и вогнутости графика функции получаем необходимый признак наличия точек перегиба: в точке перегиба вторая производная функции либо равна нулю, либо не существует. Теорема. Достаточный признак наличия или отсутствия точки перегиба: если слева и справа от критической точки
Примерная схема построения графика функции
С учетом всего вышеописанного для исследования функции и дальнейшего построения графика следует придерживаться следующей схеме: 1. Область существования функции. 2. Симметрия графика функции (четность, нечетность). 3. Точки пересечения графика функции с осями координат. 4. Использование первой производной: интервалы возрастания и убывания, экстремумы функции. 5. Использование второй производной: участки выпуклости и вогнутости графика, точки перегиба. 6. Составление сводной таблицы результатов исследования. 7. Построение графика. Пример. Исследовать функцию и построить ее график
Решение. 1. Найдем область определения функции. Дробь определена, если знаменатель отличен от нуля, т. е.
И так, 2. Исследуем функцию на четность. Так как точка 3. Найдём точки пересечения графика функции с осями координат − с осью
и осью График функции пересекается с координатными осями в начале координат − точке 4. Определим экстремумы и интервалы монотонности функции. Для этого найдём первую производную
Функция возрастает при Поскольку при переходе через точку
а при переходе через точку
Итак, 5. Найдем интервалы выпуклости и вогнутости графика функции и точки перегиба. Для этого найдём вторую производную
Левая часть данного уравнения в нуль никогда не обращается Исследуем знак
График функции выпуклый вверх при 6. Составим сводную таблицу.
7. Постоим график.
Неопределенный интеграл
Ранее мы рассматривали способы нахождения производных функции, а также их применение к исследованию функций, что составляет основную задачу раздела высшей математики, называемого дифференциальным исчислением. Далее перейдем к рассмотрению основ интегрального исчисления, которое решает обратную задачу, а именно задачу нахождения функции по ее производной или дифференциалу.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 466; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.44.115 (0.007 с.) |

 называют выпуклым в точке
называют выпуклым в точке  с абсциссой
с абсциссой  , если в некоторой
, если в некоторой  -окрестности точки
-окрестности точки  с абсциссой
с абсциссой 


 с абсциссой
с абсциссой 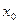 (при условии, что при
(при условии, что при  , то график функции в этой точке выпуклый; если
, то график функции в этой точке выпуклый; если  , то график функции в этой точке вогнутый.
, то график функции в этой точке вогнутый. и
и  (где
(где  - некоторое положительное число), в каждом из которых
- некоторое положительное число), в каждом из которых  сохраняет постоянный знак, то точка
сохраняет постоянный знак, то точка 
 ;
;  .
. .
. не входит в область определения функции, а точка
не входит в область определения функции, а точка  принадлежит области определения функции, т. е. область определения рассматриваемой функции не симметрична относительно начала координат, то функция не является чётной и не является нечётной.
принадлежит области определения функции, т. е. область определения рассматриваемой функции не симметрична относительно начала координат, то функция не является чётной и не является нечётной. :
: ;
;  ;
;  .
.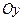 :
:  .
. и решим уравнение
и решим уравнение  ;
;




 ;
;
 ;
;
 ;
;
 .
. и убывает при
и убывает при  .
. первая производная
первая производная 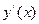 меняет знак с «-» на «+», то это точка минимума:
меняет знак с «-» на «+», то это точка минимума: .,
., первая производная
первая производная 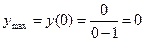
 − точка локального минимума,
− точка локального минимума,  и решим уравнение
и решим уравнение  :
:

 точек перегиба нет.
точек перегиба нет. :
:
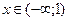
 ;
;
 .
.















 4
4




