
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь производной с наличием экстремумов функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Точка
Определение. Точка
Определение. Точками экстремумов функции называют точки, в которых функция принимает минимальные или максимальные значения.
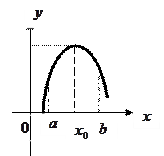
Рис.4 Рис.5
Если точек максимумов или минимумов несколько, то такие максимумы или минимумы называют локальными. Существует тесная связь между наличием экстремумов у дифференцируемых функций и поведением их производных в соответствующих точках и их окрестностях. Теорема. Производная дифференцируемой функции в точке экстремума равна нулю. Эту теорему называют теоремой о необходимом условии существования экстремума дифференцируемой функции в точке, поскольку в ней указывается, что если дифференцируемая функция имеет в некоторой точке экстремум, то в этой точке производная функции обязательно равна нулю. Из рассмотренной теоремы вытекает, что дифференцируемая функция может иметь экстремумы лишь в тех точках, где ее производная равна нулю, т. е. в так называемых стационарных точках функции, являющихся корнями уравнения:
Теорема. Если производная функции 1) этот экстремум является максимумом, если при переходе через точку 2) этот экстремум является минимумом, если при переходе через точку Эту теорему называют теоремой о достаточных условиях существования экстремума дифференцируемой функции в точке, поскольку в ней указаны те условия, которым должна удовлетворять производная, чтобы функция в рассматриваемой точке имела экстремум определенного типа. Справедливо следующее утверждение: точками экстремумов являются лишь те из критических точек функции, при переходе через которые знак производной изменяется на противоположный; при этом изменение знака с плюса на минус свидетельствует о наличии точки максимума, а с минуса на плюс – точки минимума.
|
|||||
|
Последнее изменение этой страницы: 2016-12-15; просмотров: 824; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.89.126 (0.011 с.) |

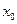 (рис.4) называется точкой максимума функции
(рис.4) называется точкой максимума функции 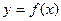 , если существует такая окрестность этой точки, что для всех значений
, если существует такая окрестность этой точки, что для всех значений  , принадлежащих этой окрестности, выполняется неравенство:
, принадлежащих этой окрестности, выполняется неравенство: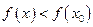 .
.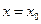 выполняется неравенство:
выполняется неравенство: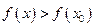 .
.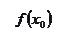
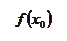

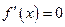 .
.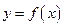 в некоторой точке
в некоторой точке 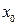 обращается в нуль и при переходе через эту точку изменяет свой знак на противоположный, то данная точка является точкой экстремума функции, причем:
обращается в нуль и при переходе через эту точку изменяет свой знак на противоположный, то данная точка является точкой экстремума функции, причем:


