
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные и дифференциалы высших порядковСодержание книги Поиск на нашем сайте
Пусть функция
Если найти производную функции
т.е. Этот процесс можно продолжить и далее, находя производные степени
Правила нахождения производных высших порядков
Если функции 1) 2) 3)
Это выражение называется формулой Лейбница. Также по формуле Исследование функции с использованием производной Исследование функции на возрастание и убывание
Теорема. 1) Если функция 2) Если функция Доказательство. 1) Если функция
2) Пусть По условию Теорема доказана. Аналогично можно доказать, что если функция Конечно, данное утверждение справедливо, если функция Определение. Функция Оределение. Точки максимума и минимума функции называются точками экстремума. Теорема. (необходимое условие существования экстремума) Если функция Доказательство. Предположим, что функция
Тогда
По определению:
т.е. если А это возможно только в том случае, если при Следствие. Обратное утверждение неверно. Если производная функции в некоторой точке равна нулю, то отсюда вообще говоря не следует, что в этой точке функция имеет экстремум. Например, функция Определение. Критическими точками функции называются точки, в которых производная функции не существует или равна нулю. Рассмотренная выше теорема дает нам необходимые условия существования экстремума, но не достаточные. Например, Вообще говоря, функция Теорема. (Достаточные условия существования экстремума) Пусть функция Если при переходе через точку Доказательство. Пусть Тогда: 1) Если
2) Если
Так как ответы совпадают, то На основе вышесказанного можно сформулировать алгоритм для нахождении наибольшего и наименьшего значения функции на отрезке: 1) Найти критические точки функции. 2) Найти значения функции в критических точках. 3) Найти значения функции на концах отрезка. 4) Выбрать среди полученных значений наибольшее и наименьшее.
Исследование функции на экстремум с помощью Производных высших порядков Пусть в точке Теорема. Если Доказательство. Пусть Так как Для случая минимума функции теорема доказывается аналогично. Если
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 217; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.130.151 (0.006 с.) |

 дифференцируема на некотором интервале. Дифференцируя, находим её первую производную:
дифференцируема на некотором интервале. Дифференцируя, находим её первую производную: .
. , получим вторую производную функции
, получим вторую производную функции  ,
, или
или  .
. .
. .
. и
и  дифференцируемы, то
дифференцируемы, то ;
; ;
;
 .
. может быть найден дифференциал
может быть найден дифференциал  и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е.
и возрастает на этом отрезке, то ее производная на этом отрезке неотрицательна, т.е.  .
. , причем
, причем  для
для  , то эта функция возрастает на отрезке
, то эта функция возрастает на отрезке  при
при  и
и  при
при  . Тогда:
. Тогда:
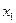 и
и  , принадлежащих отрезку
, принадлежащих отрезку  . Тогда по теореме Лагранжа находим
. Тогда по теореме Лагранжа находим  ,
,  .
. , следовательно,
, следовательно,  , т.е. функция
, т.е. функция 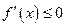 на этом отрезке. Если
на этом отрезке. Если  в промежутке
в промежутке  при любом
при любом  (
(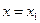 и точка
и точка  , т.е.
, т.е.  .
.
 .
. ,
, , но
, но  , а если
, а если 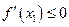 .
.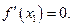 Теорема доказана.
Теорема доказана. имеет производную в точке
имеет производную в точке  равную нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум.
равную нулю, однако в этой точке функция имеет только перегиб, а не максимум или минимум. и
и 
 .
. По теореме Лагранжа:
По теореме Лагранжа:  , где
, где  .
. , то
, то 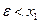 ;
;  . Следовательно
. Следовательно или
или  .
.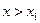 , то
, то  ;
;  ;
; 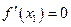 и
и  существует и непрерывна в некоторой окрестности точки
существует и непрерывна в некоторой окрестности точки  и минимум, если
и минимум, если  .
. , то
, то  , то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.
, то характер критической точки неизвестен. Для его определения требуется дальнейшее исследование.


