
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограниченные и неограниченные последовательностиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Последовательность
т.е. все члены последовательности принадлежат отрезку Определение. Последовательность
Определение. Последовательность
Пример. Определение. Число
Обозначение: Пример. Доказать, что предел последовательности Пусть при Пример. Показать, что при Теорема. Последовательность не может иметь более одного предела.
Доказательство. Предположим, что последовательность
Тогда по определению существует такое число
Запишем выражение: Так как Теорема. Если Доказательство. Из
Теорема. Если Необходимо отметить, что обратное утверждение неверно, т.е. из ограниченности последовательности не следует ее сходимость. Например, последовательность
Монотонные последовательности
Определении 1) Если 2) Если 3) Если 4) Если Все эти последовательности называются монотонными. Возрастающие и убывающие последовательности называются строго монотонными. Пример. Пример. Доказать, что последовательность Найдем Найдем знак разности:
Таким образом, Пример. Выяснить является возрастающей или убывающей последовательность
Найдём Заметим, что монотонные последовательности являютс ограниченными по крайней мере с одной стороны. Теорема. Монотонная ограниченная последовательность имеет конечный предел. Доказательство. Рассмотрим монотонную неубывающую последовательность
Эта последовательность ограничена сверху: Так как
Для остальных монотонных последовательностей доказательство аналогично. Теорема доказана. Число е
Рассмотрим последовательность
или
Покажем, что последовательность
Докажем теперь, что при любом n ее члены не превосходят трех:
Таким образом, последовательность
Число
Число
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 1432; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.46.202 (0.006 с.) |

 называется ограниченной, если существует такое число
называется ограниченной, если существует такое число  , что для любого
, что для любого  справедливо неравенство:
справедливо неравенство:
 .
. , что
, что .
.
 – ограничена снизу {1, 2, 3, … }.
– ограничена снизу {1, 2, 3, … }. называется пределом последовательности
называется пределом последовательности  существует такой номер
существует такой номер  , что для всех
, что для всех  выполняется неравенство:
выполняется неравенство:
 . В этом случае говорят, что последовательность
. В этом случае говорят, что последовательность  .
. .
. , т.е.
, т.е.  . Это верно при
. Это верно при 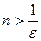 , таким образом, если за
, таким образом, если за  , то утверждение, приведенное выше, выполняется.
, то утверждение, приведенное выше, выполняется. имеет пределом число 2. Имеем
имеет пределом число 2. Имеем  ;
; 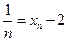 .Для любого положительного числа
.Для любого положительного числа  существует такое натуральное число
существует такое натуральное число  , т.е.
, т.е.  .
. , не равные друг другу.
, не равные друг другу.

 .
. и
и  .
. .
. - любоеположительноечисло, то
- любоеположительноечисло, то  , т.е.
, т.е.  . Теорема доказана.
. Теорема доказана. , то
, то  .
. . В то же время:
. В то же время: , т.е.
, т.е.  , т.е.
, т.е.  не имеет предел. В то же время
не имеет предел. В то же время 
 для всех
для всех  для всех
для всех  для всех
для всех  для всех
для всех  – убывающая и ограниченная;
– убывающая и ограниченная;  – возрастающая и неограниченная.
– возрастающая и неограниченная. монотонная и возрастающая.
монотонная и возрастающая.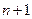 -й член последовательности
-й член последовательности 

 , т.к.
, т.к.  , то знаменатель положительный при любом
, то знаменатель положительный при любом  .
. . Определим разность
. Определим разность 
 , так как
, так как  , т.е.
, т.е. 
 , где
, где  , где
, где 
 ,
, . Отсюда
. Отсюда  или
или  или
или  , т.е.
, т.е.  .Если последовательность
.Если последовательность 

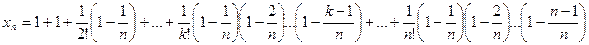
 и сравним его с выражением
и сравним его с выражением  :
: Каждое слагаемое в выражении
Каждое слагаемое в выражении 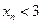 .
.
 - монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е.
- монотонно возрастающая и ограниченная сверху, т.е. имеет конечный предел. Этот предел принято обозначать буквой е. .
. является трпансцендентным числом и приблизительно равно
является трпансцендентным числом и приблизительно равно




