
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ограниченные и неограниченные последователь-Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ности Определение. Последовательность Очевидно, любая ограниченная сверху последователь-ность имеет бесконечное число верхних граней: любое число M*, большее M, также является верхней гранью. Аналогичное замечание имеет место для нижней грани. Определение. Последовательность Если последовательность
где Верно и обратное: если все члены последовательности xn удовлетворяют неравенству (*), то последовательность Последовательность
Примеры: Рассмотрим последовательность 1) Эта последовательность ограничена. Действительно, любое число
2) Последовательность ограничена сверху
3) Последовательность не ограничена. Бесконечно малые и бесконечно большие последо- вательности Определение. Последовательность
Замечание. Любая бесконечно большая последовательность является неограниченной; однако неограниченная последовательность может и не быть бесконечно большой. Пример: последовательность 1, 2, 1, 3, …, 1, n,... является неограниченной, но не является бесконечно большой, т.к. при A>1 неравенство
Определение. Последовательность
Примеры: 1) Доказать, что последовательность а) Пусть
б) Пусть Теперь
2) Докажем, что Теорема. Если
Доказательство: Т.к. для любого Из этой теоремы следует, что члены сходящейся последовательности
где
Теоремы о бесконечно малых последовательно- стях Теорема 1. Сумма двух бесконечно малых последовательностей есть бесконечно малая последовательность. Доказательство. Пусть
Теорема 2. Разность двух бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема доказывается аналогично предыдущей, только вместо неравенства Следствие. Алгебраическая сумма любого конечного числа бесконечно малых последовательностей есть бесконечно малая последовательность.
Теорема 3. Бесконечно малая последовательность ограничена.
Доказательство: Пусть
Теорема 4. Произведение ограниченной последовательности на бесконечно малую последовательность представляет собой бесконечно малую последовательность. Доказательство: Пусть
Следствие. Произведение любого конечного числа бесконечно малых последовательностей представляет собой бесконечно малую последовательность.
Теорема 5. Если Доказательство: Во-первых, надо четко понимать, почему в формулировке теоремы имеются слова “начиная с некоторого номера”. Дело в том, что у бесконечно большой последовательности могут встретиться нулевые члены и тогда последовательность Докажем теперь, что Таким образом, доказано, что Доказательство второй части теоремы провести самостоятельно (оно аналогично только что приведенному). Основные теоремы о пределах
Теорема 1. Сходящаяся последовательность имеет только один предел.
Доказательство:
Предположим, что сходящаяся последовательность
Теорема 2. Сходящаяся последовательность ограничена.
Доказательство: Пусть
Еще несколько теорем о пределах. Пусть даны две сходящихся последовательности
Значения
Эти формулы фактически задают арифметические действия с переменными, имеющими предел.
Доказательство равенства (1): Пусть Доказательство равенства (2): Представим Для доказательства равенства (3) сначала докажем лемму. Лемма. Если последовательность
Доказательство: Пусть
Доказательство равенства (3): Если
Таким образом
Итак, мы выяснили, что арифметические операции над сходящимися последовательностями приводят к таким же операциям над их пределами. Этот очень важный вывод поможет вычислять пределы различных последовательностей. Оказывается, что если элементы (члены) сходящихся последовательностей удовлетворяют некоторым неравенствам, то таким же неравенствам удовлетворяют и пределы их последовательностей.
Теорема. Если элементы сходящейся последовательности
Доказательство: Пусть начиная с некоторого номера все элементы
Следствие 1. Если элементы
Следствие 2. Если все элементы сходящейся последовательности
Теорема. Пусть Доказательство: Пусть N* – номер, начиная с которого выполняются неравенства Очевидно, что при Т.к. Пусть
|
|||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3982; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.98.91 (0.008 с.) |

 называется ограниченной сверху (снизу), если существует такое число M (m), что каждый член xn последовательности удовлетворяет неравенству
называется ограниченной сверху (снизу), если существует такое число M (m), что каждый член xn последовательности удовлетворяет неравенству  При этом M и m называются соответственно верхней и нижней гранями последовательности
При этом M и m называются соответственно верхней и нижней гранями последовательности 
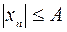 , (*)
, (*)
 .
.
 .
. является ее верхней гранью, а любое число
является ее верхней гранью, а любое число  – нижней гранью.
– нижней гранью. –1, –4, –9,..., –n2,....
–1, –4, –9,..., –n2,.... и не ограничена снизу.
и не ограничена снизу. –1, 2, –3, 4,....
–1, 2, –3, 4,.... такой, что при
такой, что при  все члены xn этой последовательности удовлетворяют неравенству
все члены xn этой последовательности удовлетворяют неравенству  называется бесконечно малой, если для любого
называется бесконечно малой, если для любого  можно указать номер
можно указать номер  такой, что при
такой, что при  этой последовательности удовлетворяют неравенству
этой последовательности удовлетворяют неравенству  .
. является бесконечно большой, а при
является бесконечно большой, а при  бесконечно малой.
бесконечно малой. . Тогда
. Тогда  , где
, где  .
. +(положительные члены), т.е.
+(положительные члены), т.е.  Теперь зафиксируем произвольное число A>0 и выберем N столь большим, чтобы
Теперь зафиксируем произвольное число A>0 и выберем N столь большим, чтобы  (например, выберем
(например, выберем  ). Тогда
). Тогда  . Но при
. Но при  и
и 
 ,т.е.
,т.е. 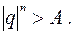 Утверждение доказано.
Утверждение доказано. . В этом случае
. В этом случае 
 . Зафиксируем произвольное
. Зафиксируем произвольное 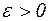 и выберем номер N из условия
и выберем номер N из условия  . Т.к.
. Т.к.  и при
и при  , то из полученных неравенств вытекает, что
, то из полученных неравенств вытекает, что  . Утверждение доказано.
. Утверждение доказано. – бесконечно малая последовательность. В самом деле, если
– бесконечно малая последовательность. В самом деле, если  Поэтому по заданному
Поэтому по заданному  достаточно выбрать номер N из условия
достаточно выбрать номер N из условия  . Тогда при
. Тогда при  и утверждение доказано.
и утверждение доказано. то
то  – бесконечно малая последовательность.
– бесконечно малая последовательность. такой, что при
такой, что при  , это и означает, что при
, это и означает, что при  , т.е.
, т.е.  – бесконечно малая последовательность.
– бесконечно малая последовательность.
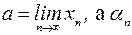 – бесконечно малая последователь-ность.
– бесконечно малая последователь-ность. и
и  – бесконечно малые последовательности. Докажем, что
– бесконечно малые последовательности. Докажем, что  – бесконечно малая последовательность. Пусть
– бесконечно малая последовательность. Пусть  , а N2 – номер, начиная с которого
, а N2 – номер, начиная с которого  . Тогда, если
. Тогда, если  , то при
, то при  , т.е.
, т.е.  . Теорема доказана.
. Теорема доказана. следует взять неравенство
следует взять неравенство  .
.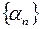 – бесконечно малая последовательность и
– бесконечно малая последовательность и  . Тогда любой член последовательности с номером
. Тогда любой член последовательности с номером 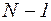 членов выберем наибольший по модулю:
членов выберем наибольший по модулю:  и зададим
и зададим  . Тогда для всех членов последовательности
. Тогда для всех членов последовательности  , что и означает ограниченность последовательности. Теорема доказана.
, что и означает ограниченность последовательности. Теорема доказана. Возьмем произвольное
Возьмем произвольное  можно указать номер N такой, что при
можно указать номер N такой, что при  . Тогда при
. Тогда при 
 . Поэтому последовательность
. Поэтому последовательность  – бесконечно малая. Теорема доказана.
– бесконечно малая. Теорема доказана. , которая является бесконечно малой последовательностью. Если все элементы бесконечно малой последовательности
, которая является бесконечно малой последовательностью. Если все элементы бесконечно малой последовательности  не равны нулю, то последовательность
не равны нулю, то последовательность  бесконечно большая.
бесконечно большая. оказывается определенной и формулировка теоремы справедлива для n>N*.
оказывается определенной и формулировка теоремы справедлива для n>N*. можно указать номер
можно указать номер  такой, что при
такой, что при  . Поэтому, начиная с указанного номера N, выполняется неравенство
. Поэтому, начиная с указанного номера N, выполняется неравенство  .
.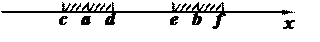
 . Тогда
. Тогда  можно представить в виде
можно представить в виде  , где
, где  . Это неравенство выполняется для всех n, а это означает ограниченность последовательности
. Это неравенство выполняется для всех n, а это означает ограниченность последовательности  .
. определяют последовательности
определяют последовательности  . Справедливы равенства:
. Справедливы равенства: ; (1)
; (1) ; (2)
; (2) , если
, если 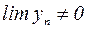 . (3)
. (3) Выберем
Выберем  Тогда при
Тогда при 
 Равенство доказано.
Равенство доказано. и
и 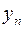 в виде:
в виде:  где
где 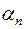 и
и  – члены бесконечно малых последовательностей. Тогда
– члены бесконечно малых последовательностей. Тогда  Поэтому
Поэтому  . При этом последовательность
. При этом последовательность  – бесконечно малая последовательность, т.к. бесконечно малой последовательностью является каждая из трех переменных
– бесконечно малая последовательность, т.к. бесконечно малой последовательностью является каждая из трех переменных 

 . Поэтому последовательность
. Поэтому последовательность  также бесконечно малая, а последовательность
также бесконечно малая, а последовательность 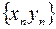 сходится и ab – ее предел. Равенство доказано.
сходится и ab – ее предел. Равенство доказано. сходится и имеет отличный от нуля предел b, то, начиная с некоторого номера, определена последовательность
сходится и имеет отличный от нуля предел b, то, начиная с некоторого номера, определена последовательность  , которая является ограниченной.
, которая является ограниченной. начиная с которого выполняется неравенство
начиная с которого выполняется неравенство  или
или  Тогда
Тогда 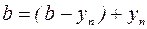 ,
, 
 , т.е.
, т.е.  . Поэтому при
. Поэтому при  . Следовательно, начиная с этого N мы можем рассматривать последовательность
. Следовательно, начиная с этого N мы можем рассматривать последовательность  , где
, где  – бесконечно малые последовательности. Тогда
– бесконечно малые последовательности. Тогда
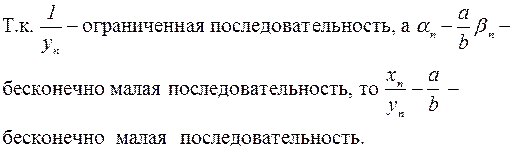
 Равенство (3) доказано.
Равенство (3) доказано. , то и предел a этой последовательности удовлетворяет неравенству
, то и предел a этой последовательности удовлетворяет неравенству  .
. Требуется доказать, что
Требуется доказать, что  . Предположим противное, т.е. что
. Предположим противное, т.е. что  . Введем
. Введем  . Для этого
. Для этого  или
или  . Из правого неравенства тогда следует, что
. Из правого неравенства тогда следует, что  , а это противоречит условию теоремы. Случай
, а это противоречит условию теоремы. Случай  рассматривается аналогично. Теорема доказана.
рассматривается аналогично. Теорема доказана. сходящихся последовательностей, начиная с некоторого номера, удовлетворяют неравенству
сходящихся последовательностей, начиная с некоторого номера, удовлетворяют неравенству  , то и их пределы удовлетворяют такому же неравенству
, то и их пределы удовлетворяют такому же неравенству  .
. , то и ее предел С также находится на этом отрезке.
, то и ее предел С также находится на этом отрезке. и
и  – сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности
– сходящиеся последовательности, имеющие общий предел a. Пусть, кроме того, начиная с некоторого номера, элементы последовательности 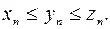 Тогда последовательность
Тогда последовательность 
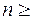 N*
N* 
 то для любого
то для любого  .
. Очевидно, при
Очевидно, при  , т.е. последовательность
, т.е. последовательность  – бесконечно малая последовательность. Теорема доказана.
– бесконечно малая последовательность. Теорема доказана.


