
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полное приращение и полный дифференциал. Использование дифференциала для приближенных вычислений
Мы уже знаем, что полное приращение функции двух переменных z=f(x,y) записывается в виде:
Dz = f(х+Dх, у+Dу) – f(x,y).
Пусть в точке (х,у) существуют и непрерывны обе частные производные
Dz = [f(x+Dx, y+Dy) – f(x, y+Dy)] + [f(x, y+Dy) – f(x,y)].
Применим теорему Лагранжа:
Заметим, что в силу непрерывности частных производных
Но это означает, что
где g1®0 и g2®0, если Dх®0 и Dу®0 (или если
Тогда полное приращение Dz можно записать в виде
Первые два члена в этой формуле – основные, а слагаемые g1×Dх и g2×Dу – бесконечные малые более высокого порядка, чем первые два члена. Другими словами, можно дать следующее определение. Определение. Функция z = f(x, y), полное приращение которой в данной точке (х,у) может быть представлено в виде (3.6.1), называется дифференцируемой в данной точке; линейная часть приращения называется полным дифференциалом:
dz=f 'x(x,y)Dx+f 'y(x,y)Dy.
Обычно обозначают Dх = dx, Dу = dy, а формула для полного дифференциала имеет вид
С точностью до бесконечно малых высшего порядка относительно Dr можно записать приближенное равенство:
Dz» dz, (3.6.3)
которое используется для приближенных вычислений. Примеры. 1. z=xy. Найти полный дифференциал и полное приращение в точке (2;3) при Dх=0,1, Dу=0,2. Dz = (х + Dх)(у + Dу) – ху = уDх + хDу + DхDу;
Dz=0,72; dz=0,7.
2. Задача. Вычислить объем материала, нужно для изготовления цилиндрического стакана следующих размеров: - радиус внутреннего цилиндра R; - высота внутреннего цилиндра H; - толщина стенок и дна стакана l.
Точное решение: V=p(R+l)2(H+l)–pR2H=p(2RHl+R2l+Hl2+2Rl2+l3). (*)
Приближенное решение: f = pR2H – объем внутреннего цилиндра. Это функция двух переменных R и Н. Если увеличить R и Н на l, то функция f получит приращение Df. Тогда V=Df. Приближенно:
V» p(2RHl + R2l). (**)
Сравнивая (*) и (**), замечаем, что эти выражения отличаются на величину p(Hl2+2Rl2+l3), состоящую из членов второго и третьего порядка малости относительно l (естественно, мы должны считать l<<R, l<<H). Числовой пример: R=4 см, Н=20 см, l=0,1 см. V=17,881 p –точное значение, V»17,6 p – приближенное значение. Ошибка
Сложная функция и ее полная производная
Пусть z=F(u,v), (3.7.1)
а u и v являются функциями независимых переменных х и у.
u=j(x,y), v=y(x,y). (3.7.2)
В этом случае z есть сложная функция х и у. Будем рассматривать вопрос о частных производных
Здесь g1 и g2 – бесконечно малые при Dх®0. Разделим последнее равенство на Dх и перейдем к пределу при Dх®0:
Аналогично
(3.7.3) и (3.7.4) – формулы для частных производных сложной функции. Пример. z=ln(u2+v),
Тогда
Для случая большего числа переменных формулы (3.7.3) и (3.7.4) естественным образом обобщаются. Рассмотрим следующий случай: дана функция z=F(x,y,u,v), где y,u,v зависят только от одной переменной х: y=f(x), u=j(x), v=y(x).
В этом случае, по сути дела, z является функцией только одной переменной х и можно ставить вопрос о нахождении производной Очевидно
Но
Эта формула носит название формулы полной производной
Пример.
Производная неявно заданной функции
Если неявная функция одной переменной задана уравнением
то производная
Формула (3.8.2) носит название производной неявно заданной функции одной переменной. По аналогии неявная функция двух переменных (
Если теперь искать, например частную производную
Аналогично
Разумеется, в формулах (3.8.3) и (3.8.4) следует считать
Пример. Неявная функция трех переменных задана соотношением
Пусть
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 422; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.33.41 (0.018 с.) |
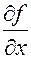 и
и  . Перепишем Dz в виде
. Перепишем Dz в виде
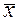 Î(х, х+Dх);
Î(х, х+Dх);
 Î(у, у+Dу);
Î(у, у+Dу);

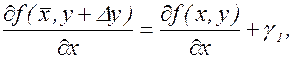

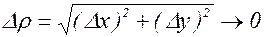 ).
).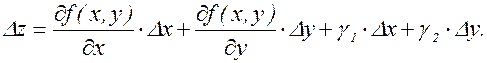 (3.6.1)
(3.6.1)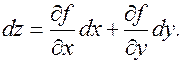 (3.6.2)
(3.6.2)
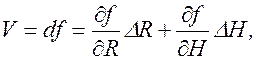
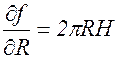 ,
, 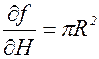 ,
, 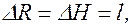
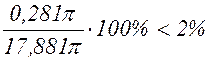 .
.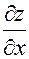 и
и  . Дадим приращение Dх, не меняя у. Тогда u и v получат приращения Dхu и Dхv:
. Дадим приращение Dх, не меняя у. Тогда u и v получат приращения Dхu и Dхv:
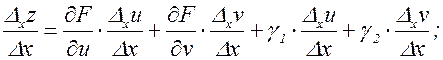
 (3.7.3)
(3.7.3)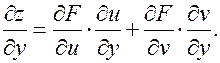 (3.7.4)
(3.7.4)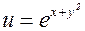 ; v=x2+y. Найти
; v=x2+y. Найти 
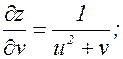
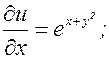
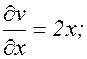
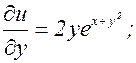
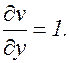


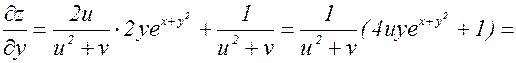

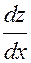 (в отличие от
(в отличие от 
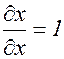 , а производные
, а производные  и
и 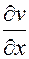 являются по существу не частными, а полными производными, т.к. у, u и v зависят только от х:
являются по существу не частными, а полными производными, т.к. у, u и v зависят только от х: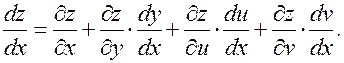 (3.7.5)
(3.7.5)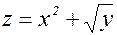 ; у=sin x. Найти
; у=sin x. Найти 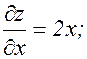


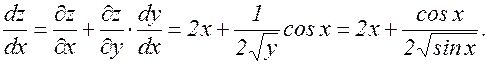
 , (3.8.1)
, (3.8.1)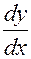 находится по известной формуле:
находится по известной формуле: . (3.8.2)
. (3.8.2)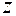 есть функция
есть функция 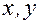 ) задается уравнением
) задается уравнением .
. считается постоянной и можно действовать по формуле (3.8.2). Тогда
считается постоянной и можно действовать по формуле (3.8.2). Тогда
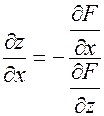 . (3.8.3)
. (3.8.3)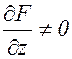 . Эти формулы обобщаются на любое число переменных.
. Эти формулы обобщаются на любое число переменных.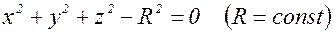 . Найти
. Найти  . Тогда
. Тогда .
.


