
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частные производные высших порядковСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть дана функция двух переменных z=f(x,y). Ее частные производные
Эти производные обозначаются так:
Можно продолжать этот процесс, дифференцируя вторые производные по х или у и получая третьи производные и т.д.
Аналогично определяются производные любого порядка от функции любого числа переменных.
Пример. Вычислить производные 2-го порядка функции f(x,y)=х2у+у3.
В данном примере оказалось, что Теорема (без доказательства). Если функция f(x,y) и ее частные производные до второго порядка включительно определены и непрерывны в окрестности точки (х,у), то в этой окрестности
Из этой теоремы следует, что смешанные частные производные второго порядка не зависят от порядка дифференцирования. Это свойство дифференцируемых функций следует иметь в виду при выполнении практических расчетов.
Производная по направлению Пусть в пространственной области
Этот вектор является диагональю параллелепипеда со сторонами
Будем считать, что функция
где
Очевидно, Пусть теперь
Из этой формулы следует, что производная функции по любому направлению может быть вычислена, если известны все ее частные производные. Сами же частные производные являются производными по некоторым направлениям. Например, если выбрать в качестве заданного направления положительное направление оси то
Аналогично производные
Пример. а) Найти производную функции б) Найти производную функции в) Найти производную функции
Решение. а) Прежде, чем привести решение этой задачи, заметим, что формула (3.10.3) пригодна и для функций двух переменных. Для этого достаточно положить Итак, в нашем случае
Тогда
б) Сначала найдем направляющие косинусы вектора
Теперь вычислим частные производные:
В точке
в) Воспользуемся тем, что
Отсюда, т.к. углы
Окончательно получаем
Градиент Пусть в некоторой области
Этот вектор называется градиентом функции
Теорема. Пусть дано скалярное поле
Тогда производная по направлению вектора
Геометрически формулу (3.11.1) можно трактовать с помощью следующего рисунка
Здесь
Из определения градиента и формул (3.11.1) (3.11.2) следуют свойства градиента: 1) Производная в данной точке по направлению 2) Производная по направлению, перпендикулярном градиенту, равна нулю: в этом случае Пример 1. Найти градиент функции
Для функции двух переменных
В нашем случае
Тогда
Пример 2. Для функции
поэтому Очевидно,
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 593; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.111 (0.007 с.) |

 и
и  , вообще говоря, являются функциями двух переменных х и у. Поэтому эти функции можно снова дифференцировать по х и у. Таких частных производных второго порядка всего четыре, т.к. каждую из производных
, вообще говоря, являются функциями двух переменных х и у. Поэтому эти функции можно снова дифференцировать по х и у. Таких частных производных второго порядка всего четыре, т.к. каждую из производных 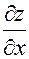 и
и  можно дифференцировать как по х, так и по у.
можно дифференцировать как по х, так и по у. – дифференцируем два раза подряд по х;
– дифференцируем два раза подряд по х; – сначала дифференцируем по х, затем по у;
– сначала дифференцируем по х, затем по у; – сначала дифференцируем по у, затем по х;
– сначала дифференцируем по у, затем по х;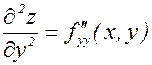 – два раза дифференцируем по у.
– два раза дифференцируем по у. – частная производная n -го порядка, дифференцирование ведется сначала р раз по х, затем n–p раз по у.
– частная производная n -го порядка, дифференцирование ведется сначала р раз по х, затем n–p раз по у.

 , т.е. смешанная производная по х и у оказалась не зависящей от порядка дифференцирования. Оказывается, что это совсем не случайно.
, т.е. смешанная производная по х и у оказалась не зависящей от порядка дифференцирования. Оказывается, что это совсем не случайно. .
. задана функция трех переменных
задана функция трех переменных 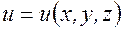 . Выберем в этой области две точки:
. Выберем в этой области две точки:  и
и 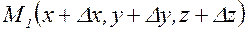 (знаки приращений
(знаки приращений 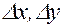 и
и 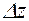 могут быть произвольными) и проведем вектор
могут быть произвольными) и проведем вектор  (см. рис.).
(см. рис.).
 . Очевидно, его длина равна
. Очевидно, его длина равна .
.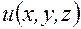 дифференцируема и запишем полное приращение
дифференцируема и запишем полное приращение  при переходе от точки
при переходе от точки  к точке
к точке 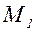 в виде
в виде , (3.10.1)
, (3.10.1) и
и  стремятся к нулю, если
стремятся к нулю, если  . Разделим все члены в (3.10.1) на
. Разделим все члены в (3.10.1) на  :
: .
. . (3.10.2)
. (3.10.2) – направляющие косинусы вектора
– направляющие косинусы вектора  .
.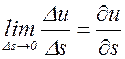 называют производной функции
называют производной функции 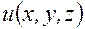 в точке
в точке  по направлению вектора
по направлению вектора  . (3.10.3)
. (3.10.3) ,
, , тогда
, тогда  и
и
 и
и 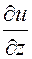 являются производными вдоль положительных направлений координатных осей
являются производными вдоль положительных направлений координатных осей  и
и 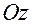 .
. в точке
в точке  в направлении, составляющем с осью
в направлении, составляющем с осью 
 º;
º; в точке
в точке  в направлении вектора
в направлении вектора  ;
; в точке
в точке 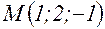 в направлении, составляющим одинаковые острые углы с направлениями координатных осей.
в направлении, составляющим одинаковые острые углы с направлениями координатных осей. , т.е. исключить в этой формуле третье слагаемое.
, т.е. исключить в этой формуле третье слагаемое. º,
º,  º, т.е.
º, т.е.  .
. .
.
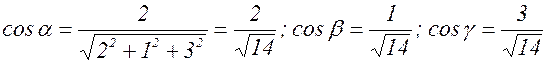 .
. .
.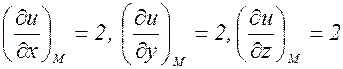 . Итак,
. Итак,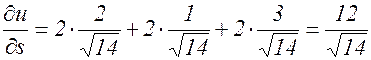 .
.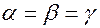 и
и 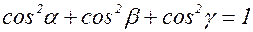 .
. – острые, то
– острые, то  .
.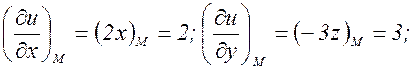
 .
. .
. :
: .
. имеется свой вектор градиента). Сами же значения
имеется свой вектор градиента). Сами же значения  – скаляры, т.е. числа).
– скаляры, т.е. числа). и в этом скалярном поле определено поле градиентов
и в этом скалярном поле определено поле градиентов на вектор
на вектор  пр
пр  . (3.11.1)
. (3.11.1)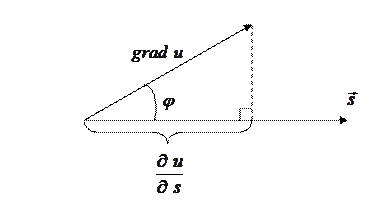
 – угол между векторами
– угол между векторами  . (3.11.2)
. (3.11.2) на приведенном выше рисунке); это наибольшее значение производной равно
на приведенном выше рисунке); это наибольшее значение производной равно  . Другими словами, скалярное поле
. Другими словами, скалярное поле  . Таким образом, в направлении, перпендикулярном градиенту, функция не изменяется (мы находимся на поверхности заданного уровня
. Таким образом, в направлении, перпендикулярном градиенту, функция не изменяется (мы находимся на поверхности заданного уровня 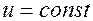 ).
).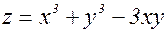 в точке
в точке 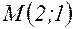 .
.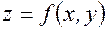 градиент, очевидно, находится в виде:
градиент, очевидно, находится в виде: .
.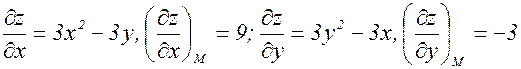 .
. .
. .
.
 ,
, .
. , а направляющие косинусы вектора
, а направляющие косинусы вектора  .
.


