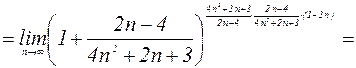Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Свойства функций, непрерывных в точкеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема 1. Если функции Доказательство: Следует из свойств пределов и определения непрерывности. Например:
Теорема 2 (непрерывность сложной функции). Пусть функция
Доказательство. Т.к. функция
Формулу (*) можно записать в виде Можно также записать: Это правило замены переменных, которое очень часто используется при вычислении пределов. В качестве примеров докажем непрерывность некоторых элементарных функций. 1.
Функция
2.
Функция
Справедлива теорема (без доказательства). Любая элементарная функция непрерывна в каждой точке, в которой она определена. Подчеркну, что речь идет не только об основных элементарных функциях, а вообще об элементарных функциях, т.е. таких, которые получены из основных элементарных путем конечного числа арифметических операций и взятия функции от функции.
Теорема об ограниченности непрерывной функции. Если функция
Доказательство. Из определения непрерывности следует, что
Два замечательных предела Для вывода формул первого и второго замечательных пределов сначала докажем вспомогательную теорему (лемму).
Лемма. Пусть в некоторой
Доказательство. Пусть
1. Первый замечательный предел
Функция
Из точки M проведем
Поскольку OM=OA=1, то
Sсектора= OMA =
Тогда неравенство (1) имеет вид:
Т.к. x -острый угол и
Это неравенство получено в предположении, что x>0. Если же x<0, то cos(–x) = cosx и
2. Второй замечательный предел
Мы уже знаем, что В самом деле, любое положительное значение x заключено между двумя положительными и целыми числами:
При этом выполняются неравенства:
Если
Пределы оказались одинаковыми. Поэтому в соответствии с леммой Мы доказали, что если x всегда положителен и Можно доказать, что этот предел равен e при произвольном стремлении x к
Этот же предел можно записать в другой форме, обозначив
Теперь рассмотрим примеры вычисления пределов.
Пример 1. Найти
Пример 2. Найти
Пример 3. Найти Пример 4.
Используем замену переменной Тогда
Пример 5.
Пример 6.
Пример 7.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 495; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.119 (0.006 с.) |

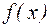 и
и 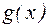 непрерывны в точке
непрерывны в точке  , то функции
, то функции  (с – константа),
(с – константа),  , то и
, то и 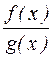 также непрерывны в точке
также непрерывны в точке 
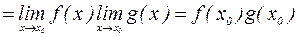 .
. непрерывна в точке
непрерывна в точке 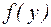 непрерывна в точке
непрерывна в точке 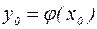 . Тогда сложная функция
. Тогда сложная функция 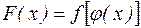 также непрерывна в точке
также непрерывна в точке 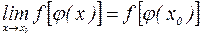 . (*)
. (*)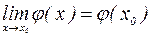
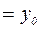 . Т.к функция
. Т.к функция 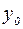 , то
, то 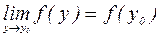 , но т.к. при любом стремлении
, но т.к. при любом стремлении 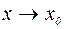 и
и  , то
, то 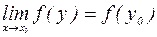 , т.е.
, т.е. 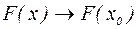 . Сложная функция
. Сложная функция 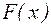 непрерывна.
непрерывна.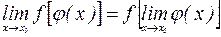 , которая может быть использована при вычислении пределов.
, которая может быть использована при вычислении пределов.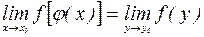 , где
, где 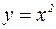 – непрерывна в любой точке
– непрерывна в любой точке 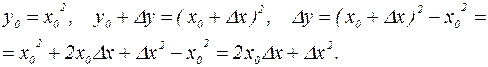
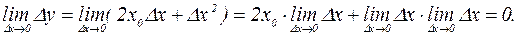
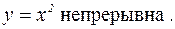
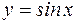 – непрерывна в любой точке
– непрерывна в любой точке 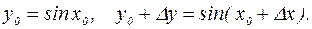
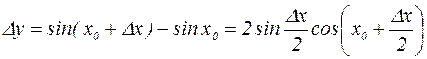 ;
;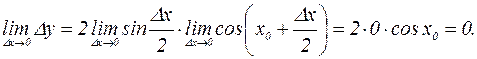
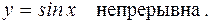
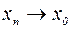 , и при этом
, и при этом  . Сходящаяся же последовательность
. Сходящаяся же последовательность 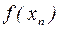 ограничена, поэтому и
ограничена, поэтому и 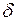 -окрестности точки
-окрестности точки  , причем
, причем 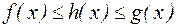 и
и 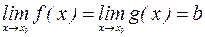 . Тогда
. Тогда  .
. – произвольная последовательность,
– произвольная последовательность,  при
при  , элементы которой лежат в указанной
, элементы которой лежат в указанной 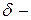 окрестности точки
окрестности точки 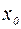 и не равны
и не равны 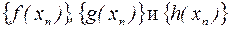 – соответствующие последовательности значений функции. По условию
– соответствующие последовательности значений функции. По условию  и
и  . Но тогда в силу теоремы, доказанной для последовательности,
. Но тогда в силу теоремы, доказанной для последовательности,  . Поскольку
. Поскольку  .
.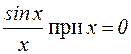 не определена. Найдем ее предел при
не определена. Найдем ее предел при 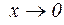 . Для этого рассмотрим на окружности радиуса 1 два радиуса OA и OM, острый угол между которыми равен x (в радианах).
. Для этого рассмотрим на окружности радиуса 1 два радиуса OA и OM, острый угол между которыми равен x (в радианах).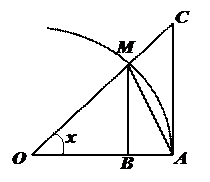
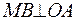 , а продолжив OM, из точки С проведем
, а продолжив OM, из точки С проведем  Из рисунка ясно, что
Из рисунка ясно, что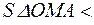 Sсектора OMA <
Sсектора OMA <  . (1)
. (1)

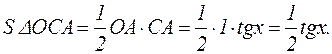
 .
.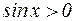 , разделив это неравенство на sinx>0, получим
, разделив это неравенство на sinx>0, получим или
или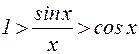 . (2)
. (2)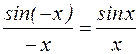 , поэтому оно справедливо и при x <0. Из неравенства (2) следует, что переменная
, поэтому оно справедливо и при x <0. Из неравенства (2) следует, что переменная 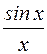 заключена между двумя переменными, имеющими при
заключена между двумя переменными, имеющими при  ;
;  . Поэтому согласно указанной лемме
. Поэтому согласно указанной лемме 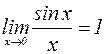 .
.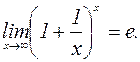
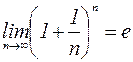 . При этом n принимает целые положительные значения. Оказывается, если
. При этом n принимает целые положительные значения. Оказывается, если  , принимая любые, в том числе и дробные значения, предел также оказывается равным e.
, принимая любые, в том числе и дробные значения, предел также оказывается равным e. .
.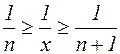 ;
;  ;
;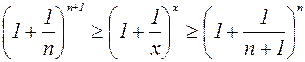 .
.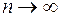 . Найдем пределы, к которым стремятся переменные, между которыми заключена переменная
. Найдем пределы, к которым стремятся переменные, между которыми заключена переменная  .
.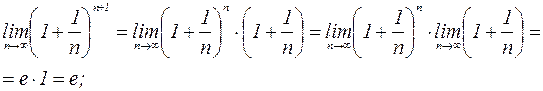
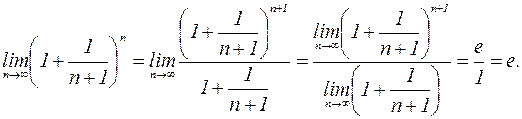
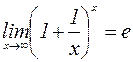 .
.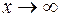 , то
, то  или
или 

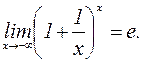
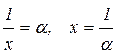 и рассматривая
и рассматривая 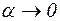 .
.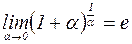 .
.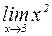 . Т.к. функция
. Т.к. функция 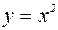 непрерывна в любой точке, то
непрерывна в любой точке, то 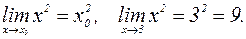
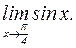
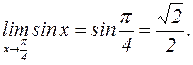
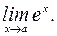 Т.к. функция
Т.к. функция 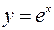 непрерывна в каждой точке (
непрерывна в каждой точке (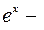 элементарная функция), то
элементарная функция), то 
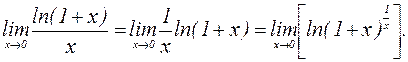
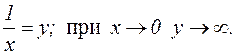
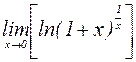 =
= 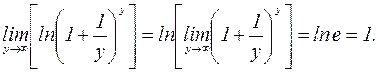
 .
.