
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эквивалентные бесконечно малые функции и ихСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
применение для вычисления пределов Определение. Бесконечно малые функции Пишут так:
Теорема. Пусть в окрестности точки Это равенство понимается в смысле: если существует предел его правой части, то существует равный ему предел левой части (и обратно). Отсюда же следует, что если один из пределов не существует, то не существует и другой. Доказательство. Пусть
Аналогично доказывается обратное утверждение.
Пары эквивалентных бесконечно малых, которые используют при вычислении пределов:
9)
Монотонные функции. Теорема о существовании И непрерывности обратной функции Определение. Функция
Неубывающие и невозрастающие функции называются монотонными. Если неравенства строгие, то функция называется возрастающей (убывающей) на отрезке. Возрастающие и убывающие функции называются строго монотонными. Теорема. Рассмотрим непрерывную строго возрастающую функцию
Доказательство существования. Поскольку каждому значению
Доказательство возрастания. Из условия возрастания Но
Доказательство непрерывности обратной функции. Докажем непрерывность обратной функции
Выберем
Пусть теперь С учетом (*) можно записать, что В силу возрастания функции
Но Разрывы первого и второго рода
Определение.
Рассмотрим график
Другие возможные случаи разрывов.
Если функция f имеет конечные пределы Если
Если доопределить
Пример разрывной функции (функция Кронекера):
Точка
Если у функции не существует ни левого, ни правого предела, либо одного из них, либо эти пределы бесконечны в точке С, то функция имеет разрыв II рода.
Пример 1.
Пример 2.
Эта функция не имеет в точке
Пример 3.
Точки
Функции, непрерывные на отрезке
Определение. Функция Теорема 1. Если функция непрерывна на отрезке Теорема 2 (теорема Вейерштрасса). Если функция
Теорема 3. Если функция
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 2576; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.0.57 (0.012 с.) |

 называются эквивалентными бесконечно малыми при
называются эквивалентными бесконечно малыми при 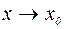 , если
, если 
 при
при 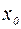 , за исключением, быть может, ее самой, задана функция
, за исключением, быть может, ее самой, задана функция 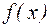 и бесконечно малые функции
и бесконечно малые функции 
 тогда
тогда 

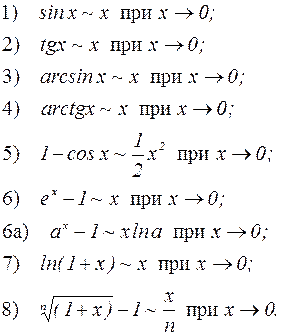
 при
при 
 называется неубывающей (невозрастающей) на отрезке
называется неубывающей (невозрастающей) на отрезке  , если для любых
, если для любых 
 выполняется неравенство
выполняется неравенство  .
. Тогда существует обратная к f функция
Тогда существует обратная к f функция  , однозначная, строго возрастающая и непрерывная на
, однозначная, строго возрастающая и непрерывная на  .
.
 соответствует только одно значение
соответствует только одно значение 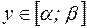 , то любому значению y из
, то любому значению y из  можно поставить в соответствие именно то значение x, для которого
можно поставить в соответствие именно то значение x, для которого  обозначим это соответствие так:
обозначим это соответствие так:  Верно и обратное утверждение: если
Верно и обратное утверждение: если 


 и получаем: если
и получаем: если  т.е. обратная функция – возрастающая.
т.е. обратная функция – возрастающая.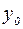 . Обозначим
. Обозначим  и выберем произвольное
и выберем произвольное  , такое, что
, такое, что  . Пусть
. Пусть 

 Тогда, очевидно,
Тогда, очевидно, а
а  . (*)
. (*) , т.е.
, т.е. 
 .
. .
.



 , поэтому
, поэтому  или
или  А это и означает, что функция
А это и означает, что функция 
 . Точка с называется точкой разрыва функции
. Точка с называется точкой разрыва функции  , или если она определена в этой точке, но не является в ней непрерывной.
, или если она определена в этой точке, но не является в ней непрерывной.
 . Стрелка в точке В означает, что точка В в область значений функции
. Стрелка в точке В означает, что точка В в область значений функции  , функция
, функция 
 и
и  , но
, но  , то функция имеет в точке
, то функция имеет в точке  разрыв I рода.
разрыв I рода. , то в точке
, то в точке  устранимая особенность.
устранимая особенность.
 , то получим непрерывную функцию.
, то получим непрерывную функцию.


 является точкой разрыва I рода.
является точкой разрыва I рода.
 ;
;
 –точка разрыва II рода.
–точка разрыва II рода. Ее график имеет вид:
Ее график имеет вид:





 , – точки разрыва II рода. В них
, – точки разрыва II рода. В них  , если она непрерывна во всех точках интервала
, если она непрерывна во всех точках интервала  , непрерывна справа в точке a, слева в точке b.
, непрерывна справа в точке a, слева в точке b. , такое, что
, такое, что  для всех
для всех  .
. , такие, что
, такие, что  для всех
для всех  не равны нулю и имеют противоположные знаки, то на интервале
не равны нулю и имеют противоположные знаки, то на интервале  .
.


