
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило вычисления пределов, отношения многочленов на бесконечности.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Множества. В математике часто приходится рассматривать те или иные группы объектов как единое целое: цифры: 0,1,2,3,4.5,6,7,8,9. натуральные числа: 1, 2, 3, 4,... треугольники и т.д. Все эти различные совокупности называют множествами. Множество — одно из основ- ных математических понятий, поэтому не имеет явного определения, а поясняется на примерах. Возникло это понятие в конце 19 века как обобщение понятий: класс группа, набор и т.п. В быту множеством называют большое количество элементов. В математике рассматривают множества, состоящие и из одного объектами не содержащие ни одного объекта. Обозначают множества заглавными буквами латинского алфавита: А.В.С Z. Множество, не содержащее ни одного элемента, называют пустым и обозначают символом 0 Например, пустым является множество решений уравнения 5: х = 0. Для некоторых числовых множеств приняты стандартные обозначения: N — множество натуральных чисел, Z — множество целых чисел, Q — множество рациональных чисел, R — множество действительных чисел. Объекты, из которых образовано множество, называют его элементами, их принято обозначать строчными буквами латинского алфавита: а, Ь, с,...,. Множества бывают конечные и бесконечные. Например, множество букв русского алфавита — конечное, а множество точек на прямой — бесконечное множество. СПОСОБЫ ЗАДАНИЯ МНОЖЕСТВ Так как понятие множества не имеет явного определения необходимо научиться узнавать является ли данная совокупность множеством или нет. Считают, что множество определяется своими элементами. Множество задано, если о любом объекте можно сказать, принадлежит он этому множеству, либо не принадлежит. Способы задания множеств: — перечисляют все его элементы: А = { 3,4,5,6,7 }, (применяется для задания множеств с небольшим количеством элементов, иногда для бесконечных). — указывают характеристическое свойство элементов: В — множество двузначных чисел, К - множество цветов спектра, (применяется для задания конечных и бесконечных множеств). Характеристическое свойство — это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит. Так, характеристическое свойство элементов множества В — "быть двузначным числом". При обучении дошкольников математике большое место отводится формированию у детей представлений о множестве, его элементах, способах задания и операциях между множествами. В явном виде множества не изучаются, но пронизывают все задания и вопросы. Названные способы задания множеств взаимосвязаны — если конечное множество задано с помощью характеристического свойства, то можно его элементы перечислить, и наоборот.)
ОПЕРАЦИИ НАД МНОЖЕСТВАМИ
Из элементов двух множеств можно образовывать новые множества, которые являются результатом определенных операций над множествами. Пересечением множеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А и множеству В. Объединением множеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А 1 или множеству В. При обучении дошкольников действию вычитания воспитатель опирается на понятие дополнения одного множества до другого. Из исходного множества А ребенок удалят подмножество В и считает количество элементов в оставшемся множестве, оно называется дополнением множества В до множества А. 1 Пусть В е А. Дополнением множества В до множества А называется множество, содержащее только те элементы множества А, которые не принадлежат множеству В. Алгебра множеств Алгеброй множеств- называется пара, где — некоторая совокупность множеств, а — набор операций над множествами. Обычно полагают, что — множество всех подмножеств универсума, а в качестве берут рассмотренные выше операции.
Диаграммы Венна Диаграмма Венна четырёх множеств. Собственно «диаграмма Венна» показывает все возможные отношения между множествами или событиями из некоторого семейства. Обычная диаграмма Венна имеет три множества. Сам Венн пытался найти изящный способ с симметричными фигурами, представляющий на диаграмме большее число множеств, но он смог это сделать только для четырех множеств (см. рисунок справа), используя эллипсы.
Диаграммы Эйлера Диаграммы Эйлера аналогичны диаграммам Венна, но не обязательно иллюстрируют все возможные отношения между множествами или событиями.
Основные понятия математической логики
1.Высказывание(суждение)—этоповествовательноепредложение,вкоторомчто-либоутверждаетсяилиотрицается.Поповодулюбоговысказыванияможносказать,истиннооноилиложно.Например:«Лед—твердоесостояниеводы»—истинноевысказывание,6<5—ложноевысказывание. 2.Логическиевеличины:понятия,выражаемыесловами:ИСТИНА,ЛОЖЬ(true,false).Следовательно,истинностьвысказыванийвыражаетсячерезлогическиевеличины. 3.Логическаяконстанта:ИСТИНАилиЛОЖЬ. 4.Логическаяпеременная:символическиобозначеннаялогическаявеличина.Еслиизвестно,чтоА,В,ипр.-переменныелогическиевеличины,тоэтозначит,чтоонимогутприниматьзначениятолькоИСТИНАилиЛОЖЬ. 5.Логическоевыражение—простоеилисложноевысказывание,сложноевысказываниестроитсяизпростыхспомощьюлогическихопераций(связок). 6.Логическаяформула(логическоевыражение)—формула,содержащаялишьлогическиевеличиныизнакилогическихопераций.РезультатомвычислениялогическойформулыявляетсяИСТИНАилиЛОЖЬ Высказывания, операции над высказываниями. Формулы ИВ и таблицы истинности. Логическое следствие и равносильность формул ИВ. Тавтологии. Список основных тавтологий. Множества. Способы задания множеств. Подмножества. Равенство множеств. Пустое множество. Универсальное множество. Теоретико-множественные операции и их свойства. Декартово произведение множеств. Соответствия. Язык стрелок. Виды соответствий. Отображения и их виды. Композиция соответствий и отображений. Ассоциативность композиции. Обратное соответствие и отображение. Критерий обратимости отображения. Алгебраические операции. Арность операции. Свойства бинарных операций. Бинарные отношения и их свойства. Отношение порядка. Виды порядков. Отношение эквивалентности. Свойства классов эквивалентности. Фактор множество. Понятие предиката. Местность предиката Область определения, и область истинности. Кванторы. Формулы ИП. Взаимодействие кванторов и логических связок. Логическая зависимость формул ИП. Предмет комбинаторики. Правила умножения и сложения. Лексико-графический порядок и перебор. Основные комбинаторные соединения. Формулы для подсчета числа размещений, перестановок, размещений с повторениями и сочетаний. Формула для подсчета числа сочетаний с повторениями. Формула бинома. Свойства биномиальных коэффициентов. Треугольник Паскаля. Вычисление количества подмножеств конечного множества. Полиномиальная формула. Разбиения чисел. Разбиения множеств. Числа Стирлинга второго рода. Треугольник Стирлинга. Подсчет количества соответствий, отображений, инъективных отображений, биекций. Метод включения и исключения и подсчет количества субъективных отображений. Связь количества субъективных отображений и чисел Стирлинга второго рода. Числа Белла. Подсчет количества элементов в объединении нескольких множеств. Рекуррентные соотношения. Решение линейных однородных рекуррентных соотношений второго порядка. Рекуррентное и явное задание чисел Фибоначчи. Графы. Пустые и полные графы. Инцидентность, смежность, степени вершин. Лемма о рукопожатиях. Двудольные графы. Подграфы. Изоморфизм графов. Маршруты, пути, простые пути, циклы, простые циклы. Связность. Компоненты связности. Соотношение между количеством ребер, вершин и компонент связности графа. Расстояние в связных графах. Эксцентриситет вершины. Диаметр и радиус графа. Соотношение между диаметром и радиусом. Деревья. Критерии дерева. Эйлеровы графы. Критерий эйлеровости. Гамильтоновы графы. Планарные графы. графы. Формула Эйлера. Непланарность графов K5 и K3,3. Критерий планарности графов. Вершинная и реберная раскраска графов. Хроматическое число и хроматический индекс графа. Проблема четырех красок. Элементы теории Рамсея. Обобщение понятия графа. Псевдографы. Мультиграфы. Орграфы. Бинарные отношения и их свойства с позиций теории графов. Взвешенные графы. Обобщенные графы. Способы задания графов и обобщенных графов. Поиск в глубину в графе. Задачи, решаемые с помощью поиска в глубину. Поиск в ширину в графе. Задачи, решаемые с помощью поиска в ширину. Остов графа. Алгебра логики предусматривает множество логических операций. Однако три из них заслуживают особого внимания, т.к. с их помощью можно описать все остальные, и, следовательно, использовать меньше разнообразных устройств при конструировании схем. Такими операциями являются конъюнкция (И), дизъюнкция (ИЛИ) и отрицание (НЕ). Часто конъюнкцию обозначают &, дизъюнкцию - ||, а отрицание - чертой над переменной, обозначающей высказывание. При конъюнкции истина сложного выражения возникает лишь в случае истинности всех простых выражений, из которых состоит сложное. Во всех остальных случаях сложное выражение будет ложно. При дизъюнкции истина сложного выражения наступает при истинности хотя бы одного входящего в него простого выражения или двух сразу. Бывает, что сложное выражение состоит более, чем из двух простых. В этом случае достаточно, чтобы одно простое было истинным и тогда все высказывание будет истинным. Отрицание – это унарная операция, т.к выполняется по отношению к одному простому выражению или по отношению к результату сложного. В результате отрицания получается новое высказывание, противоположное исходному. Конъюнкция – логическое умножение (И) – and, &, ∧. Дизъюнкция – логическое сложение (ИЛИ) – or, |, v. Логическое отрицание (НЕ) – not,. Действительные числа
Действительные числа образуют совокупность элементов, обладающую следующими свойствами. Если a и b - действительные числа (алгебраические, рациональные, целые, положительные целые), то таковыми же являются и a + b и ab (замкнутость), a + b = b + a, ab = ba (коммутативность), a + (b + c) = (a + b) + c = a + b + c, a(bc) = (ab)c = abc (ассоциативность), a * 1 = a (единица), a(b + c) = ab + ac (дистрибутивность), ;из a + c = b + c следует a = b, из ca = cb,, следует a = b (сокращение). Действительное число 0 (нуль) обладает свойствами a + 0 = a, a * 0 = 0 для каждого действительного числа a. (Единственное) противоположное число -a и (единственное) обратное число a -1 = 1/a для действительного числа a определяются соответственно так: a + (-a) = a - a = 0, aa -1 = 1 (). Помимо "алгебраических" свойств, класс положительных целых, или натуральных, чисел 1, 2,... обладает свойством упорядоченности (n > m, если n = m + x, где x - некоторое натуральное число) и полной упорядоченности (каждое непустое множество натуральных чисел имеет наименьший элемент). Множество натуральных чисел, содержащее число 1 и для каждого из своих элементов n следующий за ним элемент n + 1, содержит все натуральные числа (принцип полной индукции). Свойства натуральных чисел могут быть выведены из пяти аксиом Пеано: 1) 1 есть натуральное число; 2) для каждого натурального числа N существует единственное следующее за ним натуральное число S(n); 3); 4) из S(n) = S(m) следует n = m и 5) имеет место принцип полной индукции. (При его формулировке элемент, следующий за n, обозначается через S(n).) Сложение и умножение, подчиняющиеся правилам (1)-(6), определяются "рекуррентными" соотношениями
n + 1 = S(n), n + S(m) = S(n + m), n*1 = n, n*S(m) = n*m + n.
Целыми числами называются числа вида n, -n и 0, где n - натуральное число, а рациональными - числа вида p/q, где p и q - целые числа и. Действительные числа можно ввести, исходя из множества рациональных чисел, с помощью предельного процесса. Действительные числа, не являющиеся рациональными, называются иррациональными. Действительными алгебраическими числами называются действительные корни алгебраических уравнений с целочисленными коэффициентами, а действительными трансцендентными числами - остальные действительные числа. Класс всех рациональных чисел содержит корни всех линейных уравнений с рациональными коэффициентами и включает в себя все целые числа. Класс всех действительных алгебраических чисел содержит действительные корни всех алгебраических уравнений с алгебраическими коэффициентами и включает в себя все рациональные числа.
5) Функция - одно из основных математических и общенаучных понятий. Оно сыграло и поныне играет большую роль в познании реального мира. Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс.лет назад) пусть несознательно, установили, что площадь круга является функцией от его радиуса посредством нахождения грубо приближенной формулы: S=3r Функции находят широкое применение в экономической теории и практике. Спектр используемых функций весьма широк: от простейших линейных до функций, получаемых по определенному алгоритму с помощью рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени. Наиболее часто используются в экономике следующие функции: 1. Функция полезности (функция предпочтения)- зависимость результата, эффекта некоторого действия от уровня (интенсивности) этого действия. 2. Производственная функция- зависимость результата производственной деятельности от обусловивших его факторов.(Функция выпуска- зависимость объема производства от наличия или потребления ресурсов. Функция издержек- зависимость издержек производства от объема продукции. 3. Функция спроса, потребления и предложения- зависимость объема спроса, потребления или предложения на отдельные товары или услуги от различных факторов(например, цены, дохода и т.п.).
6) Преде́л фу́нкции (предельное значение функции) в заданной точке, предельной для области определения функции, — такая величина, к которой стремится рассматриваемая функция при стремлении её аргумента к данной точке.
Предел функции является обобщением понятия предела последовательности: изначально, под пределом функции в точке понимали предел последовательности элементов области значений функции, составленной из образов точек последовательности элементов области определения функции, сходящейся к заданной точке (предел в которой рассматривается); если такой предел существует, то говорят, что функция сходится к указанному значению; если такого предела не существует, то говорят, что функция расходится. Наиболее часто определение предела функции формулируют на языке окрестностей. То, что предел функции рассматривается только в точках, предельных для области определения функции, означает, что в каждой окрестности данной точки есть точки области определения; это позволяет говорить о стремлении аргумента функции (к данной точке). Но предельная точка области определения не обязана принадлежать самой области определения: например, можно рассматривать предел функции на концах открытого интервала, на котором определена функция (сами концы интервала в область определения не входят). В общем случае необходимо точно указывать способ сходимости функции, для чего вводят т.н. базу подмножеств области определения функции, и тогда формулируют определение предела функции по (заданной) базе. В этом смысле система проколотых окрестностей данной точки — частный случай такой базы множеств. Поскольку на расширенной вещественной прямой можно построить базу окрестностей бесконечно удалённой точки, то оказывается допустимым описание предела функции при стремлении аргумента к бесконечности, а, также, описание ситуации, когда функция сама стремится к бесконечности (в заданной точке). Предел последовательности (как предел функции натурального аргумента), как раз предоставляет пример сходимости по базе «стремление аргумента к бесконечности». Отсутствие предела функции (в данной точке) означает, что для любого заранее заданного значения области значений и всякой его окрестности сколь угодно близко от заданной точки существуют точки, значение функции в которых окажется за пределами заданной окрестности. Если в некоторой точке области определения функции существует предел и этот предел равен значению в данной функции, то функция оказывается непрерывной (в данной точке).
Пределы на бесконечности Предел функции на бесконечности описывает поведение значения данной функции, когда её аргумент становится бесконечно большим. Существуют различные определения таких пределов, но они эквивалентны между собой.
Предел на бесконечности по Гейне Пусть числовая функция задана на множестве, в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка. В этом случае число называется пределом функции на бесконечности, если для всякой бесконечно большой последовательности точек соответствующая последовательность частных значений функции в этих точках сходится к числу. Пусть числовая функция задана на множестве, в котором для любого числа найдётся элемент, лежащий правее него. В этом случае число называется пределом функции на плюс бесконечности, если для всякой бесконечно большой последовательности положительных точек соответствующая последовательность частных значений функции в этих точках сходится к числу. Пусть числовая функция задана на множестве, в котором для любого числа найдётся элемент, лежащий левее него. В этом случае число называется пределом функции на минус бесконечности, если для всякой бесконечно большой последовательности отрицательных точек соответствующая последовательность частных значений функции в этих точках сходится к числу.
Предел на бесконечности по Коши Пусть числовая функция задана на множестве, в котором отыщется сколь угодно большой элемент, то есть для всякого положительного в нём найдётся элемент, лежащий за границами отрезка. В этом случае число называется пределом функции на бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, превышающих по абсолютному значению, справедливо неравенство. Пусть числовая функция задана на множестве, в котором для любого числа найдётся элемент, лежащий правее него. В этом случае число называется пределом функции на плюс бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, лежащих правее, справедливо неравенство. Пусть числовая функция задана на множестве, в котором для любого числа найдётся элемент, лежащий левее него. В этом случае число называется пределом функции на минус бесконечности, если для произвольного положительного числа отыщется отвечающее ему положительное число такое, что для всех точек, лежащих левее, справедливо неравенство. Бесконечно малая величина Последовательность an называется бесконечно малой, если. Например, последовательность чисел — бесконечно малая. Функция называется бесконечно малой в окрестности точки x0, если. Функция называется бесконечно малой на бесконечности, если либо. Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если, то f(x) − a = α(x),.
Бесконечно большая величина Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsin x, неограниченная с обеих сторон, не является бесконечно большой при. Последовательность an называется бесконечно большой, если. Функция называется бесконечно большой в окрестности точки x0, если. Функция называется бесконечно большой на бесконечности, если либо. [править] Свойства бесконечно малых Сумма конечного числа бесконечно малых — бесконечно малая. Произведение бесконечно малых — бесконечно малая. Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая. Если an — бесконечно малая последовательность, сохраняющая знак, то — бесконечно большая последовательность.
Первый замечательный предел Рассмотрим следующий предел: (вместо родной буквы «хэ» я буду использовать греческую букву «альфа», это удобнее с точки зрения подачи материала). Согласно нашему правилу нахождения пределов (см. статью Пределы. Примеры решений) пробуем подставить ноль в функцию: в числителе у нас получается ноль (синус нуля равен нулю), в знаменателе, очевидно, тоже ноль. Таким образом, мы сталкиваемся с неопределенностью вида, которую, к счастью, раскрывать не нужно. В курсе математического анализа, доказывается, что: Данный математический факт носит название Первого замечательного предела. Нередко в практических заданиях функции могут быть расположены по-другому, это ничего не меняет: – тот же самый первый замечательный предел. Но самостоятельно переставлять числитель и знаменатель нельзя! Если дан предел в виде, то и решать его нужно в таком же виде, ничего не переставляя. На практике в качестве параметра может выступать не только переменная, но и элементарная функция, сложная функция. Важно лишь, чтобы она стремилась к нулю.
Второй замечательный предел В теории математического анализа доказано, что: Данный факт носит название второго замечательного предела. Справка: – это иррациональное число. В качестве параметра может выступать не только переменная, но и сложная функция. Важно лишь, чтобы она стремилась к бесконечности. 12) Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.
Экономический смысл производной. Если спросить экономиста “Что такое производная?”, то он ответит: «маржинализм». Слово «маржинализм» охватывает целый комплекс понятий в современной экономической науке. В ХIХ в. в области экономической теории произошло событие, которое впоследствии привело к подлинному перевороту в методах экономического поведения людей или фирм, изменило характер научно-экономического мышления. Классическая наука обычно имела дело со средними величинами: средняя цена, средняя производительность труда и т.д. Но постепенно сложился иной подход к анализу экономических процессов и явлений. Во второй половине ХIХ в. была сформулирована теория маржинализма. Классиками этой теории стали экономисты австрийской школы К. Менгер (1840-1921), Ф. фон Визер (1851-1926), Е. фон Бём-Баверк (1851-1914), а также английский экономист У.С. Джевонс (1835-1882). "Marginal" в переводе с английского языка означает "находящийся на самом краю", "предельный", "граничный". К предельным величинам в экономике относятся: предельные издержки, предельный доход, предельная полезность, предельная производительность, предельная склонность к потреблению и т.д. Понятие предельных величин позволило создать совершенно новый инструмент исследования и описания экономических явлений, посредством которого стало возможно решать научные проблемы, прежде не решённые или решённые неудовлетворительно. Все эти величины самым тесным образом связаны с понятием производной. Предельные величины характеризуют не состояние (как суммарная или средняя величины), а процесс, изменение экономического объекта. Следовательно, производная выступает как скорость изменения некоторого экономического объекта (процесса) с течением времени или относительно другого исследуемого фактора. Конечно, экономика не всегда позволяет использовать предельные величины в силу неделимости многих экономических расчетов, а также прерывности (дискретности) экономических показателей во времени (например, годовых, квартальных, месячных и т.д.). В то же время во многих случаях можно эффективно использовать предельные величины Рассмотрим ситуацию: пусть q – количество произведённой продукции, ТC(q) – соответствующие данному выпуску совокупные издержки (total costs), тогда q – прирост продукции, а ТС – прирост издержек производства. Предельные издержки МС (marginal costs) выражают дополнительные затраты на производство каждой дополнительной единицы продукции. Другими словами,где Используя равенство получим Итак, предельные издержки есть не что иное, как первая производная от совокупных издержек, если последние представлены как функция от выпускаемого количества продукции. Аналогичным образом определяются и многие другие экономические величины, имеющие предельный характер. Предельная выручка MR (marginal revenue) – это дополнительный доход, полученный при переходе от производства n-ной к (n+1)-ой единице продукта. Она представляет собой первую производную от выручки: Для хозяйствующего субъекта, который действует в условиях совершенной конкуренции: TR = P*Q, где TR – выручка (total revenue); P – цена (price). Таким образом, MR= P. Это равенство верно для рынка совершенной конкуренции. Любой индивид использует свой доход Y после уплаты налогов на потребление C и сбережение S. Ясно, что лица с низким доходом целиком используют его на потребление, а на сбережение средств не остается. С ростом дохода субъект не только больше потребляет, но и больше сберегает. Как установлено экономической наукой, потребление и сбережение зависят от размера дохода: Y= C(Y) + S(Y). Использование производной позволяет определить такую категорию, как предельную склонность к потреблению MPC (marginal property to consume), показывающую долю прироста личного потребления в приросте дохода: По мере увеличения доходов MPC уменьшается. Долю прироста сбережений в приросте дохода показывает предельная склонность к сбережению MPS (marginal propensity to save): С увеличением доходов MPS увеличивается. Поскольку ограниченность ресурсов принципиально не устранима, то решающее значение приобретает отдача от факторов производства. Здесь также применима производная, как инструмент исследования. Пусть применяемый капитал постоянен, а затраты труда увеличиваются. Можно ввести в экономический анализ следующую категорию – предельный продукт труда MPL (marginal product of labor) – это дополнительный продукт, полученный в результате дополнительных вложений труда при неизменной величине капитала: Если вложения осуществляются достаточно малыми порциями, то так как dY - результат, dL - затраты, то MPL – предельная производительность труда. Аналогично, MPK (marginal product of capital) – предельный продукт капитала – дополнительный продукт, полученный в результате дополнительных вложений капитала K при неизменной величине труда: Если вложения осуществляются малыми порциями, то MPk характеризует предельную производительность капитала. Категория предельной полезности MU (marginal utility) выражает дополнительную полезность от каждой дополнительной потреблённой единицы блага При бесконечно малых изменениях предельная полезность есть производная от совокупной полезности, которая представлена как функция от потребляемого количества продукта.
13) Производные элементарных функций.
Производная сложной функции. Функции сложного вида не совсем корректно называть термином «сложная функция». К примеру, смотрится очень внушительно, но сложной эта функция не является, в отличие от. В этой статье мы разберемся с понятием сложной функции, научимся выявлять ее в составе элементарных функций, дадим формулу нахождения ее производной и подробно рассмотрим решение характерных примеров. При решении примеров будем постоянно использовать таблицу производных и правила дифференцирования, так что держите их перед глазами. Сложная функция – это функция, аргументом которой также является функция. С нашей точки зрения, это определение наиболее понятно. Условно можно обозначать как f(g(x)). То есть, g(x) как бы аргумент функции f(g(x)). К примеру, пусть f – функция арктангенса, а g(x) = lnx есть функция натурального логарифма, тогда сложная функция f(g(x)) представляет собой arctg(lnx). Еще пример: f – функция возведения в четвертую степень, а - целая рациональная функция (смотрите классификацию элементарных функций), тогда. В свою очередь, g(x) также может быть сложной функцией. Например,. Условно такое выражение можно обозначить как. Здесь f – функция синуса, - функция извлечения квадратного корня, - дробная рациональная функция. Логично предположить, что степень вложенности функций может быть любым конечным натуральным числом. Часто можно слышать, что сложную функцию называют композицией функций. Формула нахождения производной сложной функции.
Асимптоты графика функции Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и горизонтальная.
Вертикальная Вертикальная асимптота — прямая вида при условии существования предела. Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
Горизонтальная Горизонтальная асимптота — прямая вида при условии существования предела
Перестановки без повторений комбинаторика множество сумма повторение В случае n = m (см. размещения без повторений) из n элементов по m называется перестановкой множества x. Количество всех перестановок из n элементов обозначают Pn. Pn = n! Действительно при n = m.
Размещения без повторений 1. Сколько можно составить телефонных номеров из 6 цифр каждый, так чтобы все цифры были различны? Это пример задачи на размещение без повторений. Размещаются здесь 10 цифр по 6. А варианты, при которых одинаковые цифры стоят в разном порядке считаются разными. Если X-множество, состоящие из n элементов, m?n, то размещением без повторений из n элементов множества X по m называется упорядоченное множество X, содержащее m элементов называется упорядоченное множество X, содержащее m элементов. Количество всех размещений из n элементов по m обозначают n! – n-факториал (factorial анг. сомножитель) произведение чисел натурального ряда от 1 до какого либо числа n n! = 1*2*3*...*n 0! = 1 Значит, ответ на вышепоставленную задачу будет… 2. Сколькими способами 4 юноши могут пригласить четырех из шести девушек на танец? Решение: два юноши не могут одновременно пригласить одну и ту же девушку. И варианты, при которых одни и те же девушки танцуют с разными юношами считаются, разными, поэтому возможно 360 вариантов.
Сочетания без повторений Сочетанием без повторений называется такое размещение, при котором порядок следования элементов не имеет значения. Всякое подмножество X состоящее из m элементов, называется сочетанием из n элементов по m. Таким образом, количество вариантов при сочетании будет меньше количества размещений. Число сочетаний из n элементов по m обозначается.
Формула Бернулли Формула Бернулли — формула в теории вероятностей, позволяющая находить вероятность появления события A при независимых испытаниях. Формула Бернулли позволяет избавиться от большого числа вычислений — сложения и умножения вероятностей — при достаточно большом количестве испытаний. Названа в честь выдающегося швейцарского математика Якоба Бернулли, выведшего формулу.
Теорема: Если Вероятность p наступления события Α в каждом испытании постоянна, то вероятность Pk,n того, что событие A наступит k раз в n независимых испытаниях, равна:
Основные понятия математической статистики. Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений. Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений. Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть: - оценка неизвестной вероятности события; - оценка параметров распределения случайной величины; - оценка неизвестной функции распределения случайной величины; - проверка гипотез о параметрах распределения или о виде неизвестного распределения; - оценка зависимости случайной величины от одной или нескольких случайных величин и т.д. Случайную величину Исходным материалом для изучения свойств генеральной совокупности Набор Совокупность чисел
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 935; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.148 (0.022 с.) |


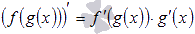
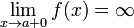
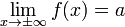
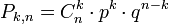 , где q = 1-р
, где q = 1-р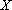 будем называть генеральной совокупностью.
будем называть генеральной совокупностью.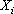 ,
,  , заданной на множестве исходов
, заданной на множестве исходов  -го опыта, не зависит от
-го опыта, не зависит от  независимых в совокупности случайных величин
независимых в совокупности случайных величин  , где
, где  , полученных в результате
, полученных в результате 


