
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула полной вероятности и формула Байеса.Содержание книги
Поиск на нашем сайте Если событие события Проиллюстрируем формулу полной вероятности на графе с выделенной вершиной:
Полная вероятность события равна весу всего вероятностного графа с гипотезами. С формулой полной вероятности тесно связана формула Байеса. Если до опыта вероятности гипотез были
Формула Байеса дает возможность "пересмотреть" вероятность гипотез с учетом наблюдавшегося результата опыта. Условная вероятность как отношение веса ветви, проходящей через вершину, соответствующую гипотезе
Основные понятия математической статистики. Математическая статистика – это наука, изучающая случайные явления посредством обработки и анализа результатов наблюдений и измерений. Первая задача математической статистики – указать способы получения, группировки и обработки статистических данных, собранных в результате наблюдений, специально поставленных опытов или произведённых измерений. Вторая задача математической статистики – разработка методов анализа статистических сведений в зависимости от целей исследования. Например, целью исследования может быть: - оценка неизвестной вероятности события; - оценка параметров распределения случайной величины; - оценка неизвестной функции распределения случайной величины; - проверка гипотез о параметрах распределения или о виде неизвестного распределения; - оценка зависимости случайной величины от одной или нескольких случайных величин и т.д. Случайную величину Исходным материалом для изучения свойств генеральной совокупности Набор Совокупность чисел В основе большинства результатов математической статистики лежит выборочный метод, состоящий в том, что свойства генеральной совокупности устанавливаются путём изучения тех же свойств на случайной выборке.
Математи́ческое ожида́ние — среднее значение случайной величины, распределение вероятностей случайной величины, рассматривается в теории вероятностей. В англоязычной литературе и в математическом сообществе Санкт-Петербурга обозначается через
Дисперсия, в математической статистике и теории вероятностей, наиболее употребительная мера рассеивания, т. е. отклонения от среднего. В статистическом понимании Дисперсии.
Дисперсия вычисляется по формуле
Среднее квадратичное отклонение — это квадратный корень из среднего арифметического всех квадратов разностей между данными величинами и их средним арифметическим. Среднее квадратичное отклонение принято обозначать греческой буквой сигма σ
|
||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 386; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

 может наступить только при появлении одного из несовместных событий (гипотез)
может наступить только при появлении одного из несовместных событий (гипотез)  , то вероятность события вычисляется по формуле полной вероятности:
, то вероятность события вычисляется по формуле полной вероятности:  , где -вероятность гипотезы
, где -вероятность гипотезы 
 ,
,  - условная вероятность
- условная вероятность

 ,
,  ,..
,..  .,, а в результате опыта появилось событие, то с учетом этого события "новые", т.е. условные вероятности гипотез вычисляются по формуле Байеса
.,, а в результате опыта появилось событие, то с учетом этого события "новые", т.е. условные вероятности гипотез вычисляются по формуле Байеса
 может находиться
может находиться , к весу всего вероятностного графа.
, к весу всего вероятностного графа.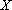 будем называть генеральной совокупностью.
будем называть генеральной совокупностью.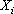 ,
,  , заданной на множестве исходов
, заданной на множестве исходов  -го опыта, не зависит от
-го опыта, не зависит от  независимых в совокупности случайных величин
независимых в совокупности случайных величин  , где
, где  , полученных в результате
, полученных в результате  в русской — M[X] (возможно, от англ. Mean value или нем. Mittelwert, а возможно от рус. Математическое ожидание). В статистике часто используют обозначение μ.
в русской — M[X] (возможно, от англ. Mean value или нем. Mittelwert, а возможно от рус. Математическое ожидание). В статистике часто используют обозначение μ.






