
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные элементарные функцииСодержание книги Поиск на нашем сайте
Аналитический способ Обычно функция задаётся с помощью формулы, в которую входят переменные, операции и элементарные функции. Возможно, кусочное задание, то есть различное для различных значений аргумента. Примеры: § § § § Табличный способ Функцию можно задать, перечислив все её возможные аргументы и значения для них. После этого, если это необходимо, функцию можно доопределить для аргументов, которых нет в таблице, путём интерполяции или экстраполяции. Примерами могут служить программа передач, расписание поездов или таблица значений булевой функции:
Графический способ
Функцию можно задать графически, отобразив множество точек её графика на плоскости. Это может быть приблизительный набросок, как должна выглядеть функция, или показания, снятые с прибора, например, с осциллографа. Этот способ задания может страдать от недостаткаточности, однако в некоторых случаях другие способы задания вообще не могут быть применены. Кроме того, такой способ задания один из самых презентативных, удобных для восприятия и качественного эвристического анализа функции. Рекурсивный способ Функция может быть задана рекурсивно, то есть через саму себя. В этом случае одни значения функции определяются через другие её значения. Примеры: § факториал; § числа Фибоначчи; § функция Аккермана. Словесный способ Функцию можно описать словами на естественном языке каким-либо однозначным способом, например, описав её входные и выходные значения, или алгоритм, с помощью которого функция задаёт соответствия между этими значениями. Наряду с графическим способом, иногда это единственный способ описать функцию, хотя естественные языки и не столь детерминированы, как формальные. Примеры: Факториал § Возвращает произведение всех натуральных чисел, не больших данного. Кроме того,
§ Область определения: § Область значений:
2) Функция, непрерывная на отрезке (или любом другом компактном множестве), равномерно непрерывна на нём. Функция, непрерывная на отрезке (или любом другом компактном множестве), ограничена и достигает на нём свои максимальное и минимальное значения. Областью значений функции Если функция Если функция § Непрерывное отображение отрезка в вещественную прямую инъективно в том и только в том случае, когда данная функция на отрезке строго монотонна. § Монотонная функция на отрезке § Если функции Примеры Элементарные функции Произвольные многочлены, рациональные функции, показательные функции, логарифмы, тригонометрические функции (прямые и обратные) непрерывны везде в своей области определения. [править]Функция с устранимым разрывом Функция
непрерывна в любой точке
[править]Функция знака Функция
называется функцией знака. Эта функция непрерывна в каждой точке Точка x = 0 является точкой разрыва первого рода, причём
в то время как в самой точке функция обращается в нуль. Ступенчатая функция Ступенчатая функция, определяемая как
является всюду непрерывной, кроме точки x = 0, где функция терпит разрыв первого рода. Тем не менее, в точке x = 0 существует правосторонний предел, который совпадает со значением функции в данной точке. Таким образом, ступенчатая функция является примером непрерывной справа функции на всей области определения. Аналогично, ступенчатая функция, определяемая как
является примером непрерывной слева функции на всей области определения.
3) Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
Бесконечно малая величина Последовательность an называется бесконечно малой, если Функция называется бесконечно малой в окрестности точки x 0, если Функция называется бесконечно малой на бесконечности, если Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если Если an — бесконечно малая последовательность, сохраняющая знак, то § Бесконечно большая величина § Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция x sin x, неограниченная с обеих сторон, не является бесконечно большой при § Последовательность an называется бесконечно большой, если § Функция называется бесконечно большой в окрестности точки x 0, если § Функция называется бесконечно большой на бесконечности, если
связь между бесконечно малыми и большими функциями Если f (x) — бесконечно большая функция, то § ( Так как | f (x)| > K, то ( § Это означает, что
Свойства бесконечно малых § Сумма конечного числа бесконечно малых — бесконечно малая. § Произведение бесконечно малых — бесконечно малая. § Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая. § Если an — бесконечно малая последовательность, сохраняющая знак, то
является бесконечно малой при
представляет собой бесконечно малую при
7) Сходящиеся последовательности и их свойства Рассмотрим числовые последовательности. Последовательность (xn) действительных чисел называется сходящейся, если существует действительное число a и для произвольного ε > 0 существует натуральное число m такое, что для всех n > m справедливо неравенство | xn - a | < ε. При этом число a называют пределом последовательности (xn), что символически записывают
С помощью логических символов определение запишется следующим образом: числовая последовательность (xn) называется сходящейся, если
Если последовательность не является сходящейся, то ее называют расходящейся. Если последовательности (xn) и (yn) действительных чисел сходятся и
8) Необходимый признак сходимости последовательности. Необходимое и достаточное условия сходимости монотонной последовательности. Примеры
9) Пусть имеется множество Последовательность
Последовательность
Последовательность
Последовательность
Последовательность называется монотонной, если она является неубывающей, либо невозрастающей.[1] Последовательность называется строго монотонной, если она является возрастающей, либо убывающей. Очевидно, что строго монотонная последовательность является монотонной. Иногда используется вариант терминологии, в котором термин «возрастающая последовательность» рассматривается в качестве синонима термина «неубывающая последовательность», а термин «убывающая последовательность» — в качестве синонима термина «невозрастающая последовательность». В таком случае возрастающие и убывающие последовательности из вышеприведённого определения называются «строго возрастающими» и «строго убывающими», соответственно. Число эйлера e — математическая константа, основание натурального логарифма, трансцендентное число. Иногда число e называют числомЭйлера или числом Непера. Обозначается строчной латинской буквой «e». Численное значение[1]:
Число e играет важную роль в дифференциальном и интегральном исчислении, а также во многих других разделах математики. Способы определения Число e может быть определено несколькими способами. § Через предел:
§ Как сумма ряда:
§ Как единственное число a, для которого выполняется
§ Как единственное положительное число a, для которого верно
Свойства § § Число e иррационально и даже трансцендентно. Его трансцендентность была доказана только в 1873 году Шарлем Эрмитом. Предполагается, что e — нормальное число, то есть вероятность появления разных цифр в его записи одинакова. § Число e является вычислимым (а значит, и арифметическим) числом. § § § Ещё одна формула, связывающая числа е и π, т. н. «интеграл Пуассона» или «интеграл Гаусса»
§ Для любого комплексного числа z верны следующие равенства:
§ Представление Каталана:
§ Мера иррациональности (англ.) числа e равна 2 (что есть наименьшее возможное значение для иррациональных чисел).
Второй замечательный предел Второй замечательный предел имеет вид:
или в другой записи
В случае второго замечательного предела имеем дело с неопределенностью вида единица в степени бесконечность
Вычислить предел Решение. Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность. Смотрим в таблицу неопределенностей для определения метода решения и останавливаемся на применении второго замечательного предела. Сделаем замену переменных. Пусть
Если Исходный предел после замены примет вид:
Ответ:
Вычислить предел Решение. Подставляем бесконечность:
Пришли к неопределенности единица в степени бесконечность, которая указывает на применение второго замечательного предела. Выделим целую часть в основании показательно степенной функции:
Тогда предел запишется в виде:
Сделаем замену переменных. Пусть
Если Исходный предел после замены примет вид:
В преобразованиях были использованы свойства степени и свойства пределов. Ответ:
10) Предел функции по Коши Значение
Точки разрыва Если попытаться построить отрицание свойства непрерывности функции в точке (предельной для области определения), то получится следующее. Существует такая окрестность значения функции в рассматриваемой точке, что сколь близко мы не подходили бы к данной точке, всегда можно будет найти точку, значение в которой окажется за пределами заданной окрестности. В этом случае говорят, что функция f терпит разрыв в точке a.
Возможны два варианта: § либо предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка a называется точкой устранимого разрыва функции f (в комплексном анализе — устранимая особая точка). Положив § либо предела функции в данной точке не существует. В этом случае для числовой функции, заданной на вещественной прямой (или её подмножестве), возможно существование односторонних пределов. Отсюда возникает классификация точек (неустранимого) разрыва: § если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода; § если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. Точка, в которой функция не определена, будет точкой разрыва функции лишь при условии, если функция определена, хотя бы с одной стороны вблизи этой точки.
Рис. 2 Придав произвольное приращение аргументу Касательной к графику функции Для того, чтобы секущая Угловой коэффициент касательной получается путем перехода от
Таким образом, получим, что
В случае бесконечной производной Из уравнения секущей имеем:
Переходя в равенстве к пределу при Примеры задач Задача 1. Составьте уравнение общей касательной к графикам функций Решение. I способ. Прямая
Решением системы будут
Примеры. 1. Составить уравнения касательной и нормали к графику функции у = tg 2 x в точке с абсциссой x 0 =π/4.
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4 x – π + 1. Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4· x + π/16 + 1. 2. Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2) 2 + 5 в точке M (2; 5). y '= x – 2, y '(2) = 0. Следовательно, касательная параллельна оси Ox, а значит ее уравнение y = 5. Тогда нормаль параллельна оси Oy и имеет уравнение x = 2. 3. Найти уравнение касательной и нормали к эллипсу Найдем y ' по правилу дифференцирования неявной функции Уравнение касательной: Уравнение нормали: 4. Составить уравнения касательной и нормали к циклоиде x = t – sin t, y = 1 – cos t в точке М (x 0; y 0), которая соответствует значению параметра t = π/2. При t =π/2 x 0 = π/2 – 1, y 0 =1.
Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2. Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.
Правила дифференцирования Если функции f и g дифференцируемы в точке
Доказательство а) Постоянный множитель C можно выносить из-под знака производной: В частности, б) Функцию f · g можно записать в виде в) Для доказательства этой формулы заметим, что Если f дифференцируема, то Доказательство этой формулы предоставляем читателю. Если функция y = f (x) непрерывна и строго возрастает в окрестности точки Если функции y = f (x) и z = g (y) дифференцируемы в точках x 0 и y 0 = f (x 0) соответственно, то сложная функция z = g (f (x)) дифференцируема в точкеx 0, причем Следствием этой теоремы является тот факт, что дифференциал функции y = f (x) имеет один и тот же вид Если f (x) – четная функция, то Пусть в окрестности точки t 0 определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна. Пусть в этой окрестности существуют производные 18) Понятие дифференциала и его геометрический смысл Пусть функция | |||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

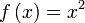 ;
;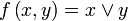 ;
;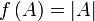 ;
;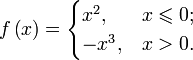
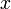
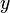
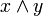
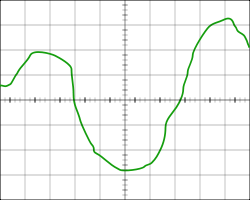
 Осциллограмма задаёт значение некоторой функции графически.
Осциллограмма задаёт значение некоторой функции графически.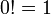 .
.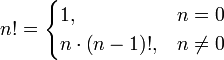
 (множество натуральных чисел с нулём).
(множество натуральных чисел с нулём).
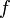 , непрерывной на отрезке
, непрерывной на отрезке 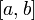 , является отрезок
, является отрезок 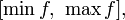 где минимум и максимум берутся по отрезку
где минимум и максимум берутся по отрезку 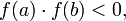 то существует точка
то существует точка 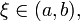 в которой
в которой 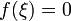 .
.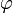 удовлетворяет неравенству
удовлетворяет неравенству 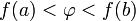 или неравенству
или неравенству 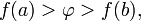 то существует точка
то существует точка 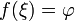 .
.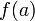 и
и 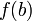 .
.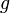 непрерывны на отрезке
непрерывны на отрезке 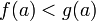 и
и 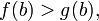 то существует точка
то существует точка 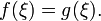 Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.
Отсюда, в частности, следует, что любое непрерывное отображение отрезка в себя имеет хотя бы одну неподвижную точку.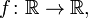 задаваемая формулой
задаваемая формулой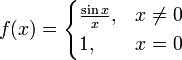
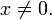 Точка x = 0 является точкой устранимого разрыва, ибо предел функции
Точка x = 0 является точкой устранимого разрыва, ибо предел функции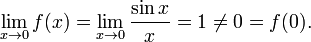
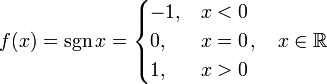
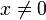 .
.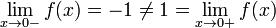 ,
,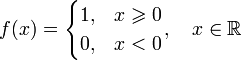
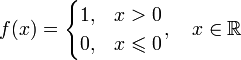
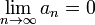 . Например, последовательность чисел
. Например, последовательность чисел 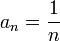 — бесконечно малая.
— бесконечно малая.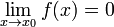 .
.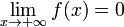 либо
либо 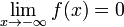 .
.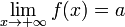 , то f (x) − a = α(x),
, то f (x) − a = α(x), 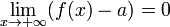 .
.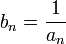 — бесконечно большая последовательность.
— бесконечно большая последовательность.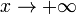 .
.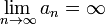 .
.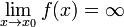 .
.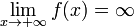 либо
либо 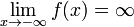
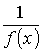 есть бесконечно малая функция в этой же точке.
есть бесконечно малая функция в этой же точке.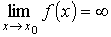 , это означает, что
, это означает, что K > 0) (
K > 0) (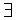 δ = δ(K)> 0) (
δ = δ(K)> 0) (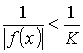 .
. 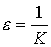 , тогда
, тогда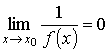 .
.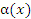 при
при 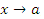 и функции
и функции  , ограниченной в некоторой
, ограниченной в некоторой 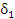 -окрестности точки a, есть функция бесконечно малая. Доказательство. Функция
-окрестности точки a, есть функция бесконечно малая. Доказательство. Функция 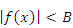
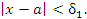
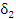 , что неравенство
, что неравенство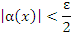
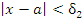
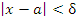
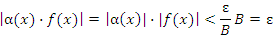
 – бесконечно малые функции при
– бесконечно малые функции при  . Тогда существуют такие положительные числа
. Тогда существуют такие положительные числа 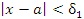
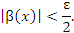
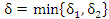 , то условие
, то условие 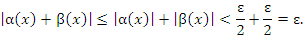
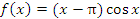
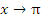 , поскольку представляет собой произведение ограниченной функции
, поскольку представляет собой произведение ограниченной функции 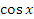 и бесконечно малой
и бесконечно малой 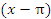 .
.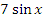 является бесконечно малой при
является бесконечно малой при 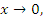 , ибо
, ибо 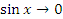 при
при 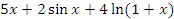
 или xn → a при n → ∞.
или xn → a при n → ∞.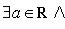
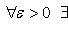
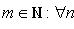
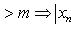
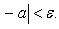
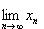
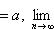
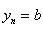 , то
, то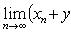
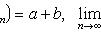
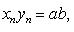
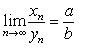
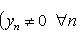
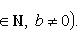
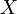 , на котором введено отношение порядка.
, на котором введено отношение порядка.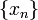 элементов множества
элементов множества 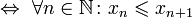
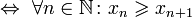
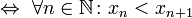

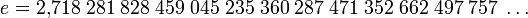 (последовательность A001113 вOEIS)
(последовательность A001113 вOEIS)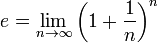 (второй замечательный предел).
(второй замечательный предел).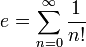 или
или 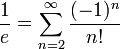 .
.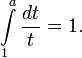
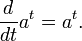

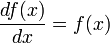 является функция
является функция 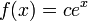 , где c — произвольная константа.
, где c — произвольная константа.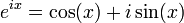 , см. формула Эйлера, в частности
, см. формула Эйлера, в частности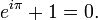
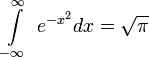
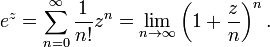
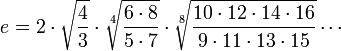
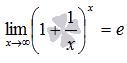
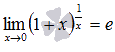
 .
.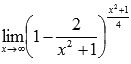
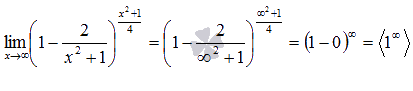
 , то
, то 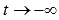
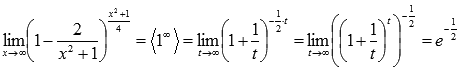
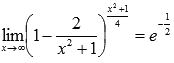
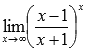
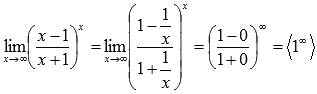
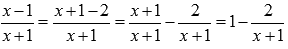
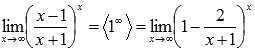
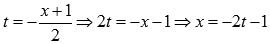
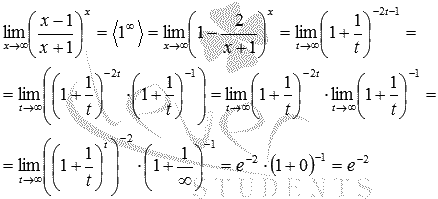
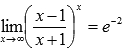
 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции 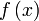 в точке
в точке  , если для любого наперёд взятого положительного числа ε найдётся отвечающее ему положительное число
, если для любого наперёд взятого положительного числа ε найдётся отвечающее ему положительное число 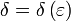 такое, что для всех аргументов
такое, что для всех аргументов 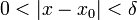 , выполняется неравенство
, выполняется неравенство 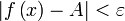 .[1]
.[1]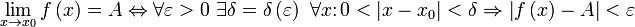


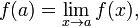 можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности. , так чтобы
, так чтобы  , перейдем к точке
, перейдем к точке  с абсциссой
с абсциссой  и ординатой
и ординатой  , где
, где  Уравнение прямой, проходящей через точки
Уравнение прямой, проходящей через точки  и
и  , имеет вид:
, имеет вид:  , где отношение
, где отношение 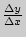 представляет собой угловой коэффициент секущей (
представляет собой угловой коэффициент секущей ( .
. в точке
в точке  , при стремлении точки
, при стремлении точки  стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел
стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел  , то есть, чтобы существовала конечная производная функции
, то есть, чтобы существовала конечная производная функции  в точке
в точке  .
.
 , где
, где  - угол наклона касательной к оси
- угол наклона касательной к оси  (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции
(см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции 
 .
.
 , то есть касательная является в данном случае вертикальной прямой, проходящей через точку
, то есть касательная является в данном случае вертикальной прямой, проходящей через точку  и
и  .
. является общей касательной графиков функций
является общей касательной графиков функций  и
и  , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.
, если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке. - уравнение касательной к графику функции y=x2 в точке с абсциссой x0
- уравнение касательной к графику функции y=x2 в точке с абсциссой x0 - уравнение касательной к графику функции y=x3 в точке с абсциссой x1
- уравнение касательной к графику функции y=x3 в точке с абсциссой x1

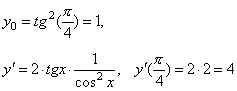
 в точке M (2; 3).
в точке M (2; 3). .
. ,т.е.
,т.е.  .
. , т.е.
, т.е.  .
. .
. то в этой же точке дифференцируемы сумма, произведение и частное (если
то в этой же точке дифференцируемы сумма, произведение и частное (если  ) этих функций, причем
) этих функций, причем


 По свойству предела суммы получаем
По свойству предела суммы получаем 


 Но
Но  По свойству предела произведения получаем
По свойству предела произведения получаем  Используя доказанное равенство, получим, что
Используя доказанное равенство, получим, что  Раскрывая скобки и приводя подобные члены, получим формулу
Раскрывая скобки и приводя подобные члены, получим формулу 
 Воспользовавшись свойством предела частного, получим
Воспользовавшись свойством предела частного, получим  После этого представим
После этого представим  как произведение функций f и
как произведение функций f и  откуда и следует доказываемая формула.
откуда и следует доказываемая формула. где
где  также дифференцируема, причем
также дифференцируема, причем 
 то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем
то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем 

 как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.
как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного. – нечетная; если f (x) – нечетная функция, то
– нечетная; если f (x) – нечетная функция, то  и
и  Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем
Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем 
 определена на промежутке
определена на промежутке 


