
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Выпуклость функции и точки перегибаСодержание книги Поиск на нашем сайте
Непрерывная на отрезке [ a; b ] функция f (x) называется выпуклой вверх на этом отрезке, если для любых точек x 1 и x 2 из этого отрезка
Другими словами, если для любых точек x 1 и x 2 отрезка [ a; b ] секущая AB проходит под графиком функции f (x), то функция f выпукла вверх. Аналогично определяется функция, выпуклая вниз. Дважды дифференцируемая на [ a; b ] функция f (x) выпукла вверх, если для любого
Дважды дифференцируемая на [ a; b ] функция f (x) выпукла вниз, если для любого
Так, вторая производная функции Пусть функция f (x) непрерывна в точке Необходимое условие наличия точки перегиба. Если
Достаточные условия наличия точки перегиба. Пусть функция f (x) непрерывна и имеет конечную или бесконечную производную в точке Если
В заключение приведем примеры, когда точка x 0 не является точкой перегиба несмотря на то, что ее вторая производная меняет знак при переходе через эту точку:
Не являются точками перегиба и точки возврата, например точка Все вышеперечисленные случаи изображены на рисунке.
Асимптоты графика функции Назовём асимптотами прямые линии, к которым неограниченно приближается график функции, когда точка графика неограниченно удаляется от начала координат. В зависимости от поведения аргумента при этом, различаются два вида асимптот: вертикальные и наклонные. Определение 7.1 Вертикальной асимптотой графика функции
Пример 7.1 Рассмотрим функцию
Рис.7.1.Вертикальная асимптота функции
Пример 7.2 Рассмотрим функцию
Рис.7.2.Вертикальная асимптота функции
Пример 7.3 Рассмотрим функцию
Рис.7.3.Вертикальная асимптота функции
Итак, для нахождения вертикальных асимптот графика данной функции нужно исследовать точки разрыва функции и точки, лежащие на границах области определения функции, и выяснить, при приближении аргумента к каким из этих точек значения функции стремятся к бесконечности. Наклонной асимптотой графика функции
Наклонной асимптотой графика функции
Рис.7.6.Графики функций, имеющие наклонные асимптоты при
В случае, если наклонная асимптота расположена горизонтально, то есть при
или
соответственно. Пример 7.6 Рассмотрим функцию
Однако эта функция не определена ни на каком луче вида
Рис.7.7.Наклонная асимптота функции
Пример 7.7 График функции
Аналогично определению наклонной асимптоты можно дать также более общее определение: Определение 7.3 Линия Если функция Пример 7.9 Рассмотрим функцию
Рис.7.10.Асимптотическая линия
Вернёмся к наклонным асимптотам -- прямым линиям с уравнением Теорема 7.1 Прямая
И
(соответственно, если
Таким образом, для нахождения наклонной (или горизонтальной, если получится Доказательство теоремы. Докажем теорему в случае Перепишем условие (7.1), задающее асимптоту, в виде
Так как первый множитель
Но
откуда следует равенство (7.2). Теперь число Подставляя это число в формулу (7.1), находим, что
откуда следует равенство (7.3).
Пример 7.10 Найдём наклонные асимптоты графика Попробуем отыскивать сразу оба предела, и при
Итак, и при
Рис.7.11.График
Замечание 7.2 Из определения асимптоты не следует, что если асимптоты при Пример 7.11 Рассмотрим график
Рис.7.12.График арктангенса имеет две разных горизонтальных асимптоты
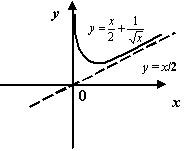
Различными могут оказаться и не обязательно горизонтальные асимптоты: Пример 7.12 Рассмотрим функцию Сначала найдём асимптоту
Таким образом, при Теперь найдём асимптоту при
Поскольку
Вычисление
Рис.7.13.График
Замечание 7.3 Если график
то Однако асимптота может существовать и в случае, когда производная
33)
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 327; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.44.232 (0.009 с.) |






 равна
равна  откуда следует, что квадратичная функция выпукла вниз на всей области определения.
откуда следует, что квадратичная функция выпукла вниз на всей области определения. и имеет в этой точке конечную или бесконечную производную. Тогда точка
и имеет в этой точке конечную или бесконечную производную. Тогда точка 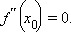
 Если
Если  меняет знак при переходе через точку
меняет знак при переходе через точку  то
то 
 то
то 
 );
);

 у функции
у функции 

 называется вертикальная прямая
называется вертикальная прямая 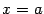 , если
, если  или
или  при каком-либо из условий:
при каком-либо из условий:  ,
,  ,
,  . Заметим, что мы при этом не требуем, чтобы точка
. Заметим, что мы при этом не требуем, чтобы точка 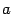 принадлежала области определения функции
принадлежала области определения функции  , однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки:
, однако она должна быть определена по крайней мере в какой-либо из односторонних окрестностей этой точки: 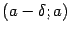 или
или  , где
, где  .
. . График
. График  , поскольку при
, поскольку при  выполняется условие
выполняется условие  , а также при
, а также при  выполняется условие
выполняется условие  .
.
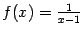
 . Её график имеет вертикальную асимптоту
. Её график имеет вертикальную асимптоту 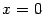 , так как
, так как 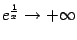 при
при  . То, что при
. То, что при  функция
функция  при
при 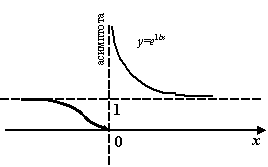
 . Прямая
. Прямая 
 называется прямая
называется прямая  , если выполнены два условия:
, если выполнены два условия:  целиком содержится в
целиком содержится в  ;
; 
 называется прямая
называется прямая  целиком содержится в
целиком содержится в 

 , она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая
, она называется горизонтальной асимптотой. Таким образом, горизонтальная асимптота -- частный случай наклонной асимптоты; прямая  является горизонтальной асимптотой графика
является горизонтальной асимптотой графика 
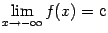
 . График этой функции имеет наклонную асимптоту
. График этой функции имеет наклонную асимптоту 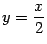 при
при  при
при 
 имеет горизонтальную асимптоту
имеет горизонтальную асимптоту  как при
как при  при
при  . Можно сказать также, что асимптота при
. Можно сказать также, что асимптота при 
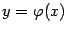 называется асимптотической линией графика функции
называется асимптотической линией графика функции  -- линейная, то есть график
-- линейная, то есть график  . Так как
. Так как  при
при  как асимптотическую линию при
как асимптотическую линию при 
 и
и  не очевидны, можно применять следующую теорему.
не очевидны, можно применять следующую теорему.
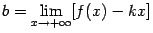
 и
и 


 и
и  , так что
, так что

 .
.

 и
и  , так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение
, так что обе наклонные асимптоты совпадают друг с другом и имеют уравнение  , то есть, фактически, асимптота только одна.
, то есть, фактически, асимптота только одна.
 . При
. При  , а при
, а при  .
.
 . Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.
. Покажем, что обе её наклонные асимптоты существуют, но не совпадают друг с другом.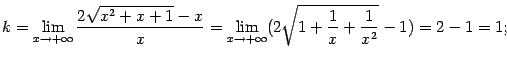
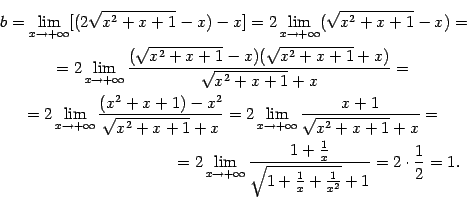
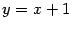 .
.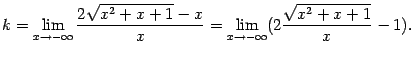
 . В полученной дроби поделим числитель и знаменатель на положительное число
. В полученной дроби поделим числитель и знаменатель на положительное число 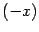 . Тогда под корнем нужно будет поделить на
. Тогда под корнем нужно будет поделить на 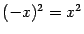 , и получится:
, и получится:
 , так что наклонная асимптота при
, так что наклонная асимптота при 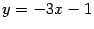 .
.
 и его две наклонных асимптоты
и его две наклонных асимптоты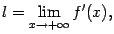
 . Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты17.
. Иными словами, если угловой коэффициент касательной имеет предел, то этот предел равен угловому коэффициенту асимптоты17. не имеет никакого предела при
не имеет никакого предела при 


