
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифференцируемость функций. Непрерывность дифференцируемой функцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Функция y=f(x) называется дифференцируемой в некоторой точке x 0, если она имеет в этой точке определенную производную, т.е. если предел отношения Если функция дифференцируема в каждой точке некоторого отрезка [ а; b ] или интервала (а; b), то говорят, что она дифференцируема на отрезке [ а; b ] или соответственно в интервале (а; b). Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями. Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0, то она в этой точке непрерывна. Таким образом,из дифференцируемости функции следует ее непрерывность. Доказательство. Если
где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δ x →0. Но тогда Δ y = f '(x 0) Δ x +αΔ x => Δ y →0 при Δ x →0, т.е f(x) – f(x 0) →0 при x → x 0, а это и означает, что функция f(x) непрерывна в точке x 0. Что и требовалось доказать. Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).
В точке a при Δ x →0 отношение В точке b при Δ x →0 отношение В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.
1. Рассмотрим функцию y=|x|. Эта функция непрерывна в точке x = 0, т.к. Покажем, что она не имеет производной в этой точке. f (0+Δ x) = f (Δ x) = |Δ x |. Следовательно, Δ y = f (Δ x) – f (0) = |Δ x | Но тогда при Δ x < 0 (т.е. при Δ x стремящемся к 0 слева) А при Δ x > 0
Т.о., отношение 2. Функция
Следовательно, рассматриваемая функция не дифференцируема в точке x = 0. Касательная к кривой в этой точке образует с осью абсцисс угол p/2, т.е. совпадает с осью Oy.
19)
20) Частные производные первого порядка и их геометрическое истолкование Пусть задана функция z = ƒ (х; у). Так как х и у — независимые переменные, то одна из них может изменяться, а другая сохранять свое значение. Дадим независимой переменной х приращение Δх, сохраняя значение у неизменным. Тогда z получит приращение, которое называется частным приращением z по х и обозначается ∆хz. Итак, Δхz=ƒ(х+Δх;у)-ƒ(х;у). Аналогично получаем частное приращение z по у:Δуz=ƒ(x;у+Δу)-ƒ(х;у). Полное приращение Δz функции z определяется равенством Δz = ƒ(х + Δх;у + Δу)- ƒ(х; у). Если существует предел
то он называется частной производной функции z = ƒ (х; у) в точке М(х;у) по переменной х и обозначается одним из символов:
Частные производные по х в точке М0(х0;у0) обычно обозначают символами Аналогичноопределяется и обозначается частная производная от z=ƒ(х;у) по переменной у:
Таким образом, частная производная функции нескольких (двух, трех и больше) переменных определяется как производная функции одной из этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции ƒ(х;у) находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно х или у считается постоянной величиной). Пример 44.1. Найти частные производные функции z = 2у + ех2-у +1. Решение:
Частные производные высших порядков Частные производные
Аналогично определяются частные производные 3-го, 4-го и т. д. порядков. Так, Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Таковыми являются, например,
21)
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 658; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

 существует и конечен.
существует и конечен. , то
, то ,
, Рассмотрим на рисунке точки а, b, c.
Рассмотрим на рисунке точки а, b, c. . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.
. Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной. Примеры.
Примеры. .
.

 определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x = 0.
определена и непрерывна на всей числовой прямой. Выясним, имеет ли эта функция производную при x = 0.





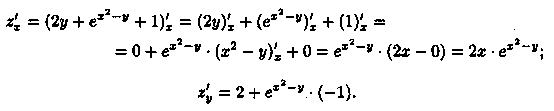
 называют частными производными первого порядка. Их можно рассматривать как функции от (х;у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
называют частными производными первого порядка. Их можно рассматривать как функции от (х;у) є D. Эти функции могут иметь частные производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
 и т.д.
и т.д.



