
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Окрестностное определение по КошиСодержание книги Поиск на нашем сайте Значение
Геометрическая интерпретация предела функции. Обратимся к рисунку 1, на котором представлен фрагмент графика функции
Предельным положением секущей AB при перемещении точки B к точке A по дуге кривой
11)
12) Первым замечательным пределом именуют
Все приведенные выше формулы получаются из основной:
Осуществим следующее преобразование: в числителе домножим на 7х и разделим на 7х. этим мы не изменяем значение числителя. Аналогичную операцию проделаем в знаменателе:
Что нам это даст? Так как при
Сокращая х и вспомнив, что
13) Классификация бесконечно малых функций Во многих случаях представляет интерес сравнение бесконечно малых между собой по характеру их приближения к нулю. Рассмотрим две бесконечно малые a(x) и b(x) при x®x0 и предположим, что b(x) не обращается в ноль в некоторой проколотой окрестности точки x0. Будем сравнивать эти бесконечно малые, изучая поведение их отношения при x®x0. Дадим следующие определения. Если Если Если a(x) и bk(x) – бесконечно малые одного порядка (k>0), то говорят, что b(x) величина k-го порядка относительно бесконечно малой a(x) при x®x0 и пишут Если Замечание. Та же терминология применяется и при сравнении функций, не являющихся бесконечно малыми при x®x0. В этом случае добавляется ещё одно определение. Если существует число C > 0 такое, что в некоторой проколотой окрестности точки x0 справедливо неравенство Примеры. 1. Привести примеры на каждое из определений. 2. Доказать, что 3. Вычислить: 4. Доказать, что Логарифм по основанию e (e - трансцендентное число, приближенно равное 2,718281828...) называется натуральным логарифмом. Натуральный логарифм числа x обозначается ln x. Натуральные логарифмы широко используются в математике, физике и инженерных расчетах.
14) Непрерывная функция — функция без «скачков», то есть такая у которой малые изменения аргумента приводят к малым изменениям значения отображения. График непрерывной функции можно начертить «не отрывая карандаш от бумаги». Непрерывная функция вообще говоря, — синоним понятия непрерывное отображение, тем не менее, чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающих вещественные значения. Точки разрыва Если попытаться построить отрицание свойства непрерывности функции в точке (предельной для области определения), то получится следующее. Существует такая окрестность значения функции в рассматриваемой точке, что сколь близко мы не подходили бы к данной точке, всегда можно будет найти точку, значение в которой окажется за пределами заданной окрестности. В этом случае говорят, что функция f терпит разрыв в точке a.
Возможны два варианта: § либо предел функции существует, но он не совпадает со значением функции в данной точке:
тогда точка a называется точкой устранимого разрыва функции f (в комплексном анализе — устранимая особая точка). Положив § либо предела функции в данной точке не существует. В этом случае для числовой функции, заданной на вещественной прямой (или её подмножестве), возможно существование односторонних пределов. Отсюда возникает классификация точек (неустранимого) разрыва: § если оба односторонних предела существуют и конечны, но хотя бы один из них отличен от значения функции в данной точке, то такую точку называют точкой разрыва первого рода; § если хотя бы один из односторонних пределов не существует или не является конечной величиной, то такую точку называют точкой разрыва второго рода. Точка, в которой функция не определена, будет точкой разрыва функции лишь при условии, если функция определена, хотя бы с одной стороны вблизи этой точки.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 452; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 называется пределом (предельным значением) функции
называется пределом (предельным значением) функции 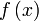 в точке
в точке  , если для любой окрестности
, если для любой окрестности  точки
точки 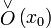 точки
точки 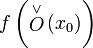 лежит в
лежит в 
 .
.
 на промежутке [ x, x + ∆ x ]:
на промежутке [ x, x + ∆ x ]:


 в точке x равна тангенсу угла, образованного касательной к графику функции
в точке x равна тангенсу угла, образованного касательной к графику функции  . Тогда число A называют правосторонним пределом (или пределом справа) функции
. Тогда число A называют правосторонним пределом (или пределом справа) функции  и обозначают любым из символических выражений
и обозначают любым из символических выражений
 Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае
Понятие левостороннего предела (или предела слева) вводится аналогичным образом. В этом случае  при x → a со стороны меньших значений:
при x → a со стороны меньших значений:
 Для существования обычного (двустороннего) предела функции
Для существования обычного (двустороннего) предела функции 
 Например, в точке x = 3 односторонние пределы функции
Например, в точке x = 3 односторонние пределы функции
 отличаются друг от друга:
отличаются друг от друга:
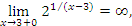
 Поэтому в рассматриваемой точке предел функции
Поэтому в рассматриваемой точке предел функции  . Известны также и следствия из первого замечательного предела:
. Известны также и следствия из первого замечательного предела:
 , то
, то 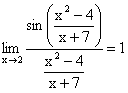 . Собственно говоря, на этом и основаны примеры на первый замечательный предел. Суть решения таких заданий проста: формально подогнать условие под вид первого замечательного предела, после чего использовать формулу
. Собственно говоря, на этом и основаны примеры на первый замечательный предел. Суть решения таких заданий проста: формально подогнать условие под вид первого замечательного предела, после чего использовать формулу  . Простой подстановкой
. Простой подстановкой 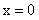 проблему не решить, потому как
проблему не решить, потому как  , т.е. тут мы имеем дело с неопределенностью вида
, т.е. тут мы имеем дело с неопределенностью вида 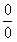 . Если такая неопределенность встречается вкупе с тригонометрическими выражениями, то для стандартных типовых расчетов это почти стопроцентная гарантия первого замечательного предела. Подгоним данную задачу под вид упомянутого предела, учитывая
. Если такая неопределенность встречается вкупе с тригонометрическими выражениями, то для стандартных типовых расчетов это почти стопроцентная гарантия первого замечательного предела. Подгоним данную задачу под вид упомянутого предела, учитывая 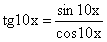 :
:

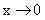 имеем
имеем 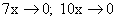 , то можно применить первый замечательный предел:
, то можно применить первый замечательный предел:  . Учитывая это, получим:
. Учитывая это, получим: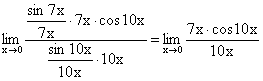
 , получим:
, получим:  . Приведем ещё несколько примеров решения задач на первый замечательный предел:
. Приведем ещё несколько примеров решения задач на первый замечательный предел: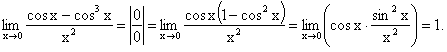




 , то говорят, что a(x) и b(x) бесконечно малые одного порядка при x®x0.
, то говорят, что a(x) и b(x) бесконечно малые одного порядка при x®x0. , то говорят, что a(x) бесконечно малая более высокого порядка по сравнению с b(x) при x®x0, и пишут
, то говорят, что a(x) бесконечно малая более высокого порядка по сравнению с b(x) при x®x0, и пишут 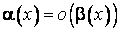 , x®x0.
, x®x0. , x®x0.
, x®x0. , то говорят, что a(x) и b(x) эквивалентные бесконечно малые при x®x0 и пишут
, то говорят, что a(x) и b(x) эквивалентные бесконечно малые при x®x0 и пишут  , x®x0.
, x®x0.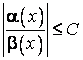 , то говорят, что функция a(x) ограничена относительно функции b(x) при x®x0, и пишут
, то говорят, что функция a(x) ограничена относительно функции b(x) при x®x0, и пишут  , x®x0.
, x®x0. при x®0.
при x®0. .
. при x®0.
при x®0.

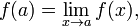 можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.
можно добиться непрерывности функции в этой точке. Такое изменение значения функции в точке, превращающее функцию в непрерывную в этой точке, называется доопределением по непрерывности.


