
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрический и механический смысл производнойСодержание книги
Поиск на нашем сайте
Геометрический смысл производной Пусть функция
Рис. 2 Придав произвольное приращение аргументу Касательной к графику функции Для того, чтобы секущая Угловой коэффициент касательной получается путем перехода от
Таким образом, получим, что
В случае бесконечной производной Из уравнения секущей имеем:
Переходя в равенстве к пределу при Механический смысл производной Пусть материальная точка движется прямолинейно и Для определения скорости Отношение
Предел Таким образом, мгновенная скорость в момент времени Примеры задач Задача 1. Составьте уравнение общей касательной к графикам функций Решение. I способ. Прямая
Прямые совпадают, если их угловые коэффициенты и свободные члены равны. Отсюда
Решением системы будут
УРАВНЕНИЯ КАСАТЕЛЬНОЙ И НОРМАЛИ К КРИВОЙ Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку M (x0, y0), и составим уравнение касательной к данной кривой в точке M, предполагая, что эта касательная не параллельна оси Oy. Уравнение прямой с угловым коэффициентом в общем виде есть у=kx+b. Поскольку для касательной k = f '(x0), то получаем уравнение y = f '(x0)· x + b. Параметр b найдем из условия, что касательная проходит через точку M(x0, y0). Поэтому ее координаты должны удовлетворять уравнению касательной: y0 = f ' (x0) · x0 + b. Отсюда b = y0 – f '(x0)· x0. Таким образом, получаем уравнение касательной y = f '(x0)· x + y0 – f '(x0)· x0 или
Если касательная, проходящая через точку М (x0, y0) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение x= x0. Наряду с касательной к кривой в данной точке часто приходится рассматривать нормаль. Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.
Учитывая, что нормаль также как и касательная проходит через точку M (x 0, y 0 ), то уравнение нормали к кривой y= f(x) в данной точке M имеет вид:
Ясно, что если касательная параллельна оси Ox, т.е. f '(x 0) = 0 и ее уравнение имеет вид y= y 0, то нормаль в этой же точке будет перпендикулярна оси Ox. Значит, ее уравнение имеет вид x= x 0. Примеры. 1. Составить уравнения касательной и нормали к графику функции у = tg 2 x в точке с абсциссой x 0 =π/4.
Уравнение касательной имеет вид y =4·(x – π/4) + 1 или y = 4 x – π + 1. Уравнение нормали будет y = –1/4·(x – π/4) + 1 или у = –1/4· x + π/16 + 1. 2. Составить уравнения касательной и нормали к графику функции у = 0.5·(x – 2) 2 + 5 в точке M (2; 5). y '= x – 2, y '(2) = 0. Следовательно, касательная параллельна оси Ox, а значит ее уравнение y = 5. Тогда нормаль параллельна оси Oy и имеет уравнение x = 2. 3. Найти уравнение касательной и нормали к эллипсу Найдем y ' по правилу дифференцирования неявной функции Уравнение касательной: Уравнение нормали: 4. Составить уравнения касательной и нормали к циклоиде x = t – sin t, y = 1 – cos t в точке М (x 0; y 0), которая соответствует значению параметра t = π/2. При t =π/2 x 0 = π/2 – 1, y 0 =1.
Уравнение касательной: y = x – π/2 + 1 + 1, т.е. у = x – π/2 + 2. Уравнение нормали: y = – x – π/2 – 1 + 1, т.е. у = – x – π/2.
Правила дифференцирования Если функции f и g дифференцируемы в точке
Доказательство а) Постоянный множитель C можно выносить из-под знака производной: В частности, б) Функцию f · g можно записать в виде в) Для доказательства этой формулы заметим, что Если f дифференцируема, то Доказательство этой формулы предоставляем читателю. Если функция y = f (x) непрерывна и строго возрастает в окрестности точки Если функции y = f (x) и z = g (y) дифференцируемы в точках x 0 и y 0 = f (x 0) соответственно, то сложная функция z = g (f (x)) дифференцируема в точкеx 0, причем Следствием этой теоремы является тот факт, что дифференциал функции y = f (x) имеет один и тот же вид Если f (x) – четная функция, то Пусть в окрестности точки t 0 определены функции x (t) и y (t), причем x (t) непрерывна и строго монотонна. Пусть в этой окрестности существуют производные 18) Понятие дифференциала и его геометрический смысл Пусть функция
Таким образом, приращение функции 1) 2) Определение. Дифференциалом функции называется главная, линейная относительно
Пример. Найти приращение функции Решение. Пример. Найти дифференциал функции Решение. По формуле (7.2.) имеем
Тогда формулу (7.2) для дифференциала функции можно записать в виде:
Откуда
Следовательно, с геометрической точки зрения дифференциал функции есть приращение ординаты касательной, проведенной к графику функции
|
|||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 268; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.007 с.) |

 определена в некоторой окрестности
определена в некоторой окрестности  токи
токи  , непрерывна в этой точке и
, непрерывна в этой точке и  , а
, а  (рис.2).
(рис.2).
 , так чтобы
, так чтобы  , перейдем к точке
, перейдем к точке  с абсциссой
с абсциссой  и ординатой
и ординатой  , где
, где  Уравнение прямой, проходящей через точки
Уравнение прямой, проходящей через точки  и
и  , имеет вид:
, имеет вид:  , где отношение
, где отношение 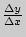 представляет собой угловой коэффициент секущей (
представляет собой угловой коэффициент секущей ( .
. , при стремлении точки
, при стремлении точки  стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел
стремилась к предельному положению, отличному от вертикальной прямой, необходимо и достаточно, чтобы существовал конечный предел  , то есть, чтобы существовала конечная производная функции
, то есть, чтобы существовала конечная производная функции  в точке
в точке 
 , где
, где  - угол наклона касательной к оси
- угол наклона касательной к оси  (см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции
(см. рис.), а значение производной равно угловому коэффициенту касательной к графику функции. В этом заключается геометрический смысл производной. Уравнение касательной к графику функции 
 .
.
 , то есть касательная является в данном случае вертикальной прямой, проходящей через точку
, то есть касательная является в данном случае вертикальной прямой, проходящей через точку  - длина пути, проходимого за время
- длина пути, проходимого за время 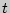 , отсчитываемого от некоторого момента времени
, отсчитываемого от некоторого момента времени  .
. в данный момент
в данный момент  , при этом приращение пути будет равно
, при этом приращение пути будет равно  .
. называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени
называется в физике величиной средней скорости движения за промежуток времени, начиная с момента времени 
 называется величиной мгновенной скорости движения в момент времени
называется величиной мгновенной скорости движения в момент времени 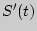 .
. и
и  .
. является общей касательной графиков функций
является общей касательной графиков функций  и
и  , если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке.
, если она касается как одного, так и другого графиков, но совершенно не обязательно в одной и той же точке. - уравнение касательной к графику функции y=x2 в точке с абсциссой x0
- уравнение касательной к графику функции y=x2 в точке с абсциссой x0 - уравнение касательной к графику функции y=x3 в точке с абсциссой x1
- уравнение касательной к графику функции y=x3 в точке с абсциссой x1


 Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством:
Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом касательной k равенством: .
.
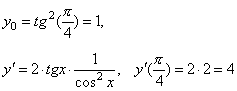
 в точке M (2; 3).
в точке M (2; 3). .
. ,т.е.
,т.е.  .
. , т.е.
, т.е.  .
. .
. то в этой же точке дифференцируемы сумма, произведение и частное (если
то в этой же точке дифференцируемы сумма, произведение и частное (если  ) этих функций, причем
) этих функций, причем


 По свойству предела суммы получаем
По свойству предела суммы получаем 


 Но
Но  По свойству предела произведения получаем
По свойству предела произведения получаем  Используя доказанное равенство, получим, что
Используя доказанное равенство, получим, что  Раскрывая скобки и приводя подобные члены, получим формулу
Раскрывая скобки и приводя подобные члены, получим формулу 
 Воспользовавшись свойством предела частного, получим
Воспользовавшись свойством предела частного, получим  После этого представим
После этого представим  как произведение функций f и
как произведение функций f и  откуда и следует доказываемая формула.
откуда и следует доказываемая формула. где
где  также дифференцируема, причем
также дифференцируема, причем 
 то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем
то функция x = φ (y), обратная к функции y = f (x), дифференцируема в точке y 0 = f (x 0), причем 

 как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного.
как в случае, когда x – независимая переменная, так и в случае, когда x – дифференцируемая функция другого переменного. – нечетная; если f (x) – нечетная функция, то
– нечетная; если f (x) – нечетная функция, то  и
и  Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем
Тогда сложная функция y = y (t (x)), где t (x) – функция, обратная x (t), дифференцируема по x, причем 
 определена на промежутке
определена на промежутке  и дифференцируема в окрестности точки
и дифференцируема в окрестности точки  ,тогда
,тогда  или по теореме о связи бесконечно малых с пределами функций имеем
или по теореме о связи бесконечно малых с пределами функций имеем  , где
, где  - бесконечно малая величина при
- бесконечно малая величина при  . Отсюда:
. Отсюда: .
. состоит из двух слагаемых:
состоит из двух слагаемых: - линейного относительно
- линейного относительно  , т.к.
, т.к.  ;
; - нелинейного относительно
- нелинейного относительно  .
. .
. при
при  и
и  :
:
 ,
, 
 .
. . Определение. Дифференциал независимой переменной
. Определение. Дифференциал независимой переменной  равен приращению этой переменной:
равен приращению этой переменной:

 , поэтому
, поэтому 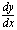 можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем
можно рассматривать не только как символическое обозначение производной, но и как обычную дробь с числителем  и знаменателем
и знаменателем  .
.
 (рис. 7.1.) возьмем произвольную точку
(рис. 7.1.) возьмем произвольную точку  . Дадим аргументу
. Дадим аргументу  , тогда функция получает приращение
, тогда функция получает приращение  . В точке
. В точке  проведем касательную, образующую угол
проведем касательную, образующую угол 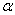 с осью
с осью  . Из треугольника
. Из треугольника  :
:  . Из
. Из  имеем:
имеем:  . Таким образом,
. Таким образом,  и соответствует формуле
и соответствует формуле



