
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о подпоследовательности числовой по-Содержание книги
Поиск на нашем сайте
следовательности Пусть Полученная последовательность называется подпоследо-вательностью последовательности
Теорема Больцано–Вейерштрасса. Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.
Доказательство: Т.к. последовательность
Необходимое и достаточное условие сходимости последовательности. Критерий Коши До сих пор мы с вами выясняли вопрос о сходимости последовательности Хорошо бы иметь такой критерий сходимости последова-тельности, который имеет дело только с самими ее элементами. Такой критерий имеется. Для его формулировки сначала введем понятие фундаментальной последовательности.
Определение. Последовательность
Теорема (критерий Коши; Коши – известный французский математик 19 века). Для того чтобы последовательность Эта теорема дается без доказательства.
Пример.
Применим критерий Коши для установления сходимости следующей последовательности
Учитывая, что
Функция. Предел функции. Непрерывность Функции Определение предела функции
В самом начале нашего курса мы познакомились с определением функции и области ее определения. Одной из наиболее употребимых моделей функций являются непрерывные функции. Для изучения их свойств необходимо ввести понятие предела функции. Рассмотрим функцию
Определение 1. Число b называется пределом функции Это определение дано на привычном языке последовательностей и их пределов. Есть другое определение, не связанное с понятием последовательности.
Определение 2. Число b называется пределом функции x = a, если для любого Записывают так:
Говорят еще так: первое определение предела функции – через предел последовательности, второе – на языке Можно доказать, что каждое из этих определений следует из другого. Таким образом, оба определения эквивалентны и в зависимости от удобства можно использовать и то и другое. Мы познакомились с определением предела в конечной точке x=a. Дадим определение предела при Число b называется пределом M > K, такое что
Записывают так: Аналогичное определение можно дать для предела при
Определение. Функция Функция
Рассмотрим примеры.
Пример 1. Докажем, что
Замечание. Для существования предела при
Пример 2. Доказать, что Функция
Пример 3. Докажем, что
Итак, если
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 676; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.45.82 (0.009 с.) |

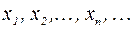 – некоторая последовательность. Рассмотрим произвольную бесконечную возрастающую последовательность целых положительных чисел
– некоторая последовательность. Рассмотрим произвольную бесконечную возрастающую последовательность целых положительных чисел  . Выберем из последовательности
. Выберем из последовательности  элементы с номерами
элементы с номерами 
 .
. . Поделим пополам отрезок [ a, b ] и в качестве
. Поделим пополам отрезок [ a, b ] и в качестве  возьмем ту его половину, к которой принадлежит бесконечное число элементов
возьмем ту его половину, к которой принадлежит бесконечное число элементов  . Снова поделим
. Снова поделим  , содержащее бесконечное число элементов
, содержащее бесконечное число элементов  с номером
с номером 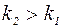 (это всегда можно сделать, т. к. в
(это всегда можно сделать, т. к. в  , таких, что каждый последующий принадлежит предыдущему, а
, таких, что каждый последующий принадлежит предыдущему, а 
 Тогда по принципу вложенных отрезков существует точка
Тогда по принципу вложенных отрезков существует точка  для всех k. Очевидно, выбранная таким образом подпоследовательность
для всех k. Очевидно, выбранная таким образом подпоследовательность  имеет своим пределом C.
имеет своим пределом C.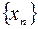 в соответствии с определением предела, т.е. нам приходилось оценивать разность элементов
в соответствии с определением предела, т.е. нам приходилось оценивать разность элементов 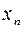 этой последовательности и ее предполагаемого предела a. Иными словами, приходилось предугадывать, чему равен предел а.
этой последовательности и ее предполагаемого предела a. Иными словами, приходилось предугадывать, чему равен предел а.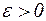 найдется номер
найдется номер 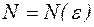 такой, что для всех
такой, что для всех  справедливо неравенство
справедливо неравенство  .
. , где
, где 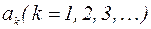 – произвольные вещественные числа, удовлетворяющие условию
– произвольные вещественные числа, удовлетворяющие условию  Пусть m и n – любые два натуральных числа. Пусть для определенности m > n. Тогда
Пусть m и n – любые два натуральных числа. Пусть для определенности m > n. Тогда
 , для любого
, для любого  Тогда при
Тогда при 
 , т.е. последователь-ность
, т.е. последователь-ность  , определенную на множестве
, определенную на множестве  и точку а, быть может и не принадлежащую множеству
и точку а, быть может и не принадлежащую множеству  имеются точки множества
имеются точки множества 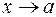 ), если для любой сходящейся к а последовательности
), если для любой сходящейся к а последовательности 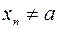 ), соответствующая последовательность
), соответствующая последовательность  значений функции сходится к b.
значений функции сходится к b. можно указать
можно указать  такое, что для всех x, для которых
такое, что для всех x, для которых  , выполняется неравенство
, выполняется неравенство  .
. или
или 

 .
. , если
, если 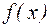 определена для всех x, удовлетворяющих неравенству x > K при некотором K > 0 и для любого
определена для всех x, удовлетворяющих неравенству x > K при некотором K > 0 и для любого 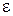 >0 можно найти число
>0 можно найти число .
. В дальнейшем в записи
В дальнейшем в записи  величину а будем считать как конечной, так и бесконечной
величину а будем считать как конечной, так и бесконечной  Более того, и значение предела b может быть либо конечным, либо бесконечным
Более того, и значение предела b может быть либо конечным, либо бесконечным  , называется бесконечно малой при
, называется бесконечно малой при  , называется бесконечно большой при
, называется бесконечно большой при 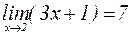 . Пусть задано произвольное число
. Пусть задано произвольное число  , необходимо выполнение следующих неравенств:
, необходимо выполнение следующих неравенств:  Обозначим
Обозначим  . Тогда, если
. Тогда, если  то
то  , а это и означает, что
, а это и означает, что 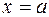 . При нахождении предела рассматриваются значения функции в окрестности точки a, а не в самой точке a. Это положение наглядно иллюстрируется следующим примером.
. При нахождении предела рассматриваются значения функции в окрестности точки a, а не в самой точке a. Это положение наглядно иллюстрируется следующим примером. .
. не определена при
не определена при  Надо доказать, что при произвольном
Надо доказать, что при произвольном  , что будет выполняться неравенство
, что будет выполняться неравенство  , если
, если  . Но при
. Но при 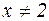 неравенство (*) эквивалентно неравенству
неравенство (*) эквивалентно неравенству  , т.е.
, т.е.  . Таким образом, если положить
. Таким образом, если положить 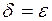 , то при
, то при  , а это означает, что при
, а это означает, что при  функция
функция  .
. или
или  Надо доказать, что
Надо доказать, что  , если
, если  , причем N определяется выбором
, причем N определяется выбором 

 то
то  при
при 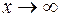 .
.


