
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные правила и формулы дифференцированияСодержание книги
Поиск на нашем сайте
Дифференцированием мы будем называть вычисление производной. Если функции
Доказательство. 1) Дадим приращение аргументу 2) 3) 4) Частный случай.
(Постоянный сомножитель можно выносить за знак производной).
Производные некоторых основных элементарных функ- ций 1.
2. Т.е. мы можем воспользоваться формулой
Оказывается, формула
3.
Доказательство.
4.
5.
6.
7.
7а.
8. Доказательство.
Дифференциал функции
Если функция f имеет в точке х производную, то существует предел Отсюда: Тогда
Если обозначить Говорят, что функция f дифференцируема в точке х, если ее приращение в этой точке Если функция f имеет в точке х производную, она называется дифференцируемой в этой точке (т.е. Если функция f дифференцируема в точке х, то она имеет производную Таким образом, понятия дифференцируемости и наличия производной отождествляются. Если в (2) Этот главный член приращения называют дифференциалом функции Таким образом, производная от f в точке х равна
Пример. Пример использования дифференциала для приближен-ных вычислений. Нужно прикинуть, сколько (какой объем) материала истрачено на изготовление кубической коробки с внутренним размером ребра коробки 10см и толщиной стенок 1мм. Объем куба Объем стенок коробки
Точное значение Точность приближенного вычисления
Производная сложной функции, обратной функции, функции, заданной параметрически
Пусть задана сложная функция
Доказательство. Т.к. функция f имеет производную, то она дифференцируема, т.е. Разделим на
Или
Пример. Найти производную функции
Практически дифференцируют, не вводя промежуточных аргументов.
Производная обратной функции
Теорема. Если
Доказательство.
Примеры использования производной от обратной функции 1. Найти Теперь: если
Если а=е, т.е. у=lnx, то
Производные обратных тригонометрических функций
Обратная функция x=siny имеет производную Поэтому
Аналогично Таким образом, у нас имеется таблица производных основных элементарных функций. Тем самым ясно, как вычислять производные элементарных функций, которые получают из основных элементарных путем конечного числа арифметических операций и взятия функции от функции.
Производная функции, заданной параметрически Пусть х и у заданы как функции некоторого параметра t:
Каждому значению t соответствуют значения х и у.
Если рассматривать эти значения x и y как координаты точки на плоскости xОy, то каждому значению t соответствует определенная точка плоскости. При изменении t от Уравнения (1) называются параметрическими уравне-ниями этой кривой, t называется параметром, а способ задания кривой (1) –параметрическим. Предположим, что функция По правилу дифференцирования сложной функции
Эта формула называется формулой дифференцирования функции, заданной параметрически. Пример:
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 625; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.69.138 (0.009 с.) |

 и
и  имеют производные в точке х, то их сумма, разность, произведение и частное(при условии, что
имеют производные в точке х, то их сумма, разность, произведение и частное(при условии, что  ) имеют производные и справедливы равенства:
) имеют производные и справедливы равенства: ; (1)
; (1) ; (2)
; (2)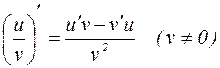 . (3)
. (3) , а соответствующие приращения функций u и v обозначим
, а соответствующие приращения функций u и v обозначим 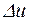 и
и  . Тогда
. Тогда




 . Докажем при
. Докажем при 







 для n – отрицательных:
для n – отрицательных: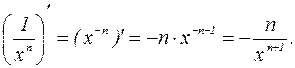
 .
.

 . Доказать самостоятельно.
. Доказать самостоятельно.

 Доказательство аналогичное.
Доказательство аналогичное.









 . (1)
. (1) , то
, то  . (2)
. (2) можно записать в виде (2), где
можно записать в виде (2), где 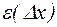 – бесконечно малая функция
– бесконечно малая функция  (
( ).
).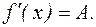
 , то
, то  называется главным линейным членом приращения – он пропорционален
называется главным линейным членом приращения – он пропорционален  . Приближенно, пренебрегая при малых
. Приближенно, пренебрегая при малых  .
. :
:  .
.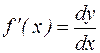 , т.е. она равна отношению дифференциала функции f к соответствующему дифференциалу независимой переменной х. При этом
, т.е. она равна отношению дифференциала функции f к соответствующему дифференциалу независимой переменной х. При этом  не зависит от х, а
не зависит от х, а  зависит как от х, так и от
зависит как от х, так и от  .
. , где х – длина его ребра.
, где х – длина его ребра.

 .
.


 При этом функция
При этом функция  имеет производную в точке х, а функция f имеет производную в точке
имеет производную в точке х, а функция f имеет производную в точке  . Тогда существует производная от F в точке х, равная
. Тогда существует производная от F в точке х, равная 
 , при этом
, при этом 
 и перейдем к пределу при
и перейдем к пределу при  x
x 

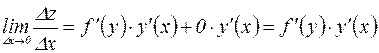

 ;
; ,
,  ,
,  ,
,  .
.

 – строго монотонная непрерывная функция и
– строго монотонная непрерывная функция и  – обратная к ней функция, имеющая в точке у производную
– обратная к ней функция, имеющая в точке у производную  , то функция f имеет в соответст-вующей точке х производную
, то функция f имеет в соответст-вующей точке х производную .
. , так как функция f(x) непрерывна, то при
, так как функция f(x) непрерывна, то при и
и  , тогда
, тогда  .
. . Мы уже вывели эту формулу. Вывод был достаточно громоздкий.
. Мы уже вывели эту формулу. Вывод был достаточно громоздкий. , то
, то  ,
,  .
. – результат тот же самый.
– результат тот же самый. .
. – строго возрастает на отрезке [- 1,1 ]. Напомню график
– строго возрастает на отрезке [- 1,1 ]. Напомню график
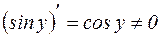 , если
, если  .
.


 . (1)
. (1)
 эта точка описывает на плоскости некоторую кривую.
эта точка описывает на плоскости некоторую кривую.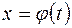 имеет обратную,
имеет обратную,  , тогда
, тогда  т.е. у является сложной функцией от х.
т.е. у является сложной функцией от х. . Но по правилу дифференцирования обратной функции
. Но по правилу дифференцирования обратной функции  .
.




