
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Тейлора для функции двух переменныхСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формула Тейлора для функции одной переменной
Здесь
Формула Тейлора позволяет вычислить функцию Аналогичная формула имеет место для функции двух переменных и вообще для функции многих переменных. В частности, если
Здесь Выпишем эти дифференциалы при
где
Упражнение. Выписать самостоятельно полный дифференциал третьего порядка функции двух переменных. Замечание. Если
Пример 1. Разложить функцию Сначала найдем частные производные:
Все остальные производные равны нулю, так что формула Тейлора имеет ограниченное число членов. Найдем функцию и ее частные производные в точке
вторые частные производные равны константам, которые мы уже вычислили. Таким образом,
Пример 2. Используя формулу Тейлора до членов второго порядка включительно, вычислить приближенно значение
Пусть Тогда
Таким образом,
Экстремум функции двух переменных
Определение 1. Функция z=f(x,y) имеет максимум в точке M0(x0,y0), если f(x0,y0)>f(x,y) для всех точек (х,у), достаточно близких к точке (х0,у0) и отличных от нее. Определение 2. Функция z=f(x,y) имеет минимум в точке M0(x0,y0), если f(x0,y0)<f(x,y) для всех точек (х,у), достаточно близких к точке (х0,у0) и отличных от нее. Как обычно, точки максимума и минимума называют точками экстремума. Пример. Рассмотрим функцию z=(x–a)2+(y–b)2+1. Очевидно, при х=а и у=b, z=1. Но если х¹а, у¹b, то (x–a)2+(y–b)2>0, поэтому в любой точке, отличной от М(а,b), z>1. Следовательно, в точке М(а,b) функция имеет минимум, т.к. z(a,b)<z(x,y).
Можно дать немного другие определения. Пусть
Df = f(x, y) – f(x0, y0) = f(x0 + Dx, y0 + Dy) – f(x0, y0). Определение. Если Df>0 (Df<0) при всех достаточно малых приращениях независимых переменных, то функция f(x,y) достигает в точке М(х0,у0) минимума (максимума). Все приведенные формулировки переносятся на функции любого числа переменных.
Теорема 1 (необходимое условие экстремума). Если функция z=f(x,y) достигает экстремума при х=х0, у=у0, то каждая частная производная первого порядка от z или обращается в ноль, или не существует при х=х0, у=у0. Доказательство очевидно, привести его самостоятельно. Замечание. Условия Пример. z=x2–y2.
В точке х0=0, у0=0 обе частные производные равны нулю, но ни максимума, ни минимума нет (см. рис.).
Теорема 2 (достаточное условие экстремума). Пусть в некоторой области, содержащей точку М0(х0,у0) функция f(x,y) имеет непрерывные частные производные до третьего порядка включительно; пусть, кроме того, точка М0(х0,у0) является критической точкой, т.е.
Тогда при х=х0, у=у0: 1) f(x,y) имеет максимум, если
и
2) f(x,y) имеет минимум, если
и
3) f(x,y) не имеет ни максимума, ни минимума, если
4) если же Теорема 2 дается без доказательства.
Пример. Исследовать на максимум и минимум функцию z=x3+y3–3xy. Сначала находим критические точки:
Решим уравнение x4=x:
x4–x=0, x(x3–1)=0, x(x–1)(x2+x+1)=0, x1=0, x2=1.
Тогда у1=0, у2=1. Таким образом, мы нашли две критические точки: (0;0) и (1;1). Найдем производные второго порядка:
Исследуем характер точки (0;0):
ac – b2 = 0 × 0 – 9 = –9 < 0.
В этой точке экстремума нет. Исследуем характер второй точки (1;1):
ac – b2 = 6 × 6 – 9 = 27 > 0; a > 0.
В точке (1;1) функция имеет минимум, zmin=z(1;1)=–1.
|
|||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 3064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.65.133 (0.009 с.) |

 выглядит следующим образом:
выглядит следующим образом: .
.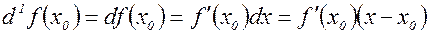 – дифференциал первого порядка;
– дифференциал первого порядка;
 – дифференциал второго порядка;
– дифференциал второго порядка;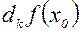 – дифференциал
– дифференциал  -го порядка;
-го порядка; – остаточный член.
– остаточный член. в окрестности точки
в окрестности точки  , если в этой точке известны функция и ее
, если в этой точке известны функция и ее  производных.
производных. – функция двух переменных, непрерывная вместе со своими
– функция двух переменных, непрерывная вместе со своими  и
и  в некоторой области, содержащей точки
в некоторой области, содержащей точки  и
и 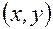 , то имеет место следующая формула Тейлора:
, то имеет место следующая формула Тейлора: .
. – полный дифференциал
– полный дифференциал  и
и  .
. ,
, . Таким образом,
. Таким образом,  – обычный полный дифференциал первого порядка. При
– обычный полный дифференциал первого порядка. При 

 .
. , то формула Тейлора носит название формулы Маклорена.
, то формула Тейлора носит название формулы Маклорена. по формуле Тейлора в окрестности точки
по формуле Тейлора в окрестности точки  .
.
 .
.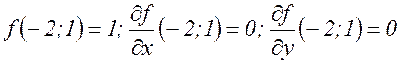 ;
;
 .
. .
. .
.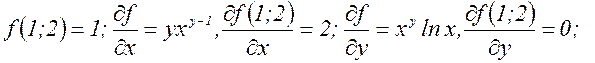

 .
.

 .
. являются необходимыми, но не достаточными. Может оказаться, что оба эти условия выполнены, а экстремума нет.
являются необходимыми, но не достаточными. Может оказаться, что оба эти условия выполнены, а экстремума нет.




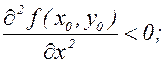



 , то экстремум может быть, а может его и не быть (требуется дополнительное исследование).
, то экстремум может быть, а может его и не быть (требуется дополнительное исследование). .
.



 b=–3;
b=–3; 



