
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 4. Функциональные ряды. Степенные ряды. Формула ТейлораСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
4.1. Функциональные ряды: основные понятия, область сходимости Определение 1. Ряд, члены которого являются функциями одной или Рассмотрим функциональный ряд Определение 2. Областью сходимости функционального ряда Функциональный ряд сходится в области Как находить область сходимости функционального ряда Пример 1. Найти область сходимости ряда Решение. Обозначим а) если б) если признаку Лейбница, пример 1, лекция 3, разд. 3.1). Таким образом, область сходимости 4.2. Степенные ряды: основные понятия, теорема Абеля Рассмотрим частный случай функционального ряда, так называемый степенной ряд Определение 3. Степенным рядом называется функциональный ряд вида
где Степенной ряд есть «бесконечный многочлен», расположенный по возрастающим степеням Рассмотрим частный случай степенного ряда при Теорема 1 (теорема Абеля). 1) Если степенной ряд 2) Если же степенной ряд расходится при Доказательство. 1) По условию степенной ряд сходится в точке т. е. сходится числовой ряд
и по необходимому признаку сходимости его общий член стремится к 0, т.е. Рассмотрим теперь любое х, для которого Из неравенства
состоит из членов, которые больше соответствующих членов ряда (2). Ряд 2) Пусть ряд расходится числовой ряд фиксированном Следствие. Теорема Абеля позволяет судить о расположении точки сходимости степенного ряда. Если точка
Рис. 1. Интервалы сходимости и расходимости ряда Можно показать, что существует такое число Определение 4. Интервалом сходимости степенного ряда
Замечание. На концах интервала Покажем один из способов определения интервала и радиуса сходимости степенного ряда. Рассмотрим степенной ряд Составим ряд из абсолютных величин его членов:
и применим к нему признак Даламбера. Пусть существует
где
По признаку Даламбера ряд сходится, если
где Если окажется, что предел Для определения интервала и радиуса сходимости степенного ряда также можно использовать радикальный признак Коши, радиус сходимости ряда определяется из соотношения Определение 5. Обобщенным степенным рядом называется ряд вида
Покажем, как находится радиус сходимости для обобщенного степенного ряда.
т.е. Если Пример 2. Найти область сходимости ряда Решение. Обозначим
Решаем неравенство: сходимости имеет вид: Ответ: область сходимости Пример 3. Ряд Пример 4. Ряд Свойства степенных рядов Рассмотрим степенной ряд Свойство 1. Степенной ряд Свойство 2. Если отрезок
где Свойство 3. Сумма степенного ряда есть функция, имеющая внутри интервала сходимости производные любого порядка. Производные от суммы степенного ряда будут суммами рядов, полученных из данного степенного ряда почленным дифференцированием соответствующее число раз, причём радиусы сходимости таких рядов будут те же, что и у исходного ряда. Если Формула Тейлора Рассмотрим важную задачу, которая решается в теории функциональных рядов: по заданной функции найти сходящийся функциональный ряд того или иного типа, сумма которого в области сходимости равнялась бы заданной функции. Такая задача называется разложением функции в ряд, например, степенной. Пусть функция х 0: Задача: Подберём многочлен n -й степени
Коэффициенты многочлена
Для нахождения этих коэффициентов найдём производные до n -го порядка от
…
Подставим в эти соотношения
Находим выражения для
Получаем общую формулу для определения коэффициентов многочлена
Тогда многочлен примет следующий вид: по степеням Таким образом, для каждой функции Разность
Формула (5) называется формулой Тейлора для функции
Величина остаточного члена формулы Тейлора 1) Остаточный член в форме Пеано. Преобразуем остаточный член формулы Тейлора, используя некоторые понятия из теории пределов. а) Функция б) Бесконечно малая функция Рассмотрим формулу Тейлора для функции Формула Тейлора 2) Остаточный член в форме Лагранжа. Запишем остаточный член в виде
Рассмотрим частные случаи формулы Тейлора. – Если в формуле Тейлора с остаточным членом в форме Лагранжа положить – Если в формуле Тейлора положить
где остаточный член можно записать в форме Пеано:
Формула Маклорена является разложением функции Пример 5. Разложить функцию порядка по степеням Решение. Запишем формулу Тейлора для функции виде многочлена 3-го порядка с остаточным членом в форме Лагранжа
где Находим производные нужного порядка в точке
Полученные данные подставляем в формулу Тейлора Можно сказать, что функция
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1886; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.88.8 (0.013 с.) |

 , члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда
, члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда  является частичной суммой данного функционального ряда. Общий член
является частичной суммой данного функционального ряда. Общий член  есть функция от х, определённая в некоторой области. Рассмотрим функциональный ряд в точке
есть функция от х, определённая в некоторой области. Рассмотрим функциональный ряд в точке 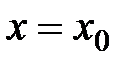 . Если соответствующий числовой ряд
. Если соответствующий числовой ряд  сходится, т.е. существует предел частичных сумм этого ряда
сходится, т.е. существует предел частичных сумм этого ряда  (где
(где  − сумма числового ряда), то точка
− сумма числового ряда), то точка  называется точкой сходимости функционального ряда
называется точкой сходимости функционального ряда  . Если числовой ряд
. Если числовой ряд  расходится, то точка
расходится, то точка  называется точкой расходимости функционального ряда.
называется точкой расходимости функционального ряда.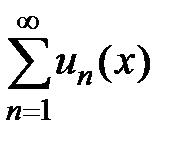 называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается
называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается  . Отметим, что
. Отметим, что  R.
R.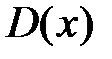 , если для любого
, если для любого  он сходится как числовой ряд, при этом его сумма будет некоторой функцией
он сходится как числовой ряд, при этом его сумма будет некоторой функцией  . Это так называемая предельная функция последовательности
. Это так называемая предельная функция последовательности  :
: 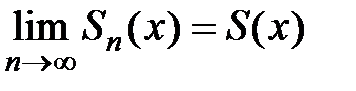 .
.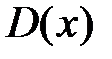 ? Можно использовать признак, аналогичный признаку Даламбера. Для ряда
? Можно использовать признак, аналогичный признаку Даламбера. Для ряда  составляем
составляем 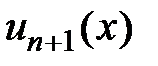 и рассматриваем предел при фиксированном х:
и рассматриваем предел при фиксированном х:  . Тогда
. Тогда 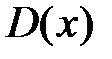 является решением неравенства
является решением неравенства  и решением уравнения
и решением уравнения  (берём только те решения уравнения, в
(берём только те решения уравнения, в .
. ,
,  . Составим и вычислим предел
. Составим и вычислим предел 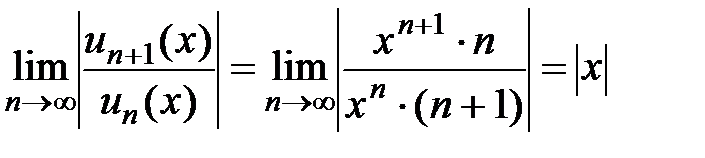 , тогда область сходимости ряда определяется неравенством
, тогда область сходимости ряда определяется неравенством  и уравнением
и уравнением  . Исследуем дополнительно сходимость исходного ряда в точках, являющимися корнями уравнения:
. Исследуем дополнительно сходимость исходного ряда в точках, являющимися корнями уравнения: ,
,  , то получается расходящийся ряд
, то получается расходящийся ряд 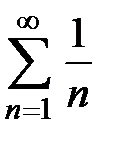 ;
;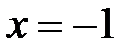 ,
,  , то ряд
, то ряд  сходится условно (по
сходится условно (по ряда
ряда  имеет вид:
имеет вид:  .
. , где
, где  .
. ,
, − постоянные числа, называемые коэффициентами ряда.
− постоянные числа, называемые коэффициентами ряда. . Любой числовой ряд
. Любой числовой ряд  является
является .
. :
: 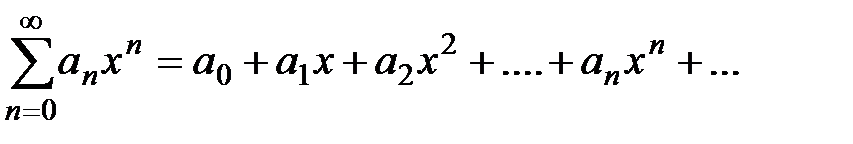 . Выясним, какой вид имеет
. Выясним, какой вид имеет .
. сходится в точке
сходится в точке 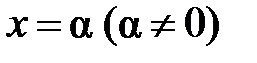 , то он абсолютно сходится при всяком х, для которого справедливо неравенство
, то он абсолютно сходится при всяком х, для которого справедливо неравенство  .
. , то он расходится при всяком х, для которого
, то он расходится при всяком х, для которого  .
. ,
,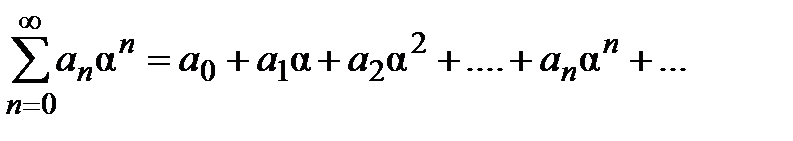 (1)
(1) . Следовательно, существует такое число
. Следовательно, существует такое число  , что все члены ряда ограничены этим числом:
, что все члены ряда ограничены этим числом: 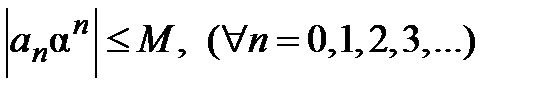 .
.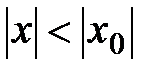 , и составим ряд из абсолютных величин:
, и составим ряд из абсолютных величин:  .
.  , то
, то  (2).
(2). получаем
получаем 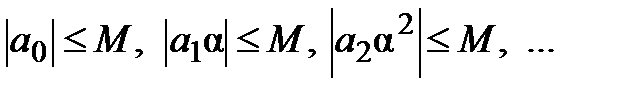 , т.е. ряд
, т.е. ряд (3)
(3) представляет собой сходящийся ряд геометрической прогрессии со знаменателем
представляет собой сходящийся ряд геометрической прогрессии со знаменателем  , причём
, причём 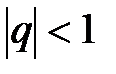 , так как
, так как  . Следовательно, ряд (2) сходится при
. Следовательно, ряд (2) сходится при  . Таким образом, степенной ряд
. Таким образом, степенной ряд 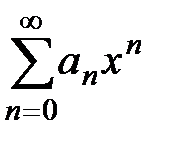 абсолютно сходится.
абсолютно сходится. расходится при
расходится при 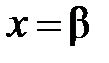 , иными словами,
, иными словами, . Докажем, что для любого х (
. Докажем, что для любого х ( ) ряд расходится. Доказательство ведётся от противного. Пусть при некотором
) ряд расходится. Доказательство ведётся от противного. Пусть при некотором (
(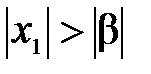 ) ряд сходится, тогда он сходится при всех
) ряд сходится, тогда он сходится при всех  (см. первую часть данной теоремы), в частности, при
(см. первую часть данной теоремы), в частности, при 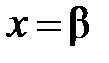 , что противоречит условию 2) теоремы 1. Теорема доказана.
, что противоречит условию 2) теоремы 1. Теорема доказана. является точкой сходимости степенного ряда, то интервал
является точкой сходимости степенного ряда, то интервал  заполнен точками сходимости; если точкой расходимости является точка
заполнен точками сходимости; если точкой расходимости является точка  , то
, то заполнены точками расходимости (рис. 1).
заполнены точками расходимости (рис. 1).
 , что при всех
, что при всех  степенной ряд
степенной ряд 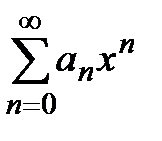 абсолютно сходится, а при
абсолютно сходится, а при  − расходится. Будем считать, что если ряд сходится только в одной точке 0, то
− расходится. Будем считать, что если ряд сходится только в одной точке 0, то  , а если ряд сходится при всех
, а если ряд сходится при всех  , то
, то  .
.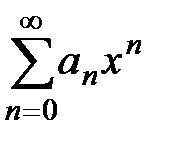 называется такой интервал
называется такой интервал  , что при всех
, что при всех  этот ряд сходится и притом абсолютно, а для всех х, лежащих вне этого интервала, ряд расходится. Число R называется радиусом сходимости степенного ряда.
этот ряд сходится и притом абсолютно, а для всех х, лежащих вне этого интервала, ряд расходится. Число R называется радиусом сходимости степенного ряда.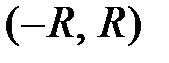 вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.
вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.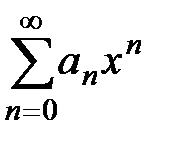 и обозначим
и обозначим 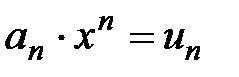 .
.
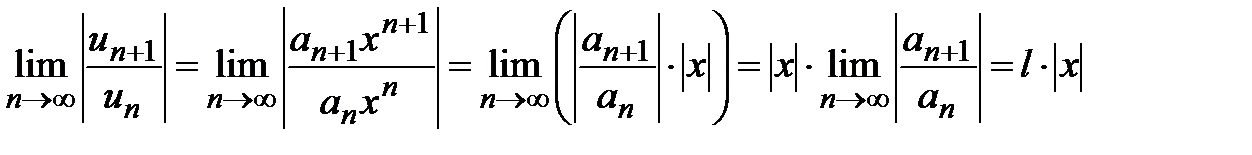 ,
, .
. , и расходится, если
, и расходится, если  . Отсюда ряд сходится при
. Отсюда ряд сходится при 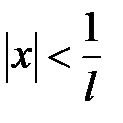 , тогда интервал сходимости:
, тогда интервал сходимости:  . При
. При  ряд расходится, так как
ряд расходится, так как  .
. , получим формулу для определения радиуса сходимости степенного ряда:
, получим формулу для определения радиуса сходимости степенного ряда: ,
,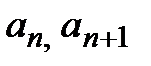 − коэффициенты степенного ряда.
− коэффициенты степенного ряда.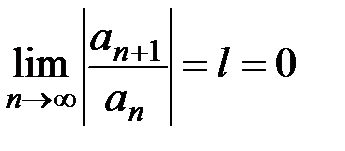 , то полагаем
, то полагаем  .
. .
. . Его также называют рядом по степеням
. Его также называют рядом по степеням  .
.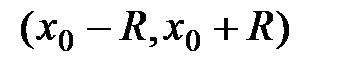 , где
, где  − радиус сходимости.
− радиус сходимости.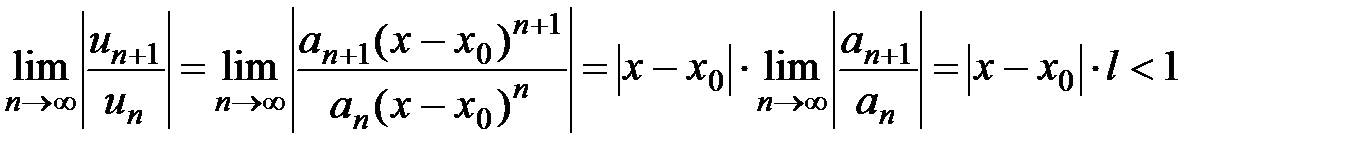 ,
, , где
, где  .
.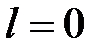 , то
, то  , и область сходимости
, и область сходимости 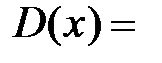 R; если
R; если  , то
, то  и область сходимости
и область сходимости 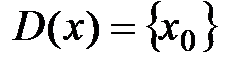 .
. .
. . Составим предел
. Составим предел .
. ,
, 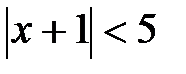 , следовательно, интервал
, следовательно, интервал , причём R = 5. Дополнительно исследуем концы интервала сходимости:
, причём R = 5. Дополнительно исследуем концы интервала сходимости: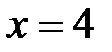 ,
,  , получаем ряд
, получаем ряд  , который расходится;
, который расходится;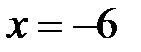 ,
,  , получаем ряд
, получаем ряд  , который сходится
, который сходится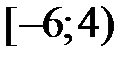 ,
,  .
.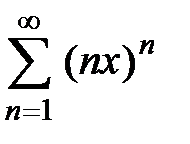 расходится для всех
расходится для всех  , так как
, так как  при
при  , радиус сходимости
, радиус сходимости  .
.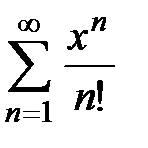 сходится при всех
сходится при всех  R, радиус сходимости
R, радиус сходимости  .
. , у которого интервал сходимости
, у которого интервал сходимости  , тогда сумма степенного ряда
, тогда сумма степенного ряда  определена для всех
определена для всех  и можно записать равенство
и можно записать равенство  .
. сходится абсолютно в любом промежутке
сходится абсолютно в любом промежутке  , лежащем в интервале сходимости, причём сумма степенного ряда
, лежащем в интервале сходимости, причём сумма степенного ряда  является непрерывной функцией при всех
является непрерывной функцией при всех  .
. , то степенной ряд можно
, то степенной ряд можно , то
, то .
. 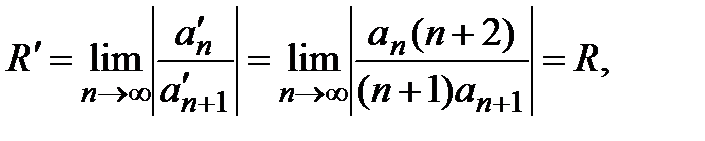
 − коэффициенты проинтегрированного ряда.
− коэффициенты проинтегрированного ряда. ,
, ,
, , …, и т.д.
, …, и т.д. определена в некоторой окрестности точки
определена в некоторой окрестности точки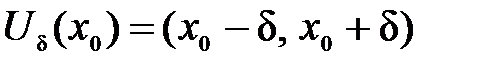 , где
, где  , причём в этой окрестности функция имеет все производные до
, причём в этой окрестности функция имеет все производные до  -го порядка.
-го порядка. по степеням
по степеням  так, чтобы в точке х 0 совпадали значения
так, чтобы в точке х 0 совпадали значения  и
и 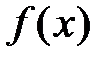 , а также значения их производных до (
, а также значения их производных до ( )-го порядка включительно. Тогда считаем, что в окрестности точки х 0 такой многочлен
)-го порядка включительно. Тогда считаем, что в окрестности точки х 0 такой многочлен  будет приближать данную функцию с некоторой точностью.
будет приближать данную функцию с некоторой точностью. являются неопределенными коэффициентами, которые необходимо найти исходя из следующих условий:
являются неопределенными коэффициентами, которые необходимо найти исходя из следующих условий: ,
,  ,
, 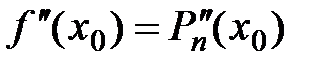 , …,
, …,  .
. :
: ,
, ,
, ,
, , при всех
, при всех  R.
R. и приравняем
и приравняем  , где
, где  :
: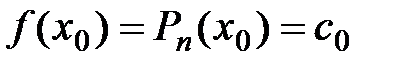 ,
,  ,
,  ,
, , …
, …  .
.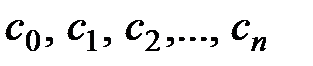 , решая полученную систему уравнений:
, решая полученную систему уравнений: .
. :
: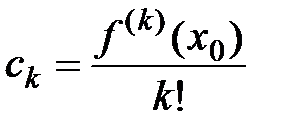 ,
,  . (4)
. (4)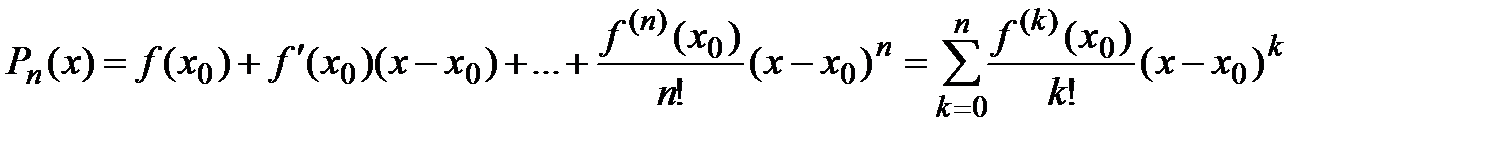 .
.
 , где
, где  называются коэффициентами многочлена Тейлора,
называются коэффициентами многочлена Тейлора,  .
. , удовлетворяющей поставленным условиям при
, удовлетворяющей поставленным условиям при  , можно найти многочлен Тейлора
, можно найти многочлен Тейлора  (в точке х 0 функция
(в точке х 0 функция  совпадают со своими производными до n -го порядка).
совпадают со своими производными до n -го порядка). , обозначенную через
, обозначенную через 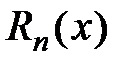 , называют остаточным членом формулы Тейлора, которая имеет вид:
, называют остаточным членом формулы Тейлора, которая имеет вид: (5)
(5) по степеням
по степеням  порядка n. Отметим, что
порядка n. Отметим, что .
. играет важную роль в оценке точности приближения заданной функции многочленом Тейлора. Существует два вида остаточных членов.
играет важную роль в оценке точности приближения заданной функции многочленом Тейлора. Существует два вида остаточных членов. называется бесконечно малой при
называется бесконечно малой при  , если
, если  .
.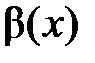 называется бесконечно малой более высокого порядка малости относительно бесконечно малой функции
называется бесконечно малой более высокого порядка малости относительно бесконечно малой функции  при
при  , если существует
, если существует  и записывается следующим образом:
и записывается следующим образом:  (что читается так: «β есть о малое от α).
(что читается так: «β есть о малое от α).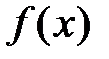 по степеням
по степеням 
 . Остаточный член в формуле Тейлора имеет вид:
. Остаточный член в формуле Тейлора имеет вид:  . Из построения многочлена Тейлора следует
. Из построения многочлена Тейлора следует  Тогда
Тогда 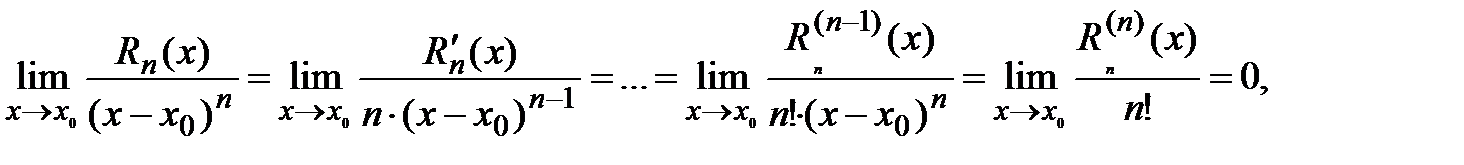 откуда остаточный член формулы Тейлора можно записать в виде:
откуда остаточный член формулы Тейлора можно записать в виде:  , т.е. величина остаточного члена есть бесконечно малая более высокого порядка малости относительно
, т.е. величина остаточного члена есть бесконечно малая более высокого порядка малости относительно  при
при  .
. , в которой
, в которой  ,
,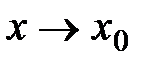 является бесконечно малой величиной, то можно считать, что разность
является бесконечно малой величиной, то можно считать, что разность  бесконечно мала, т.е.
бесконечно мала, т.е. 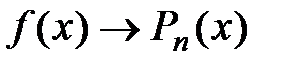 .
. , где Q (x) есть некоторая функция, подлежащая определению. Можно доказать, что
, где Q (x) есть некоторая функция, подлежащая определению. Можно доказать, что  , где точка ξ заключена между х и х 0:
, где точка ξ заключена между х и х 0: 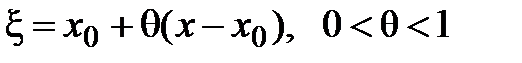 , т.е. остаточный член имеет вид:
, т.е. остаточный член имеет вид:  . Тогда формула Тейлора примет вид
. Тогда формула Тейлора примет вид  , который называется формулой Тейлора с остаточным членом в форме Лагранжа.
, который называется формулой Тейлора с остаточным членом в форме Лагранжа.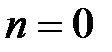 , то получаем формулу конечного приращения:
, то получаем формулу конечного приращения: 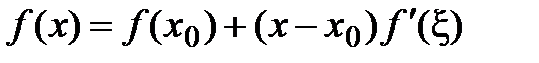 (теорема Лагранжа).
(теорема Лагранжа). , то получим формулу, которую называют формулой Маклорена:
, то получим формулу, которую называют формулой Маклорена: ,
,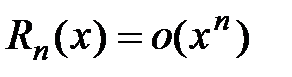 или в форме Лагранжа:
или в форме Лагранжа: .
. в виде многочлена по степеням х.
в виде многочлена по степеням х.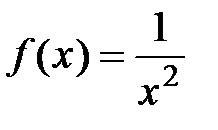 в виде многочлена третьего
в виде многочлена третьего с остаточным членом в форме Лагранжа.
с остаточным членом в форме Лагранжа. в точке
в точке  в
в ,
, .
. :
: ,
,  ;
;  ,
,  ;
;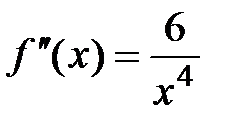 ,
,  ;
; 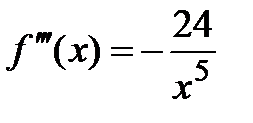 ,
,  ;
; 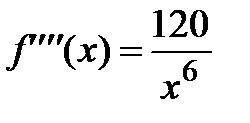 ,
,  , где
, где 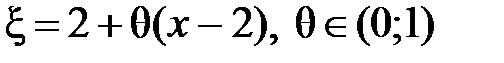 .
. и вычисляем
и вычисляем 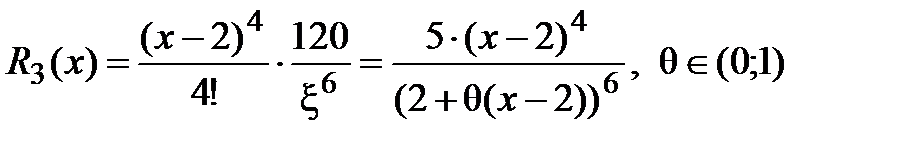 .
.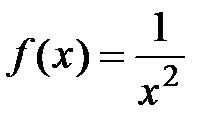 заменяется многочленом с точностью, которую можно определить, оценив остаточный член формулы Тейлора
заменяется многочленом с точностью, которую можно определить, оценив остаточный член формулы Тейлора  при
при  .
.


