
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение функций в степенные рядыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Если функция f(x) имеет на некотором интервале, содержащем точку а, производные всех порядков, то к ней может быть применена формула Тейлора:
где rn – так называемый остаточный член или остаток ряда, его можно оценить с помощью формулы Лагранжа:
Если для некоторого значения х rn ®0 при n ®¥, то в пределе формула Тейлора превращается для этого значения в сходящийся ряд Тейлора:
Таким образом, функция f(x) может быть разложена в ряд Тейлора в рассматриваемой точке х, если: 1) она имеет производные всех порядков; 2) построенный ряд сходится в этой точке.
При а =0 получаем ряд, называемый рядом Маклорена:
Пример 1. Разложить в степенной ряд функцию f(x)= 2 x. Решение. Найдем значения функции и ее производных при х =0 f(x) = 2 x, f( 0 ) = 2 0 =1; f¢(x) = 2 x ln2, f¢( 0 ) = 2 0 ln2= ln2; f¢¢(x) = 2 x ln22, f¢¢( 0 ) = 2 0 ln22= ln22; … f(n)(x) = 2 x ln n 2, f(n)( 0 ) = 2 0 ln n 2= ln n 2. Подставляя полученные значения производных в формулу ряда Тейлора, получим:
Радиус сходимости этого ряда равен бесконечности, поэтому данное разложение справедливо для -¥< x <+¥.
Пример 2. Написать ряд Тейлора по степеням (х +4) для функции f(x)= e x. Решение. Находим производные функции e x и их значения в точке х =-4. f(x) = е x, f( -4 ) = е -4; f¢(x) = е x, f¢( -4 ) = е -4; f¢¢(x) = е x, f¢¢( -4 ) = е -4; … f(n)(x) = е x, f(n)( -4 ) = е -4. Следовательно, искомый ряд Тейлора функции имеет вид:
Данное разложение также справедливо для -¥< x <+¥.
Пример 3. Разложить функцию f(x) =ln x в ряд по степеням (х- 1), (т.е. в ряд Тейлора в окрестности точки х =1). Решение. Находим производные данной функции.
…
Подставляя эти значения в формулу, получим искомый ряд Тейлора:
С помощью признака Даламбера можно убедиться, что ряд сходится при ½ х- 1½<1. Действительно,
Ряд сходится, если ½ х- 1½<1, т.е. при 0< x <2. При х =2 получаем знакочередующийся ряд, удовлетворяющий условиям признака Лейбница. При х =0 функция не определена. Таким образом, областью сходимости ряда Тейлора является полуоткрытый промежуток (0;2].
Приведем полученные подобным образом разложения в ряд Маклорена (т.е. в окрестности точки х =0) для некоторых элементарных функций: (1) (2) (3) (4) (5) ( последнее разложение называют биномиальным рядом)
Пример 4. Разложить в степенной ряд функцию Решение. В разложении (1) заменяем х на – х 2, получаем:
Пример 5. Разложить в ряд Маклорена функцию Решение. Имеем Пользуясь формулой (4), можем записать:
подставляя вместо х в формулу –х, получим:
Отсюда находим:
Раскрывая скобки, переставляя члены ряда и делая приведение подобных слагаемых, получим
(-1;1), так как он получен из двух рядов, каждый из которых сходится в этом интервале.
Замечание. Формулами (1)-(5) можно пользоваться и для разложения соответствующих функций в ряд Тейлора, т.е. для разложения функций по целым положительным степеням (х-а). Для этого над заданной функцией необходимо произвести такие тождественные преобразования, чтобы получить одну из функций (1)-(5), в которой вместо х стоит k(х-а)m, где k – постоянное число, m – целое положительное число. Часто при этом удобно сделать замену переменной t = х-а и раскладывать полученную функцию относительно t в ряд Маклорена. Этот метод иллюстрирует теорему о единственности разложения функции в степенной ряд. Сущность этой теоремы состоит в том, что в окрестности одной и той же точки не может быть получено два различных степенных ряда, которые бы сходились к одной и той же функции, каким бы способом ее разложение ни производилось.
Пример 6. Разложить функцию Решение. Эту задачу можно решить, как и раньше, с помощью определения ряда Тейлора, для чего нужно найти производные функции и их значения при х =3. Однако проще будет воспользоваться имеющимся разложением (5):
Полученный ряд сходится при
Пример 7. Написать ряд Тейлора по степеням (х -1) функции Решение.
Ряд сходится при
Пример 8. Разложить функцию Решение. Сделаем замену t = х -2:
Воспользовавшись разложением (3), в котором на место х подставим
Полученный ряд сходится к заданной функции при Таким образом,
Решить: Разложить заданную функцию в ряд: A 1) 3)
5) 7) 9)
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 11303; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.86.74 (0.008 с.) |

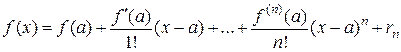 ,
, , где число x заключено между х и а.
, где число x заключено между х и а.



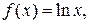
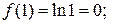
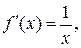











 ,
,
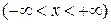 ,
,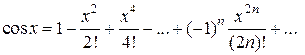

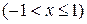 ,
,

 .
.
 .
.

 ;
;


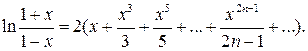 Этот ряд сходится в интервале
Этот ряд сходится в интервале в ряд Тейлора в окрестности точки х =3.
в ряд Тейлора в окрестности точки х =3.

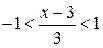 или –3< x- 3<3, 0< x < 6 и является искомым рядом Тейлора для данной функции.
или –3< x- 3<3, 0< x < 6 и является искомым рядом Тейлора для данной функции. .
.
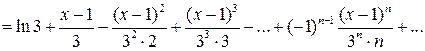
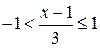 , или -2 < x £ 5.
, или -2 < x £ 5. в ряд Тейлора в окрестности точки x= 2.
в ряд Тейлора в окрестности точки x= 2. .
.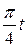 , получим:
, получим:
 , т.е. при
, т.е. при  .
.
 по степеням х 2)
по степеням х 2)  по степеням х
по степеням х по степеням х 4)
по степеням х 4)  по степеням х
по степеням х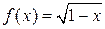 по степеням (х+ 1)6)
по степеням (х+ 1)6)  по степ. х 8)
по степ. х 8)  в ряд Маклорена
в ряд Маклорена в ряд Маклорена 10)
в ряд Маклорена 10)  в ряд Маклорена
в ряд Маклорена


