
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенные вычисления с помощью рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Степенные ряды широко используются в приближенных вычислениях. С их помощью с заданной точностью можно вычислять значения корней, тригонометрических функций, логарифмов чисел, определенных интегралов. Ряды применяются также при интегрировании дифференциальных уравнений.
Приближенное вычисление значений функций
Рассмотрим разложение функции в степенной ряд:
Для того, чтобы вычислить приближенное значение функции в заданной точке х, принадлежащей области сходимости указанного ряда, в ее разложении оставляют первые n членов (n – конечное число), а остальные слагаемые отбрасывают:
Для оценки погрешности полученного приближенного значения необходимо оценить отброшенный остаток rn (x). Для этого применяют следующие приемы: - если полученный ряд является знакочередующимся, то используется следующее свойство: для знакочередующегося ряда, удовлетворяющего условиям Лейбница, остаток ряда по абсолютной величине не превосходит первого отброшенного члена. - если данный ряд знакопостоянный, то ряд, составленный из отброшенных членов, сравнивают с бесконечно убывающей геометрической прогрессией. - в общем случае для оценки остатка ряда Тейлора можно воспользоваться формулой Лагранжа:
Пример 1. Пользуясь разложением в ряд sin x, вычислить sin20o с точностью до 0,0001. Решение. Чтобы можно было пользоваться формулой (2), необходимо выразить значение аргумента в радианной мере. Получаем
Полученный ряд является знакочередующимся и удовлетворяет условиям Лейбница. Так как
Пример 2. Вычислить Решение. Воспользуемся разложением
Проверим, можем ли мы отбросить остаток после первых трех членов разложения, для этого оценим его с помощью суммы бесконечно убывающей геометрической прогрессии:
Таким образом, мы можем отбросить этот остаток и получаем
Пример 3. Вычислить Решение. Воспользуемся биномиальным рядом. Так как 53 является ближайшим к 130 кубом целого числа, то целесообразно число 130 представить в виде 130=53+5.
так как уже четвертый член полученного знакочередующегося ряда, удовлетворяющего признаку Лейбница, меньше требуемой точности:
Приближенное вычисление определенных интегралов
Многие практически нужные определенные или несобственные интегралы не могут быть вычислены с помощью формулы Ньютона-Лейбница, ибо ее применение связано с нахождением первообразной, часто не имеющей выражения в элементарных функциях. Бывает также, что нахождение первообразной возможно, но излишне трудоемко. Однако если подинтегральная функция раскладывается в степенной ряд, а пределы интегрирования принадлежат интервалу сходимости этого ряда, то возможно приближенное вычисление интеграла с наперед заданной точностью. Пример 4: Вычислить интеграл Решение. Соответствующий неопределенный интеграл Разделив почленно ряд для sin x на x, получим:
Интегрируя этот ряд почленно (это возможно, так как пределы интегрирования принадлежат интервалу сходимости данного ряда), получаем:
Так как полученный ряд удовлетворяет условиям Лейбница и Таким образом, находим
Пример 5. Вычислить интеграл Решение.
Проверим, можем ли мы отбросить остаток после второго члена полученного ряда.
Следовательно,
Приближенное решение задачи Коши для обыкновенного Дифференциального уравнения
В частых случаях, когда ОДУ не решается в общем виде, решить задачу Коши для него можно приближенно, в виде первых нескольких членов разложения решения в ряд Тейлора (в окрестности данной точки)
Пример Найти первые 3 члена разложения в ряд решения задачи Коши
Решение: Будем искать решение задачи в виде
Коэффициент у (1)=2 – это начальное условие задачи Коши. Коэффициент
Продифференцируем обе части данного уравнения, чтобы найти
Таким образом, Решить: Вычислить приближенно с указанной точностью: A 1) 5) 8) 11) 14) B Найти первые несколько членов разложения в ряд решения задачи Коши: 17) y¢-4y+xy2-e2x=0; y(0)=2 (4 члена) 18) y¢+ycosx-y2sinx=0; y(p)=1 (4 члена) 19) y¢¢=eycosy¢; y(1)=1; y¢(1)=p/6 (5 членов) 20) y¢¢=xy2-1/y¢; y(0)=0, y¢(0)=1 (5 членов) Ряд Фурье
Рядом Фурье функции f (x) на интервале (-p;p) называется тригонометрический ряд вида:
Рядом Фурье функции f (x) на интервале (- l; l) называется тригонометрический ряд вида:
Ряд Фурье кусочно-непрерывной, кусочно-монотонной и ограниченной на интервале (- l; l) функции сходится на всей числовой оси. Сумма ряда Фурье S (x): - является периодической функцией с периодом 2 l - на интервале (- l; l) совпадает с функцией f (x), за исключением точек разрыва - в точках разрыва (первого рода, т.к. функция ограничена) функции f (x) и на концах интервала принимает средние значения:
Говорят, что функция раскладывается в ряд Фурье на интервале(- l; l):
Если f (x) – четная функция, то в ее разложении участвуют только четные функции, то есть bn =0. Если f (x) – нечетная функция, то в ее разложении участвуют только нечетные функции, то есть аn =0
Рядом Фурье функции f (x) на интервале (0; l) по косинусам кратных дуг называется ряд:
Рядом Фурье функции f (x) на интервале (0; l) по синусам кратных дуг называется ряд:
Сумма ряда Фурье по косинусам кратных дуг является четной периодической функцией с периодом 2 l, совпадающей с f (x) на интервале (0; l) в точках непрерывности. Сумма ряда Фурье по синусам кратных дуг является нечетной периодической функцией с периодом 2 l, совпадающей с f (x) на интервале (0; l) в точках непрерывности.
Ряд Фурье для данной функции на данном интервале обладает свойством единственности, то есть если разложение получено каким-либо иным способом, чем использование формул, например, при помощи подбора коэффициентов, то эти коэффициенты совпадают с вычисленными по формулам.
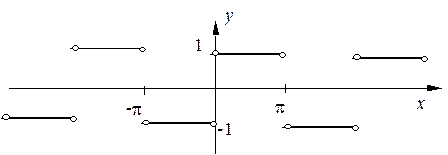
Примеры. 1. Разложить функцию f (x)=1: а) в полный ряд Фурье на интервале (-p;p); б) в ряд по синусам кратных дуг на интервале (0;p); построить график полученного ряда Фурье Решение: а) Разложение в ряд Фурье на интервале(-p;p) имеет вид:
причем все коэффициенты bn =0, т.к. данная функция – четная; таким образом,
Очевидно, равенство будет выполнено, если принять а 0=2, а 1= а 2= а 3=…=0 В силу свойства единственности это и есть искомые коэффициенты. Таким образом, искомое разложение: В таком случае, когда ряд тождественно совпадает со своей функцией, график ряда Фурье совпадает с графиком функции на всей числовой прямой. б) Разложение на интервале (0;p) по синусам кратных дуг имеет вид:
Подобрать коэффициенты так, чтобы равенство тождественно выполнялось, очевидно, невозможно. Воспользуемся формулой для вычисления коэффициентов:
Таким образом, для четных n (n =2 k) имеем bn =0, для нечетных (n =2 k -1) - Окончательно, Построим график полученного ряда Фурье, воспользовавшись его свойствами (см. выше). Прежде всего, строим график данной функции на заданном интервале. Далее, воспользовавшись нечетностью суммы ряда, продолжаем график симметрично началу координат:
Продолжаем периодическим образом на всей числовой оси:
И наконец, в точках разрыва заполняем средние (между правым и левым пределом) значения:
2. Разложить функцию Решение: Искомое разложение имеет вид:
Коэффициенты ряда можно подобрать, если ряд в правой части равенства содержит такие же слагаемые, как функция в левой части. Поскольку и левая, и правая части равенства содержат только функции sin от различных аргументов, следует проверить, совпадают ли при каких-либо значениях n (натуральных!) аргументы синусов в левой и правой частях равенства:
Таким образом, при помощи подбора коэффициентов удалось получить искомое разложение:
Решить: Разложить данную функцию на указанном интервале в ряд Фурье. Построить график суммы полученного ряда (кроме задач 4,8,12) A 1. 3. 4. 5. 6. 7. 8. 9. 11. B 13. 15.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 13492; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.171.86 (0.007 с.) |

 .
. .
. (или x<c<a).
(или x<c<a). . Подставляя это значение в формулу, получаем
. Подставляя это значение в формулу, получаем
 , то этот и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом,
, то этот и все последующие члены ряда можно отбросить, ограничиваясь первыми двумя членами. Таким образом, .
. с точностью до 0,01.
с точностью до 0,01. , где
, где  (см. пример 5 в предыдущей теме):
(см. пример 5 в предыдущей теме):
 .
. .
.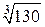 с точностью до 0,0001.
с точностью до 0,0001.

 ,
, , поэтому его и следующие за ним члены можно отбросить.
, поэтому его и следующие за ним члены можно отбросить.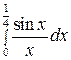 с точностью до 0,00001.
с точностью до 0,00001. не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.
не может быть выражен в элементарных функциях, т.е. представляет собой «неберущийся интеграл». Применить формулу Ньютона-Лейбница здесь нельзя. Вычислим интеграл приближенно.


 достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью.
достаточно взять сумму первых двух членов, чтобы получить искомое значение с заданной точностью. .
. с точностью до 0,001.
с точностью до 0,001.
 .
. .
. до 0,001
до 0,001
 найдем из уравнения, подставив в него начальные условия:
найдем из уравнения, подставив в него начальные условия:
 :
: ;
;
 .
.
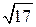 до 0,0001 2)
до 0,0001 2)  до 0,0001 3)
до 0,0001 3)  до 0,01 4) ln6 до 0,01
до 0,01 4) ln6 до 0,01 до 0,001 6)
до 0,001 6)  до 0,001 7)
до 0,001 7)  до 0,01
до 0,01 до 0,001 9)
до 0,001 9)  до 0,001 10)
до 0,001 10)  до 0,001
до 0,001 до 0,001 12)
до 0,001 12)  до 0,01 13)
до 0,01 13)  до 0,001
до 0,001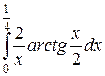 до 0,001 15)
до 0,001 15)  до 0,001 16)
до 0,001 16)  до 0,001
до 0,001 , где
, где .
.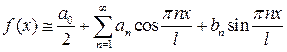 , где
, где .
.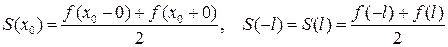 .
. .
. , где
, где 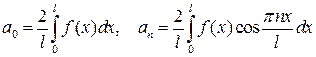 .
. , где
, где  .
. ,
,
 или просто 1=1.
или просто 1=1.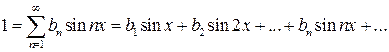
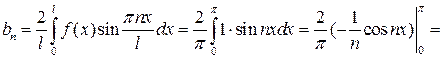


 .
.


 на интервале (0;6) по синусам кратных дуг
на интервале (0;6) по синусам кратных дуг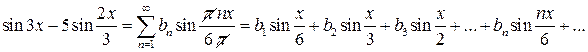
 или
или  , откуда n =18. Значит, такое слагаемое содержится в правой части и коэффициент при нем должен совпадать с коэффициентом в левой части: b 18=1;
, откуда n =18. Значит, такое слагаемое содержится в правой части и коэффициент при нем должен совпадать с коэффициентом в левой части: b 18=1; или
или  , откуда n =4. Значит, b 4=-5.
, откуда n =4. Значит, b 4=-5.
 на (0;1) по синусам кратных дуг; 2.
на (0;1) по синусам кратных дуг; 2.  на (-p;p)
на (-p;p) на (-3;3)
на (-3;3) на (0;p) по косинусам кратных дуг
на (0;p) по косинусам кратных дуг на (-2;2)
на (-2;2) на (0;p) по косинусам кратных дуг
на (0;p) по косинусам кратных дуг на (0;4p) по синусам кратных дуг
на (0;4p) по синусам кратных дуг на (-p;p); 10.
на (-p;p); 10.  на (0;5) по синусам
на (0;5) по синусам на (-2;2); 12.
на (-2;2); 12.  на (-10p;10p)
на (-10p;10p)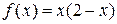 на (0;2) по синусам; 14.
на (0;2) по синусам; 14.  на (0;6) по синусам
на (0;6) по синусам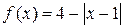 на (0;5) по косинусам; 16.
на (0;5) по косинусам; 16.  на (0;1) по косинусам
на (0;1) по косинусам


