
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление погрешности средней проницаемостиСодержание книги Поиск на нашем сайте
Величины средней проницаемости и ее дисперсии, вычисленные в предыдущем пункте по формулам (2.1) и (2.6), являются приближенными, т.к. они получены по ограниченному числу измерений. В этом разделе рассмотрим способ вычисления величины погрешности, с которой определена средняя проницаемость (2.2). Поскольку дисперсия характеризует ширину распределения, или более конкретно, степень отклонения имеющейся совокупности данных от средней величины, то она является мерой абсолютной погрешности
В соответствующей литературе эту величину называют по-разному - среднеквадратичным отклонением, среднеквадратичной погрешностью или стандартом. Стандарт
Вычислим теперь дисперсию средних величин
Следовательно, величина относительной погрешности распределения средних проницаемостей равна
т. е., относительная погрешность распределения средних проницаемостей, в
Величину абсолютной погрешности
т.е. она определена с относительной погрешностью
Изложенный способ вычисления погрешности средней проницаемости используется часто, но следует отметить, что он является приближенным и имеет оценочный характер. При более строгом рассмотрении вопроса вычисления погрешности
Это равенство означает, что с вероятностью
Вероятность Рассмотрим теперь общий случай. До сих пор мы рассматривали величину
где
т.е. полная площадь под функцией плотности вероятностей нормального распределения равна единице, или, применяя стандартную терминологию, следует сказать, что эта функция нормирована. Поскольку, в рассматриваемом нами примере, проницаемость
Из (3.8) и (3.9) следует, что измеренная в одной серии опытов средняя проницаемость
Перепишем (3.10) используя (3.5) и (3.9)
Приравнивая правые части (2.11) и (3.11) получаем уравнение для границ доверительного интервала
откуда
где Как уже отмечалось, истинное значение
где Используя результаты, приведенные в табл. 2 можно сказать, что средняя проницаемость горных пород, определяемая по данным табл. 1, с доверительной вероятностью
Из табл. 2 следует, что чем больше доверительная вероятность Таблица 2
Таким образом, мы рассмотрели приближенный метод построения доверительного интервала, не зная при этом истинного закона
где
Например, если бы распределение проницаемостей
Заключение Мы выработали и углубили знания о проницаемости горных пород.Проницаемость – важнейший параметр, характеризующий проводимость коллектора, т. е. способность пород пласта пропускать к забоям скважин нефть и газ при наличии перепада между пластовым и забойным давлениями. Под абсолютной принято понимать проницаемость пористой среды, которая определена при наличии в ней лишь одной какой либо фазы, химически инертной по отношению к породе. Под абсолютной принято понимать проницаемость пористой среды, которая определена при наличии в ней лишь одной какой либо фазы, химически инертной по отношению к породе. Относительной проницаемостью пористой среды называется отношение фазовой проницаемости этой среды к абсолютной.
В системе СИ коэффициент проницаемости измеряется в м2; в системе СГС [kпр] = см2; в системе НПГ (нефтепромысловой геологии) [kпр] = Д (Дарси). 1 Дарси = 1,02×10-8 см2 = 1,02 · 10-12 м2» 1 мкм2. Научились определять проницаемости горных пород, распределять по интервалам и вычислять погрешности. Экспериментальные установки для изучения относительной проницаемости среды более сложны, так как при этом необходимо моделировать многофазный поток, регистрировать насыщенность порового пространства различными фазами и регистрировать расход нескольких фаз.
Список литературы 1. Гиматудинов Ш.К. Справочная книга по добыче нефти. Под ред. д-ра техн. наук Гиматудинова Ш.К. Недра 1974.- 704с. 2. Медведев Ю.А. Физика нефтяного и газового пласта: Курс лекций. Тюмень: ТюмГНГУ, 2000 – 158с. 3. Медведев Ю.А., Филин В.В., Методические указания: к выполнению курсовых проектов, курсовых и квалификационных работ для студентов очного обучения направления 650700 ''Нефтегазовое дело'', ТГНГУ 2001г. – 32с. 4. Сидоровский В.А., Вскрытие пластов и повышение продуктивности пластов. Недра 1978г. – 256с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 500; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.201.101 (0.011 с.) |

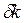 в определении средней проницаемости
в определении средней проницаемости  (величину
(величину 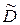 с погрешностью
с погрешностью 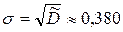 (3.1)
(3.1)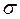 характеризует вероятность попадания величины проницаемости одной случайно выбранной породы в интервал
характеризует вероятность попадания величины проницаемости одной случайно выбранной породы в интервал 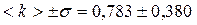 . Величина
. Величина 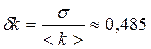 называется относительной погрешностью или относительной дисперсией. Но это только частный случай. В общем случае величина
называется относительной погрешностью или относительной дисперсией. Но это только частный случай. В общем случае величина  . Это означает, что погрешность
. Это означает, что погрешность 
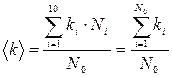 .
.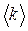 . Используя свойства дисперсий, приведенные в конце предыдущего пункта получаем
. Используя свойства дисперсий, приведенные в конце предыдущего пункта получаем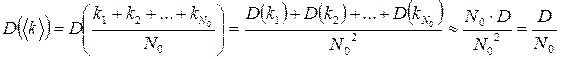 .
. ,
,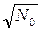 раз меньше относительной погрешности одного отдельного измерения. Следовательно, с ростом числа испытуемых пород
раз меньше относительной погрешности одного отдельного измерения. Следовательно, с ростом числа испытуемых пород  . (3.2)
. (3.2)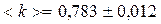 , (3.3)
, (3.3)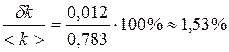 . (3.4)
. (3.4) .
.  . Пусть истинная средняя проницаемость
. Пусть истинная средняя проницаемость 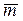 пород отличается от вычисленной величины
пород отличается от вычисленной величины  с вероятностью
с вероятностью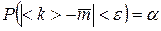 .
.  . (3.6)
. (3.6)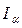 - доверительным интервалом.
- доверительным интервалом.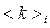 , вычисленной по формуле (2.1). Тогда, согласно центральной предельной теореме теории вероятностей, распределение по числу полученных средних
, вычисленной по формуле (2.1). Тогда, согласно центральной предельной теореме теории вероятностей, распределение по числу полученных средних 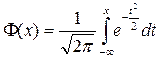 , (3.7)
, (3.7)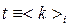 . Эта функция представляет собой нормальную функцию распределения с параметрами
. Эта функция представляет собой нормальную функцию распределения с параметрами  и
и 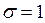 , и характеризует вероятность того, что случайно выбранная величина
, и характеризует вероятность того, что случайно выбранная величина 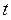 имеет значение, меньшее чем
имеет значение, меньшее чем 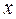 (см. Приложение). Здесь отметим, что
(см. Приложение). Здесь отметим, что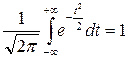 , (3.8)
, (3.8) является положительной величиной, то величины
является положительной величиной, то величины 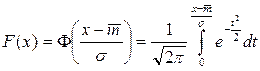 . (3.9)
. (3.9)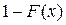 . Эта вероятность соответствует затененной части площади под функцией плотности вероятностей. Тогда в силу симметрии рассматриваемой функции, величина
. Эта вероятность соответствует затененной части площади под функцией плотности вероятностей. Тогда в силу симметрии рассматриваемой функции, величина 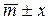 с вероятностью
с вероятностью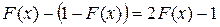 . (3.10)
. (3.10)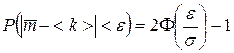 . (3.11)
. (3.11)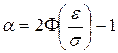 ,
,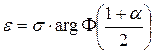 , (3.12)
, (3.12)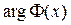 - функция, обратная
- функция, обратная 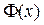 .
.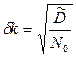 , определяемое из опыта. Вычисляя, таким образом, величину
, определяемое из опыта. Вычисляя, таким образом, величину  в зависимости от
в зависимости от 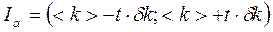 , (3.13)
, (3.13) попадает в интервал с доверительными границами
попадает в интервал с доверительными границами 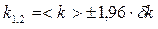 :
: ,
,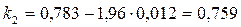 .
.
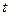
 распределения проницаемостей пород. В том случае, когда этот закон известен, задача построения доверительного интервала решается точно, т.к. при вычислении дисперсии, мы вместо (2.6) можем пользоваться точной формулой
распределения проницаемостей пород. В том случае, когда этот закон известен, задача построения доверительного интервала решается точно, т.к. при вычислении дисперсии, мы вместо (2.6) можем пользоваться точной формулой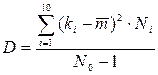 , (3.14)
, (3.14)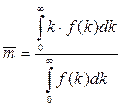 . (3.15)
. (3.15)


