
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графическое представление данных и их характеристикиСодержание книги
Поиск на нашем сайте
В качестве численных характеристик гистограмм чаще всего рассматривают два параметра – среднюю величину и дисперсию, и реже используют такие величины как наиболее вероятная и медиана. Определим два последних понятия. Наиболее вероятная величина распределения определяется как значение переменной, на которую приходится максимум распределения. Медианой называют такое значение переменной, относительно которой полная площадь под распределением делится на две равные части. В идеальном эксперименте, когда проводится большое число высокоточных измерений, средняя величина совпадает с т.н. математическим ожиданием. Средняя величина характеризует положение центра тяжести гистограммы на оси абсцисс, а дисперсия - ширину распределения вдоль нее. Вычислим эти характеристики по данным табл. 1. По определению, средняя величина проницаемости есть
где
Формула (2.1) применяется для вычисления средней величины в случае, когда исходные данные предварительно распределены по отдельным ячейкам, т.е. в виде табл. 1. В этом случае мы не располагаем данными по отдельно взятым породам. В случае, когда известны проницаемости каждой из тысячи рассмотренных пород, средняя проницаемость вычисляется как средняя арифметическая
Таким образом, мы вычислили среднюю проницаемость горных пород, хотя и для достаточно большой, но ограниченной выборки пород
где В формуле (2.3) математическое ожидание
Применим эту формулу к данным табл. 1.
Здесь отметим, что формулы (2.3) и (2.4), вообще говоря, являются приближенными. Они справедливы только в случае больших значений
Отличие знаменателей правых частей формул (2.6) и (2.4) обусловлено тем, что сумма в числителе должна быть отнесена не к числу образцов Как уже отмечалось, дисперсия является одной из важнейших характеристик статистического распределения, и характеризует ее ширину. Она обладает следующими важными свойствами (без доказательства).
1. Дисперсия постоянной величины равна нулю: 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 3. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсий этих величин:
|
||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 516; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.28.90 (0.009 с.) |

 , (2.1)
, (2.1)


 (2.2)
(2.2) .
. . Поэтому, полученная величина
. Поэтому, полученная величина  является приближенной. Поясним сказанное. Предположим, что у нас имеется возможность выбора образцов горных пород из неограниченно большого набора пород. Результат (2.2) получен для одной выборки, состоящей из 1000 образцов. Если проделать аналогичную процедуру для другой выборки из 1000 образцов, то получаемый результат может оказаться близким, но не совпадающим с (2.2). Увеличивая, таким образом, число исследуемых образцов в одной выборке можно повысить точность определения величины средней проницаемости. При бесконечно большом числе исследуемых образцов эта величина неограниченно приближается к истинной средней величине
является приближенной. Поясним сказанное. Предположим, что у нас имеется возможность выбора образцов горных пород из неограниченно большого набора пород. Результат (2.2) получен для одной выборки, состоящей из 1000 образцов. Если проделать аналогичную процедуру для другой выборки из 1000 образцов, то получаемый результат может оказаться близким, но не совпадающим с (2.2). Увеличивая, таким образом, число исследуемых образцов в одной выборке можно повысить точность определения величины средней проницаемости. При бесконечно большом числе исследуемых образцов эта величина неограниченно приближается к истинной средней величине 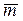 , т.е. к математическому ожиданию. Поскольку величина
, т.е. к математическому ожиданию. Поскольку величина  , (2.3)
, (2.3)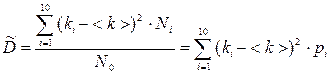 . (2.4)
. (2.4)


 .
. . (2.5)
. (2.5) . Для сравнительно малых значений
. Для сравнительно малых значений  . (2.6)
. (2.6) . Здесь можно предположить, что все 1000 измерений
. Здесь можно предположить, что все 1000 измерений 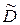 выражается через среднюю проницаемость
выражается через среднюю проницаемость  . В этом смысле величину
. В этом смысле величину  в (2.6) называют числом степеней свободы. Поскольку величина
в (2.6) называют числом степеней свободы. Поскольку величина  .
. .
. .
.


