
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение в ряд Маклорена некоторых функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Имеем
Областью сходимости этого степенного ряда является интервал 2. Имеем:
Очевидно, что производные четного порядка
Область сходимости ряда 3. Рассматривая аналогично функции
Область сходимости ряда 4. Имеем
При
Найдем интервал сходимости ряда: Ряд, составленный из модулей
Следовательно, интервал сходимости ряда Ряд (5.6) называется биномиальным. Если Выпишем некоторые разложения функции
Если в это разложение подставить
5. Получить разложение для этой функции, непосредственно вычисляя коэффициенты с помощью производных, не очень просто, поэтому мы воспользуемся разложением (5.7) и свойством 2) степенных рядов. Интегрируя почленно равенство (5.7) в интервале
Область сходимости ряда (после выяснения сходимости на концах интервала) есть 6. Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (5.8):
Область сходимости ряда 7. Воспользуемся разложением (5.10), подставив в него
Интегрируя в интервале
Область сходимости ряда Можно доказать, что ряды, приведенные в формулах (5.3) – (5.13), сходятся к функциям, для которых они составлены. При разложении более сложных функций часто используют готовые разложения (5.3) – (5.13). Примеры 1) Разложить в ряд Маклорена функцию Решение. Воспользуемся известной тригонометрической формулой Разложим в ряд Маклорена функцию
Тогда
Это и есть разложение в ряд Маклорена функции 2) Разложить в ряд Тейлора по степеням Решение. Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (5.7):
Полученное разложение справедливо, когда Применение рядов в приближенных вычислениях Степенные ряды имеют самые разнообразные приложения. С их помощью вычисляют с заданной степенью точности значения функций, определенных интегралов, которые являются «не берущимися» или слишком сложными для вычислений, интегрируются дифференциальные уравнения. Примеры I. Вычислить приближенно с точностью до 0,0001: а) Решение. Для вычисления
Взяв первые пять членов разложения, на основании следствия из теоремы Лейбница для сходящегося знакочередующегося ряда, мы допустим погрешность Итак, б) Решение. Воспользуемся разложением (5.11), подставив в него
Так как данный числовой ряд не является знакопеременным, то о погрешности нельзя судить по величине первого отбрасываемого члена. Если в качестве
Итак, в) Решение. Для вычисления
(необходимо взять два члена, так как при этом погрешность
II. Вычислить приближенно с точностью до 0,001 следующие интегралы: a) Решение. Так как интеграл «не берущийся», «точное» интегрирование здесь невозможно. Воспользуемся разложением (5.4). Разделив обе части на
Возьмем первые три члена разложения, т.к. Итак, б) Решение. Заменив
Умножая полученный ряд на
и почленно интегрируя в интервале
При этом Задачи Разложить в ряд Маклорена следующие функции, указав промежутки сходимости полученных рядов. 86. 89. 92. Разложить в ряд Тейлора следующие функции и найти область сходимости полученного ряда. 93. 94 95. 96. 97. 98. Вычислить приближенно с точностью до 0,0001: 99. 104. Вычислить приближенно, взяв первые два члена разложения в ряд подынтегральной функции, и оценить допущенные при этом погрешности: 105. Ответы В задачах 1, 3, 6, 7, 8, 9, 10, 12, 13, 15, 17, 18, 19, 21, 22, 23, 31, 32, 33, 34, 35, 37, 38, 42, 43, 44 – ряды сходятся. В задачах 2, 4, 5, 11, 14, 16, 20, 24, 25, 26, 27, 28, 29, 30, 36, 39, 40, и 41 – ряды расходятся. В задачах 45, 46, 47, 49, 50, 51, 55 – ряды абсолютно сходятся. В задачах 48, 53, 54, 57 – ряды сходятся условно. В задачах 52, 56, 58, 59 – ряды расходятся. 60. (-1;1], 61. [-1/2;1/2), 62. {0}, 63. (-1/3;1/3], 64. (-1;1), 65. [0;2], 66. [-10;10), 67. (-∞;∞), 68. (-7;-1), 69. [-4;4), 70. (-2;2), 71. 86. 88. 90. 92. 94. 96. 98. 99. 102. 105.
Оглавление §1. Основные понятия. 4 §2. Признаки сходимости знакопостоянных рядов. 7 §3. Признаки сходимости знакопеременных рядов. 22 §4. Степенные ряды.. 27 §5. Ряды Маклорена и Тейлора. 32 §6. Применение рядов в приближенных вычислениях. 39 Ответы.. 43 Подписано в печать 2012 г. Формат 60´84/16. Бумага писчая. Отпечатано на ризографе. Уч. изд. листов 2.
Московский государственный университет тонких химических технологий им. М.В.Ломоносова Издательско-полиграфический центр 117571, Москва, просп. Вернадского, 86.
* Напомним, что степенью степенного выражения называется наибольшая из степеней входящих в него слагаемых, само это слагаемое называется старшим, а его коэффициент называется старшим коэффициентом. Например, у степенного выражения старшее слагаемое имеет степень 1,5, а старший коэффициент равен 5.
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.16.40 (0.007 с.) |


 ;
;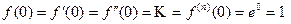 , и по формуле (5.2) получаем
, и по формуле (5.2) получаем . (5.3)
. (5.3) .
.
 ,
, 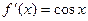 ,
, 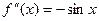 ,
,  ,
,  , откуда
, откуда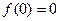 ,
,  ,
,  ,
,  ,
,  и т.д.
и т.д. , а нечетного порядка
, а нечетного порядка 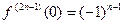 ,
,  , и по формуле (5.2) имеем
, и по формуле (5.2) имеем (5.4)
(5.4) .
.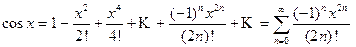 (5.5)
(5.5)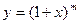 , где
, где  – любое действительное число.
– любое действительное число. ,
,  ,
, ,
,  , …,
, …, , …
, …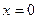 :
:  ,
,  ,
,  ,
, , …,
, …,  и по формуле (5.2) получаем
и по формуле (5.2) получаем (5.6)
(5.6) , исследуем с помощью признака Даламбера:
, исследуем с помощью признака Даламбера:
 .
. . На концах интервала при
. На концах интервала при 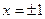 сходимость ряда зависит от конкретных значений
сходимость ряда зависит от конкретных значений  сомножитель
сомножитель  равен нулю, следовательно,
равен нулю, следовательно, 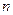 -йчлен ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма.
-йчлен ряда и все последующие равны нулю, т.е. ряд обрывается, и вместо бесконечного разложения получается конечная сумма. :
: ,
,  (5.7)
(5.7) вместо
вместо  , получим:
, получим: (5.8)
(5.8) :
: ,
,  :
: ,
,  .
. , где
, где  , с учетом того, что
, с учетом того, что  , получим
, получим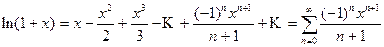 (5.11)
(5.11) .
.
 (5.12)
(5.12)
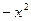 вместо
вместо 
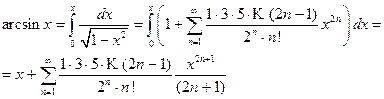 (5.13)
(5.13)


 , заменяя в разложении (5.5)
, заменяя в разложении (5.5)  :
:

 функцию
функцию 

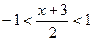 . Отсюда получаем
. Отсюда получаем  или
или  .
.
 запишем ряд (5.3) при
запишем ряд (5.3) при  , принадлежащем области сходимости
, принадлежащем области сходимости 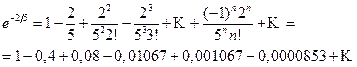
 , не превышающую первого отброшенного члена (по абсолютной величине), т.е.
, не превышающую первого отброшенного члена (по абсолютной величине), т.е.  .
.

 , входящее в область сходимости
, входящее в область сходимости 
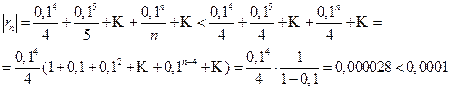 (здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна
(здесь мы учли, что сумма сходящегося геометрического ряда в скобках равна  )
)

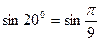 запишем ряд (5.4) при
запишем ряд (5.4) при  , принадлежащем области сходимости
, принадлежащем области сходимости 

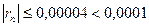 ). Итак,
). Итак, .
.
 , причем ряд сходится при всех значениях
, причем ряд сходится при всех значениях 

 .
.
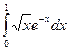
 в разложении (5.3), получим:
в разложении (5.3), получим: .
.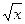 :
: ,
, , принадлежащем интервалу сходимости ряда
, принадлежащем интервалу сходимости ряда 



 . Итак,
. Итак,  .
. 87.
87. 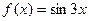 88.
88. 
 90.
90. 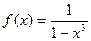 91.
91. 
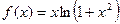
 по степеням
по степеням 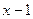
 по степеням
по степеням 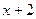
 по степеням
по степеням 
 по степеням
по степеням 
 по степеням
по степеням 
 по степеням
по степеням 
 100.
100.  101.
101.  102.
102. 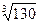 103.
103. 

 106.
106. 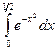
 , 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83.
, 72. [1;3), 73. (-1/3;1/3), 74. (-∞;∞), 75. [-1;1], 76. [-1;1), 77. (1;5], 78. (-1/4;1/4), 79. (-1/3;1/3), 80. (-3;1], 81. (-1;1], 82. (-∞;∞), 83.  , 84.
, 84.  , 85. [-1/ e;1/ e),
, 85. [-1/ e;1/ e), 87.
87. 
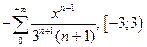 89.
89. 
 91.
91. 
 93.
93. 
 95.
95. 
 97.
97. 

 100.
100.  101.
101. 
 103.
103.  104.
104. 
 106.
106.  .
.


