
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Формула Тейлора для многочлена. Формула Тейлора для произвольной функции. Формула Маклорена.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Формула Тейлора для многочлена. Формула Тейлора для произвольной функции. Формула Маклорена. Если функция
и т.д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2:
ПРИМЕР 1. Разложение функции по формуле Тейлора в окрестности произвольной точки.
Аппроксимация функции многочленом. Выражение 32. Формула Маклорена для ех
Формула Маклорена для sinx
Формула Маклорена для cosx
35. Формула Маклорена для ln(1+x)
36. Формула Маклорена для (1+x)m
37. Понятие функции нескольких переменных. Область определения. Частные производные первого порядка и их геометрический смысл.
Величина z называется функцией переменных величин x и y на множестве D, если каждой точке этого множества соответствует одно определенное значение величины z. Множество точек D называется областью определения функции. Обычно областью определения функции является некоторая часть плоскости, ограниченная одной или несколькими линиями. Частными производными функции z = f (x,у) называются пределы отношения приращений функции z = z(х,у) к приращению соответствующего аргумента по направлениям ох или оу при Δх → 0 и Δу → 0 соответственно: Частная производная по х:
при вычислении считают у = const. Частная производная по у:
при вычислении считают x = const.
Геометрически
, где β – угол касательной к поверхности в точке с направлением оси оу. Полный дифференциал функции двух переменных и его применение к приближённым вычислениям. Дифференциал функции Функция z = f (M) дифференцируема в точке М, если ее полное приращение в этой точке может быть представлено в виде суммы линейной части относительно приращений аргументов и слагаемых более высокого порядка малости относительно приращений аргументов: Δ z = A Δ x + B Δ y + o (Δ x, Δ y) (1) где
Определение. Дифференциалом функции z = f (M) в точке М называется линейная относительно приращений аргументов Δ x и Δ у часть полного приращения этой функции в этой точке: d z = A ·Δ x + B ·Δ y. (2) Связь дифференциала с частными производными В выражении дифференциала (2) величины А и В равны частным производным функции по соответствующим переменным:
Доказательство. Зафиксируем переменную у, так что она не получает приращения Δ y = 0. В этом случае полное приращение функции Δ z становится частным по переменной х и формула (1) принимает вид Δx z = A ·Δ x + o (Δ x). Откуда
Переходя к пределу в обеих частях соотношения (3), получим
откуда, в силу определения частной производной
Из (4) следует, что дифференциалами независимых переменных х и у являются приращения этих переменных: dx = Δ x, dy = Δ y. Тогда дифференциал функции можно записать в виде
Из определения дифференциала следует, что разность между полным приращением и дифференциалом функции в точке М есть бесконечно малая более высокого порядка, чем Δ х и Δ у: Δ z - dz = o (Δ x, Δ y). Отбрасывая при достаточно малых Δ х и Δ у величину o (Δ x, Δ y), получаем приближенную формулу Δ z» dz, из которой вытекает формула линеаризации для функции многих переменных:
Касательная плоскость и нормаль к поверхности.
Формула Тейлора для многочлена. Формула Тейлора для произвольной функции. Формула Маклорена. Если функция
и т.д. Формула Тейлора, записанная в окрестности точки (0,0) называется формулой Маклорена. Например, для функции двух переменных при n=2:
ПРИМЕР 1. Разложение функции по формуле Тейлора в окрестности произвольной точки.
Аппроксимация функции многочленом. Выражение 32. Формула Маклорена для ех
Формула Маклорена для sinx
Формула Маклорена для cosx
35. Формула Маклорена для ln(1+x)
36. Формула Маклорена для (1+x)m
37. Понятие функции нескольких переменных. Область определения. Частные производные первого порядка и их геометрический смысл.
Величина z называется функцией переменных величин x и y на множестве D, если каждой точке этого множества соответствует одно определенное значение величины z. Множество точек D называется областью определения функции. Обычно областью определения функции является некоторая часть плоскости, ограниченная одной или несколькими линиями. Частными производными функции z = f (x,у) называются пределы отношения приращений функции z = z(х,у) к приращению соответствующего аргумента по направлениям ох или оу при Δх → 0 и Δу → 0 соответственно: Частная производная по х:
при вычислении считают у = const. Частная производная по у:
при вычислении считают x = const.
Геометрически
, где β – угол касательной к поверхности в точке с направлением оси оу.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 918; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.216.70.205 (0.01 с.) |

 имеет в некоторой окрестности точки
имеет в некоторой окрестности точки  непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки
непрерывные частные производные до (n+1)-го порядка включительно, то для любой точки 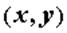 из этой окрестности справедлива формула Тейлора n-го порядка:
из этой окрестности справедлива формула Тейлора n-го порядка: 
 , где
, где  ,
,
 ,
,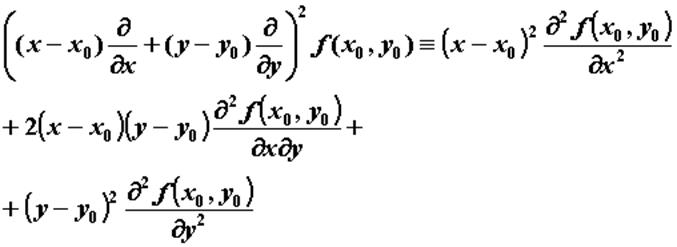
 .
.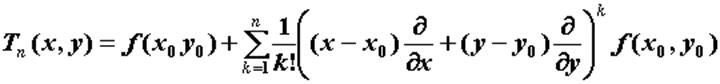 называется многочленом Тейлора n-го порядка. Поскольку
называется многочленом Тейлора n-го порядка. Поскольку  , то в окрестности точки функцию
, то в окрестности точки функцию  . Чем ближе точка
. Чем ближе точка 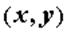 к точке
к точке  , тем точнее представляет ее многочлен Тейлора.
, тем точнее представляет ее многочлен Тейлора.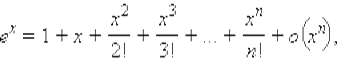



 где
где 
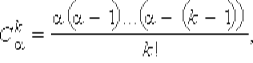


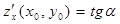


 .
. и
и  .
. . (3)
. (3) ,
,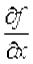 и определения бесконечно малой более высокого порядка, чем Δ х, получим
и определения бесконечно малой более высокого порядка, чем Δ х, получим  (4)
(4)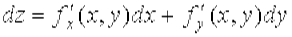 .
. .
.


