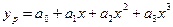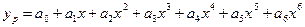Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Інтерполяційна формула ЛагранжаСодержание книги Поиск на нашем сайте
ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ Мета лабораторної роботи Здобуття практичних навичок у побудові інтерполяційних багаточленів Лагранжа і Ньютона та використанні їх для обчислення наближених значень функцій поза вузлами інтерполяції. Основні відомості Постановка задачі Для функцій, заданих таблицями їхніх значень на кінцевому інтервалі, виникає необхідність обчислення значень функцій для значень аргументів, відсутніх у таблиці. Тоді будують функцію, що у заданих точках приймає задані значення, а в інших точках інтервалу приблизно представляє задану функцію. А потім обчислення значень функції для будь-яких значень аргументу в області визначення таблично заданої функції виконують за побудованою функцією. Задача інтерполяції – побудова такої наближеної функції. Найчастіше інтерполяційну функцію знаходять у вигляді алгебраїчного багаточлену. Геометрично задача інтерполяції полягає в побудові кривої y=F (x), що проходить через таблично задану систему точок M 0(x 0, y 0), M 1(x 1, y 1), …, Mn (xn, yn). Інтерполяційна формула Лагранжа Нехай функція y=f (х) у точках x 0, x 1, ..., xn відповідно приймає значення y 0, y 1, ..., yn. Потрібно побудувати багаточлен Ln (x) ступеня не вище n, що приймає в точках x 0, x 1, ..., xn (вузлах інтерполяції) значення y 0, y 1, ..., yn. Відстань між вузлами інтерполяції може бути різною. Розв'язок цієї задачі – багаточлен Лагранжа
Інтерполяційну формулу Лагранжа можна записати в більш стислому вигляді:
де При цьому в точках x 0, x 1, …, xn значення багаточлену Ln (x) та функції f (x) збігаються. При інших значеннях x різниця Приклад 1.1. Задана функція
Побудувати інтерполяційний багаточлен Лагранжа й обчислити наближене значення функції для x =1,3. Розв'язок. Для побудови інтерполяційного багаточлену скористаємося формулою (1.1) при n =3:
Перевіряємо значення функції для вузлів інтерполяції: L 3(1,1) = 0,0648×1,13 – 0,5207×1,12 + 1,7981×1,1 – 1,3389 ≈ 0,0953; L 3(1,5) = 0,0648×1,53 – 0,5207×1,52 + 1,7981×1,5 – 1,3389 ≈ 0,4055;
L 3(2,0) = 0,0648×23 – 0,5207×22 + 1,7981×2 – 1,3389 ≈ 0,6931; L 3(2,6)= 0,0648×2,63 – 0,5207×2,62 + 1,7981×2,6 – 1,3389 ≈ 0,9555. Обчислюємо f (1,3)» L 3(1,3)» 0,2611. Відповідь: f (1,3) = 0,2611.
Інтерполяційну формулу в Excel можна побудувати досить простим способом. З практичної точки зору головна проблема полягає в обчисленні в довільній точці значень базисних функцій. Як приклад розглянемо задачу про побудову інтерполяційного полінома Лагранжа за даними Прикладу 1.1.
На рис. 1.1 представлені вихідні дані, за якими буде виконуватися інтерполяція. На цьому ж рисунку проілюстрований процес визначення першої базисної функції. Рис.1.1
У діапазоні комірок А6:А9 представлені задані значення аргументів функції, а в діапазоні комірок В6:В9 – значення функції для вузлових точок аргументу. В комірку А2 вводиться значення аргументу, для якого необхідно обчислити значення інтерполяційного полінома. Значення полінома буде виводитися в комірку В2. Важливим моментом є заповнення комірок у діапазоні С6:С9, де будуть відображатися значення базисних функцій у точці, що зазначена вкомірці А2. Саме за цими значеннями і значенням комірок з діапазону А6:А9 визначається значення інтерполяційного полінома (комірка В2). Діапазон С6:С9 заповнюється так: окремо перша і остання комірки діапазону, а всі інші комірки – поширенням однієї формули. Зокрема, в комірку С6 вводиться формула =ПРОИЗВЕД(A2-A7:A9)/ПРОИЗВЕД(A6-A7:A9),відповідно до якої визначається перша базисна функція. Відразу слід зазначити, що й ця формула, і всі інші формули з діапазону С6:С9, вводяться як формули для діапазонів, тобто за допомогою натискання комбінації клавіш Ctrl+Shift+Enter. Причина полягає в тому, що аргументами функції ПРОИЗВЕД()вказуються результати арифметичних операцій з діапазонами. Далі заповнюються комірки з діапазону С7: С8. Для цього в комірку С7 вводиться формула =ПРОИЗВЕД($A$2-$A$6:A6;$A$2-A8:$A$9)/ ПРОИЗВЕД(A7-$A$6:A6;A7-A8:$A$9). Абсолютні й відносні посилання у формулі підібрані так, щоб при її копіюванні в наступні комірки, посилання на початкову С6 і кінцеву С9 комірки діапазону, так само як і на комірку А2 зі значенням змінної, для якої обчислюється базисна функція (і весь поліном), залишалися незмінними. Це абсолютні посилання. Разом з тим, в процесі копіювання формули добутку в ній обчислюються без урахування значення аргументу в тому рядку, де розміщена формула. Після введення формули в комірку С7 дана формула за допомогою маркеру заповнення копіюється в усі комірки, аж до С8.
Нарешті, в комірку С9 необхідно ввести формулу =ПРОИЗВЕД(А2-А6:А8)/ ПРОИЗВЕД(А9-А6:А8). Оскільки формули з початкової С6 і кінцевої С9 комірок діапазону С6:С9 нікуди копіювати не передбачається, то й посилання там відносні. Результат можна бачити на рис. 1.2. Рис. 1.2 Після цього залишилося обчислити значення інтерполяційного полінома. Для цього досить в комірку В2 ввести формулу =СУММПРОИЗВ(B6:B9;C6:C9). Ця формула вводиться як звичайна, тобто потрібно натиснути клавішу Enter. Результат представлений на рис. 1.3.
Рис.1.3 Для розрахунку значення полінома в якійсь точці, відповідне значення варто ввести в комірку А2. В комірці В2 практично відразу з'явиться результат. Відповідь: f (1,3) = 0,2611.
На рис. 1.4 проілюстрована ситуація, коли в якості аргументу зазначене вузлове значення. Як і слід було сподіватися, у вузловій точці значення інтерполяційного полінома дорівнює експериментальному значенню функції в цій точці, а всі базисні функції, крім тієї, що відповідає зазначеному вузлу, дорівнюють нулю. Відмінна від нуля базисна функція дорівнює одиниці. Рис.1.4
Використання Excel для розв'язання задач цього класу є досить ефективним і розкриває широкі обрії перед кожним дослідником. Запропонований спосіб побудови інтерполяційного полінома, безумовно, не єдиний. Крім того, поліном зовсім не обов'язково знаходити саме у формі Лагранжа. Тому вибір методу, типу інтерполяційного полінома і вирішення інших подібних питань здійснюється, як правило, у контексті конкретної задачі. Питання для самоперевірки 1. Коли виникає необхідність побудови інтерполяційних функцій? 2. Що таке вузол інтерполяції? 3. Поясніть поняття «інтерполяційна функція». 4. Як будується інтерполяційний багаточлен Лагранжа? 5. Яка сутність поняття «скінченна різниця»? 6. Як обчислюються скінченні різниці першого, другого й n -го порядків? 7. Що таке перша інтерполяційна формула Ньютона? 8. Чим відрізняється друга інтерполяційна формула Ньютона від першої? 9. У чому полягає перевага інтерполяційних багаточленів Ньютона перед інтерполяційним багаточленом Лагранжа? 10. Який недолік інтерполяційних багаточленів Ньютона? 11. Як визначити похибку інтерполяційних формул Ньютона? 12. Наведіть схему алгоритму обчислення значення функції за інтерполяційним багаточленом Лагранжа. 13. Наведіть схему алгоритму обчислення значення функції за першою інтерполяційною формулою Ньютона. 14. Наведіть схему алгоритму обчислення значення функції за другою інтерполяційною формулою Ньютона. Мета лабораторної роботи Здобуття практичних навичок побудови апроксимуючих функцій (аналітичних залежностей) за сукупністю дискретних експериментальних даних. Основні відомості Постановка задачі В інженерній практиці у процесі пошуку закономірностей протікання явищ і процесів виникає задача визначення за даними спостережень аналітичних залежностей одного параметра від іншого. Загальна постановка цієї задачі може мати такий вигляд. Відомо, що між х і у існує функціональна залежність. У результаті експерименту отримана таблиця значень
Потрібно знайти функцію, що наближено описує зв'язок між х і у. Експериментальними даними у такій задачі є табличне представлення функції, яку потрібно апроксимувати деякою аналітичною функцією. Рівняння такої функції є рівнянням зв'язку, що називають також рівнянням регресії. Регресійний аналіз полягає у визначенні аналітичного вираження зв'язку, у якому зміна однієї величини обумовлена впливом одного або декількох незалежних факторів. Регресія може бути однофакторною і багатофакторною. За формою залежності розрізняють: · лінійна регресія; · нелінійна регресія, яка виражається рівняннями степеневої, показникової, експоненційної функцій, а також рівняннями гіперболи і параболи. Побудова формули включає два етапи: · з'ясування загального виду залежності; · визначення найкращих параметрів залежності. Підбір рівняння регресії у значній мірі залежить від досвіду й мистецтва дослідника. При достатньому досвіді за геометричним розташуванням експериментальних даних можна з достатньою точністю визначити вид апроксимуючої функції. У багатьох випадках вибирається (коли немає інших явних ознак) поліном виду у= а 0 + а 1 х +...+ аmхm. Однак, який би не був вид апроксимуючої функції, виникає задача визначення таких її параметрів, які б найкращим чином узгоджувалися з експериментальними даними. Одним з таких ефективних методів є метод найменших квадратів. Метод найменших квадратів Сутність даного методу полягає в тому, що є залежність f (x, a 0, a 1,..., am), близька до заданої сукупності значень xi , yi у змісті мінімуму квадратичного відхилення
де e i – відхилення апроксимуючої функції від експериментальних значень e i= f (xi, a 0, a 1,..., am)– yi, i= 0, 1, 2, ..., n. (2.2) Тоді задача полягає у виборі такої сукупності параметрів a 0, a 1,..., am, при яких значення критерію (2.1) є мінімальним. При цьому завжди n>m, тому що у випадку n=m виходить задача інтерполяції, в якій значення критерію R може бути зведено до нуля. Необхідною умовою мінімуму критерію (2.1) є рівність нулю всіх частинних похідних функції R по a 0, a 1,..., am, тобто
Вирішуючи систему рівнянь (2.3), знаходимо значення a 0, a 1,..., am коефіцієнтів шуканої залежності. Лінійна регресія Нехай шукана функція є лінійної відносно х, тобто у=а 0 +а 1 x. Тоді критерій (2.1) прийме вигляд:
Умови мінімуму цього критерію:
Система рівнянь (2.5), одержуваних диференціюванням (2.4), прийме вигляд:
Або після перетворень
Звідки
Знайдені значення а 0 і а 1 підставляються в шукане рівняння у=а 0 +а 1 x. Поліноміальна регресія Якщо лінійна апроксимуюча функція дає в заданих точках значні відхилення, використовується наближення поліномами другого і вище ступенів вигляду
Так, для квадратних наближень (при m = 2) визначення параметрів a 0, a 1, a 2 за методом найменших квадратів зводиться до знаходження мінімуму критерію (2.1) як функції трьох змінних a 0, a 1, a 2:
Умови мінімуму квадратичного критерію мають вигляд:
або після перетворень:
Обчислення коефіцієнтів систем (2.7) зручно виконувати у вигляді табл. 2.1. Таблиця 2.1
Визначення параметрів нелінійних апроксимуючих функцій методом найменших квадратів пов'язане із трудомістким розв'язанням систем нелінійних рівнянь. Таблиця 2.2
Для знаходження коефіцієнтів a 0 і a 1 складається система
Звідки a 0 =0,766; a 1 = – 0,177. Відповідь: апроксимуюча функція f 1(x, a 0, a 1) = 0,766 – 0,177 x. Для знаходження коефіцієнтів a 0, a 1, a 2 багаточлена другого ступеня одержимо за (2.7)
Звідки a 0 = – 0,458; a 1 = – 0,454; a 2 = 0,256. Відповідь: апроксимуюча функція f 2(x, a 0, a 1, a 2)= – 0,458 – 0,454 x + 0,256 х 2.
Побудуємо отримані залежності (рис. 2.1) і позначимо задані точки. Рис. 2.1 Обчислимо за (2.2) відхилення апроксимуючих залежностей. Оформимо обчислення у вигляді табл. 2.3. Таблиця 2.3
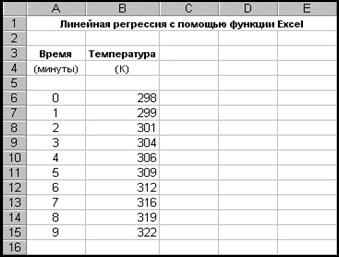
Звідси Виконання регресії в Excel Приклад 2.2. Як приклад проаналізуємо простий набір даних, що включає в себе значення температури й часу (рис. 2.2). Цей приклад дозволяє ознайомитися з основними прийомами проведення регресійного аналізу в Excel. Крок 1. Введення вихідних даних. Будь-які вихідні дані можуть бути введені в необхідні комірки вручну. Якщо в серії чисел, що вводяться, є закономірність, то зручніше вводити їх за допомогою допоміжного інструмента, прискорюючого роботу, – заповнювача. Опція Заполнить в меню Правка постійно готова до роботи. Вона відкриває діалогове вікно, що надає великий вибір можливостей для заповнення серій даних за стовпцями або за рядками. За допомогою такого заповнювача легко створювати ряди.
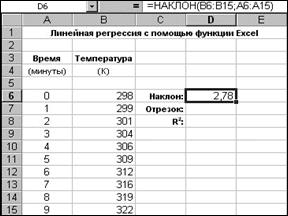
Для визначення кутового коефіцієнта прямої лінії, що найкраще описує дані, призначена функція НАКЛОН(). У функції НАКЛОН() два аргументи, розташовані в такому порядку: діапазон комірок, що містить значення y (значення залежної змінної), і діапазон комірок, що містять значення x (значення незалежної змінної) (рис. 2.3). У цьому випадку вивчається залежність температури від часу, а не навпаки, тому залежною змінною є температура (комірки B6:B15), а час (комірки A6:A15) вважається незалежною змінною.
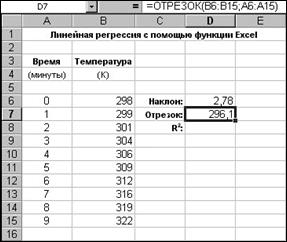
Рис. 2.3 Аналогічно, точку перетину прямої регресії з віссю ординат можна знайти за допомогою функції ОТРЕЗОК() з тими ж аргументами (рис. 2.4).
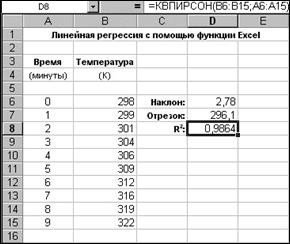
Рис. 2.4 Квадрат коефіцієнту кореляції (R2) обчислюється за допомогою функції КВПИРСОН() з тими ж аргументами, що й у попередніх функцій (рис. 2.5).
Рис. 2.5 Отримані результати свідчать про те, що пряма, яка найкраще описує дані, має кутовий коефіцієнт a 1 = 2,7758 К/хв і перетинає вісь ординат у точці a 0 = 296,1 К. Значення R 2 дорівнює 0,9864. Таким чином, обчислений кутовий коефіцієнт, знайдена точка перетину лінії регресії з віссю ординат, а також величина R 2. Наскільки добре пряма лінія описує дані? Щоб відповісти на це питання, можна побудувати діаграму з даними й лінією регресії, що дозволяє візуально переконатися в ступені їхнього збігу. Рис. 2.13 Результат апроксимації даних виглядає ненабагато краще попередньої апроксимації, і відповідна їй величина R 2 майже така ж, яка була отримана при використанні рівняння прямої як моделі регресії. На вкладці Тип діалогового вікна Формат линии тренда є ще один варіант вибору – Полиномиальная. Поліноміальна регресія Поліноміальна регресія теж лінійна, оскільки поліноміальні коефіцієнти (ai) входять у рівняння регресії лінійно. Вона відрізняється від інших моделей регресії тим, що містить у собі більше двох коефіцієнтів. Формально регресія за допомогою рівняння прямої також є поліноміальною регресією, однак цей термін звичайно застосовується для поліномів другого ступеня або вище. У програмі Excel можна побудувати лінії тренда, ступінь яких знаходиться в межах від 2 до 6 (табл. 2.5). Таблиця 2.5
Примітка. Загально прийнято записувати поліноми, розміщуючи ступені зліва направо у порядку зростання. Однак в Excel рівняння поліноміальної лінії тренда записуються у зворотному порядку, на що варто звернути увагу при читанні рівнянь.
Щоб побудувати поліноміальну регресію другого порядку, відобразіть на екрані діалогове вікно Формат линии тренда, двічі натиснувши на існуючій лінії тренда (рис. 2.14). Рис. 2.14 Оберіть тип Полиномиальная і встановіть Степень, рівну 2 (рис.2.15).
Рис. 2.15 Схоже, поліноміальна лінія тренда описує дані краще лінійної, і відповідна їй величина R 2 близька до одиниці. За допомогою ліній тренда регресія виконується досить легко й швидко. Однак що робити, якщо в програмі Excel необхідно апроксимувати дані поліноміальній кривій сьомого ступеня? Таку регресію дозволяє виконати спеціальний пакет аналізу, доступ до якого здійснюється за допомогою команди меню Сервис ® Анализ данных... ® Регрессия. Виконання лінійної регресії за допомогою пакету регресійного аналізу трохи складніше, ніж звичайна побудова лінії тренда на діаграмі. Такий більш складний підхід може знадобитися ще з двох причин. 1. Необхідність використання моделі регресії, лінія тренда якої відсутня. 2. Потреба в більш докладній інформації про процес регресії, яку не можна одержати за допомогою ліній тренда. Один з видів інформації – графік залишків, що дозволяє виявити погані збіги й полегшує їхнє виявлення, – можна витягти, скориставшись винятково пакетом регресійного аналізу. Виконання лінійної регресії за допомогою пакета регресійного аналізу буде розглянуто в окремій лабораторній роботі. Будь-яке регресійне рівняння – це спрощення реальності, змушена «відмова» від реально діючих факторів, їхнє відсікання. Тому кінцевий результат формального моделювання завжди повинен оцінюватися користувачем з погляду здорового глузду на основі неформального комплексу знань про умови розвитку процесу й про припустимі граничні значення показника. На одному наборі вихідних даних можна одержати до дев'яти рівнянь трендів. Задача дослідника полягає у відборі найкращого тренда, за яким можна було б побудувати надійний прогноз. Фахівець, який розуміє умови розвитку процесу і має досвід моделювання трендів, можливо, не стане перебирати всі альтернативні типи, добре знаючи традиційні залежності, характерні для конкретних показників. У противному випадку необхідно досліджувати всі типи для пошуку рівняння з найвищим значенням коефіцієнта детермінації (R 2). Питання для самоперевірки 1. Яка загальна постановка задачі апроксимації? 2. У чому відмінність задачі апроксимації від задачі інтерполяції? 3. З яких етапів складається побудова регресійної формули? 4. У чому суть методу найменших квадратів? 5. Як обчислюється відхилення апроксимуючої функції від експериментальних значень? 6. Що є умовою мінімуму критерію квадратичного відхилення? 7. Як одержати систему рівнянь для визначення коефіцієнтів апроксимуючої функції за методом найменших квадратів? 8. Назвіть приклади апроксимуючих функцій і їхні лінійні аналоги. 9. Що таке тренд? У чому складається його сутність? 10. Який вид моделей потрібен, якщо необхідно не тільки прогнозувати майбутні значення показників, але й управляти їхніми змінами? 11. Перелічить основні типи трендів. Які з них підтримує Ехсеl? 12. Запишіть формулу тренда кожноготипу. 13. Які засоби Ехсеl належать до основних засобів побудови трендів? 14. На якому типі діаграм моделюються тренди? 15. Перелічить в технологічній послідовності етапи побудови ліній трендів. Додаток 1 ІНТЕРПОЛЯЦІЯ ФУНКЦІЙ Мета лабораторної роботи Здобуття практичних навичок у побудові інтерполяційних багаточленів Лагранжа і Ньютона та використанні їх для обчислення наближених значень функцій поза вузлами інтерполяції. Основні відомості Постановка задачі Для функцій, заданих таблицями їхніх значень на кінцевому інтервалі, виникає необхідність обчислення значень функцій для значень аргументів, відсутніх у таблиці. Тоді будують функцію, що у заданих точках приймає задані значення, а в інших точках інтервалу приблизно представляє задану функцію. А потім обчислення значень функції для будь-яких значень аргументу в області визначення таблично заданої функції виконують за побудованою функцією. Задача інтерполяції – побудова такої наближеної функції. Найчастіше інтерполяційну функцію знаходять у вигляді алгебраїчного багаточлену. Геометрично задача інтерполяції полягає в побудові кривої y=F (x), що проходить через таблично задану систему точок M 0(x 0, y 0), M 1(x 1, y 1), …, Mn (xn, yn). Інтерполяційна формула Лагранжа Нехай функція y=f (х) у точках x 0, x 1, ..., xn відповідно приймає значення y 0, y 1, ..., yn. Потрібно побудувати багаточлен Ln (x) ступеня не вище n, що приймає в точках x 0, x 1, ..., xn (вузлах інтерполяції) значення y 0, y 1, ..., yn. Відстань між вузлами інтерполяції може бути різною. Розв'язок цієї задачі – багаточлен Лагранжа
Інтерполяційну формулу Лагранжа можна записати в більш стислому вигляді:
де При цьому в точках x 0, x 1, …, xn значення багаточлену Ln (x) та функції f (x) збігаються. При інших значеннях x різниця Приклад 1.1. Задана функція
Побудувати інтерполяційний багаточлен Лагранжа й обчислити наближене значення функції для x =1,3. Розв'язок. Для побудови інтерполяційного багаточлену скористаємося формулою (1.1) при n =3:
Перевіряємо значення функції для вузлів інтерполяції: L 3(1,1) = 0,0648×1,13 – 0,5207×1,12 + 1,7981×1,1 – 1,3389 ≈ 0,0953; L 3(1,5) = 0,0648×1,53 – 0,5207×1,52 + 1,7981×1,5 – 1,3389 ≈ 0,4055; L 3(2,0) = 0,0648×23 – 0,5207×22 + 1,7981×2 – 1,3389 ≈ 0,6931; L 3(2,6)= 0,0648×2,63 – 0,5207×2,62 + 1,7981×2,6 – 1,3389 ≈ 0,9555. Обчислюємо f (1,3)» L 3(1,3)» 0,2611. Відповідь: f (1,3) = 0,2611.
Інтерполяційну формулу в Excel можна побудувати досить простим способом. З практичної точки зору головна проблема полягає в обчисленні в довільній точці значень базисних функцій. Як приклад розглянемо задачу про побудову інтерполяційного полінома Лагранжа за даними Прикладу 1.1.
На рис. 1.1 представлені вихідні дані, за якими буде виконуватися інтерполяція. На цьому ж рисунку проілюстрований процес визначення першої базисної функції. Рис.1.1
У діапазоні комірок А6:А9 представлені задані значення аргументів функції, а в діапазоні комірок В6:В9 – значення функції для вузлових точок аргументу. В комірку А2 вводиться значення аргументу, для якого необхідно обчислити значення інтерполяційного полінома. Значення полінома буде виводитися в комірку В2. Важливим моментом є заповнення комірок у діапазоні С6:С9, де будуть відображатися значення базисних функцій у точці, що зазначена вкомірці А2. Саме за цими значеннями і значенням комірок з діапазону А6:А9 визначається значення інтерполяційного полінома (комірка В2). Діапазон С6:С9 заповнюється так: окремо перша і остання комірки діапазону, а всі інші комірки – поширенням однієї формули. Зокрема, в комірку С6 вводиться формула =ПРОИЗВЕД(A2-A7:A9)/ПРОИЗВЕД(A6-A7:A9),відповідно до якої визначається перша базисна функція. Відразу слід зазначити, що й ця формула, і всі інші формули з діапазону С6:С9, вводяться як формули для діапазонів, тобто за допомогою натискання комбінації клавіш Ctrl+Shift+Enter. Причина полягає в тому, що аргументами функції ПРОИЗВЕД()вказуються результати арифметичних операцій з діапазонами. Далі заповнюються комірки з діапазону С7: С8. Для цього в комірку С7 вводиться формула =ПРОИЗВЕД($A$2-$A$6:A6;$A$2-A8:$A$9)/ ПРОИЗВЕД(A7-$A$6:A6;A7-A8:$A$9). Абсолютні й відносні посилання у формулі підібрані так, щоб при її копіюванні в наступні комірки, посилання на початкову С6 і кінцеву С9 комірки діапазону, так само як і на комірку А2 зі значенням змінної, для якої обчислюється базисна функція (і весь поліном), залишалися незмінними. Це абсолютні посилання. Разом з тим, в процесі копіювання формули добутку в ній обчислюються без урахування значення аргументу в тому рядку, де розміщена формула. Після введення формули в комірку С7 дана формула за допомогою маркеру заповнення копіюється в усі комірки, аж до С8.
Нарешті, в комірку С9 необхідно ввести формулу =ПРОИЗВЕД(А2-А6:А8)/ ПРОИЗВЕД(А9-А6:А8). Оскільки формули з початкової С6 і кінцевої С9 комірок діапазону С6:С9 нікуди копіювати не передбачається, то й посилання там відносні. Результат можна бачити на рис. 1.2. Рис. 1.2 Після цього залишилося обчислити значення інтерполяційного полінома. Для цього досить в комірку В2 ввести формулу =СУММПРОИЗВ(B6:B9;C6:C9). Ця формула вводиться як звичайна, тобто потрібно натиснути клавішу Enter. Результат представлений на рис. 1.3.
Рис.1.3 Для розрахунку значення полінома в якійсь точці, відповідне значення варто ввести в комірку А2. В комірці В2 практично відразу з'явиться результат. Відповідь: f (1,3) = 0,2611.
На рис. 1.4 проілюстрована ситуація, коли в якості аргументу зазначене вузлове значення. Як і слід було сподіватися, у вузловій точці значення інтерполяційного полінома дорівнює експериментальному значенню функції в цій точці, а всі базисні функції, крім тієї, що відповідає зазначеному вузлу, дорівнюють нулю. Відмінна від нуля базисна функція дорівнює одиниці. Рис.1.4
Використання Excel для розв'язання задач цього класу є досить ефективним і розкриває широкі обрії перед кожним дослідником. Запропонований спосіб побудови інтерполяційного полінома, безумовно, не єдиний. Крім того, поліном зовсім не обов'язково знаходити саме у формі Лагранжа. Тому вибір методу, типу інтерполяційного полінома і вирішення інших подібних питань здійснюється, як правило, у контексті конкретної задачі.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 992; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.214.156 (0.013 с.) |

 .(1.1)
.(1.1) , (1.2)
, (1.2)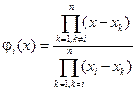 – так звані базисні функції, чисельник яких містить всі різниці (x–xk), а знаменник – всі різниці за винятком (xk–xk).
– так звані базисні функції, чисельник яких містить всі різниці (x–xk), а знаменник – всі різниці за винятком (xk–xk). в загальному випадку відмінна від нуля і являє собою істинну похибку методу. Величина Rn (х)є залишковим членом інтерполяції.
в загальному випадку відмінна від нуля і являє собою істинну похибку методу. Величина Rn (х)є залишковим членом інтерполяції.




 , (2.1)
, (2.1) . (2.3)
. (2.3) (2.4)
(2.4)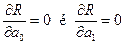 . (2.5)
. (2.5)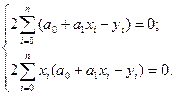

 (2.6)
(2.6)
 .
.
 (2.7)
(2.7)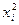
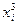
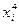













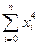


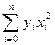
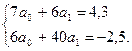

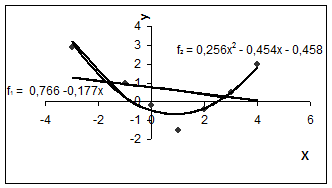
 .
.