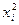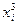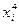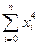Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Порядок виконання індивідуального завданняСодержание книги Поиск на нашем сайте
1. Відповідно до порядкового номера прізвища студента в журналі групи виписати з табл. 1 Додатку 1 значення аргументів і відповідні їм значення функції. 2. Побудувати інтерполяційний багаточлен Лагранжа. 3. Перевірити значення функції для вузлів інтерполяції. 4. Обчислити за інтерполяційною формулою Лагранжа значення функції для значення аргументу х 1, зазначеного в 12-му стовпці таблиці завдань (див. Приклад 1.1). 5. Скласти таблицю скінченних різниць для таблично заданої функції. 6. Обчислити за першою інтерполяційною формулою Ньютона значення функції для значення аргументу х 3, зазначеного в 14-му стовпці таблиці завдань. Оформити обчислення у вигляді таблиці (див. Приклад 1.2). 7. Обчислити за другою інтерполяційною формулою Ньютона значення функції для значення аргументу х 2, зазначеного в 13-му стовпці таблиці завдань. Оформити обчислення у вигляді таблиці (див. Приклад 1.2). 8. Виконати обчислення за допомогою Excel. 9. Порівняти результати обчислень «вручну» і на комп'ютері. 10. Оформити звіт. 11. Захистити звіт. Оформлений звіт представити на підпис викладачеві, що веде заняття. Необхідно вміти пояснити зміст звіту, а також відповісти на теоретичні питання з суті лабораторної роботи.
ЛАБОРАТОРНА РОБОТА №2 АПРОКСИМАЦІЯ. МЕТОД НАЙМЕНШИХ КВАДРАТІВ Мета лабораторної роботи Здобуття практичних навичок побудови апроксимуючих функцій (аналітичних залежностей) за сукупністю дискретних експериментальних даних. Основні відомості Постановка задачі В інженерній практиці у процесі пошуку закономірностей протікання явищ і процесів виникає задача визначення за даними спостережень аналітичних залежностей одного параметра від іншого. Загальна постановка цієї задачі може мати такий вигляд. Відомо, що між х і у існує функціональна залежність. У результаті експерименту отримана таблиця значень
Потрібно знайти функцію, що наближено описує зв'язок між х і у. Експериментальними даними у такій задачі є табличне представлення функції, яку потрібно апроксимувати деякою аналітичною функцією. Рівняння такої функції є рівнянням зв'язку, що називають також рівнянням регресії. Регресійний аналіз полягає у визначенні аналітичного вираження зв'язку, у якому зміна однієї величини обумовлена впливом одного або декількох незалежних факторів. Регресія може бути однофакторною і багатофакторною. За формою залежності розрізняють: · лінійна регресія; · нелінійна регресія, яка виражається рівняннями степеневої, показникової, експоненційної функцій, а також рівняннями гіперболи і параболи. Побудова формули включає два етапи: · з'ясування загального виду залежності; · визначення найкращих параметрів залежності. Підбір рівняння регресії у значній мірі залежить від досвіду й мистецтва дослідника. При достатньому досвіді за геометричним розташуванням експериментальних даних можна з достатньою точністю визначити вид апроксимуючої функції. У багатьох випадках вибирається (коли немає інших явних ознак) поліном виду у= а 0 + а 1 х +...+ аmхm. Однак, який би не був вид апроксимуючої функції, виникає задача визначення таких її параметрів, які б найкращим чином узгоджувалися з експериментальними даними. Одним з таких ефективних методів є метод найменших квадратів. Метод найменших квадратів Сутність даного методу полягає в тому, що є залежність f (x, a 0, a 1,..., am), близька до заданої сукупності значень xi , yi у змісті мінімуму квадратичного відхилення
де e i – відхилення апроксимуючої функції від експериментальних значень e i= f (xi, a 0, a 1,..., am)– yi, i= 0, 1, 2, ..., n. (2.2) Тоді задача полягає у виборі такої сукупності параметрів a 0, a 1,..., am, при яких значення критерію (2.1) є мінімальним. При цьому завжди n>m, тому що у випадку n=m виходить задача інтерполяції, в якій значення критерію R може бути зведено до нуля. Необхідною умовою мінімуму критерію (2.1) є рівність нулю всіх частинних похідних функції R по a 0, a 1,..., am, тобто
Вирішуючи систему рівнянь (2.3), знаходимо значення a 0, a 1,..., am коефіцієнтів шуканої залежності. Лінійна регресія Нехай шукана функція є лінійної відносно х, тобто у=а 0 +а 1 x. Тоді критерій (2.1) прийме вигляд:
Умови мінімуму цього критерію:
Система рівнянь (2.5), одержуваних диференціюванням (2.4), прийме вигляд:
Або після перетворень
Звідки
Знайдені значення а 0 і а 1 підставляються в шукане рівняння у=а 0 +а 1 x. Поліноміальна регресія Якщо лінійна апроксимуюча функція дає в заданих точках значні відхилення, використовується наближення поліномами другого і вище ступенів вигляду
Так, для квадратних наближень (при m = 2) визначення параметрів a 0, a 1, a 2 за методом найменших квадратів зводиться до знаходження мінімуму критерію (2.1) як функції трьох змінних a 0, a 1, a 2:
Умови мінімуму квадратичного критерію мають вигляд:
або після перетворень:
Обчислення коефіцієнтів систем (2.7) зручно виконувати у вигляді табл. 2.1. Таблиця 2.1
Визначення параметрів нелінійних апроксимуючих функцій методом найменших квадратів пов'язане із трудомістким розв'язанням систем нелінійних рівнянь.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 219; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.169.169 (0.007 с.) |

 , (2.1)
, (2.1) . (2.3)
. (2.3) (2.4)
(2.4)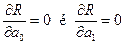 . (2.5)
. (2.5)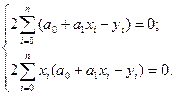

 (2.6)
(2.6)
 .
.
 (2.7)
(2.7)