Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приклад виконання апроксимації поліномамиСодержание книги Поиск на нашем сайте Якщо є набір експериментальних точок з (n +1) точок, то порядок апроксимуючого полінома завжди повинен бути менший, ніж кількість цих точок (m < n). Зі зменшенням m емпірична залежність спрощується, але похибка апроксимації зростає. Завищення m приводить до невиправданого росту числа обчислювальних операцій. При виборі ступеня полінома зручно користуватися таблицею скінченних різниць. Ступінь полінома можна брати рівним порядку скінченних різниць, що мало відрізняються. Лінійна апроксимація придатна тільки тоді, коли перші скінченні різниці мало відрізняються одна від одної. Для перевірки відповідності рівняння регресії експериментальним даним обчислюють похибку апроксимації (2.2). Якщо відхилення за модулем не перевищують похибки вимірів функції, то можна вважати виведену формулу прийнятною. У противному випадку рекомендується змінити ступінь полінома або змінити вид шуканої формули. Приклад 2.1. Функція задана таблично:
Знайти багаточлени першого й другого ступеня, що апроксимують задану функцію. Розв'язок. Обчислення коефіцієнтів (2.6) і (2.7) оформимо у вигляді табл. 2.2. Таблиця 2.2
Для знаходження коефіцієнтів a 0 і a 1 складається система
Звідки a 0 =0,766; a 1 = – 0,177. Відповідь: апроксимуюча функція f 1(x, a 0, a 1) = 0,766 – 0,177 x. Для знаходження коефіцієнтів a 0, a 1, a 2 багаточлена другого ступеня одержимо за (2.7)
Звідки a 0 = – 0,458; a 1 = – 0,454; a 2 = 0,256. Відповідь: апроксимуюча функція f 2(x, a 0, a 1, a 2)= – 0,458 – 0,454 x + 0,256 х 2.
Побудуємо отримані залежності (рис. 2.1) і позначимо задані точки. Рис. 2.1 Обчислимо за (2.2) відхилення апроксимуючих залежностей. Оформимо обчислення у вигляді табл. 2.3. Таблиця 2.3
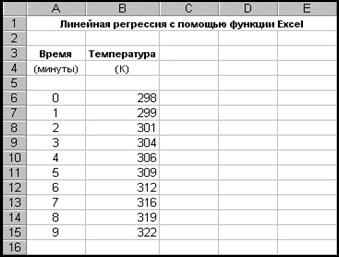
Звідси Виконання регресії в Excel Виконання лінійної регресії за допомогою функцій Excel У тому випадку, коли потрібно обчислити кутовий коефіцієнт a 1 і знайти точку перетину з віссю ординат прямої лінії a 0 дуже корисними виявляться функції Excel НАКЛОН() і ОТРЕЗОК(). Додавши до них функцію КВПИРСОН(), що обчислює квадрат коефіцієнта кореляції, одержимо найпростіший набір, що дозволяє вирішити задачу аналізу даних. Приклад 2.2. Як приклад проаналізуємо простий набір даних, що включає в себе значення температури й часу (рис. 2.2). Цей приклад дозволяє ознайомитися з основними прийомами проведення регресійного аналізу в Excel. Крок 1. Введення вихідних даних. Будь-які вихідні дані можуть бути введені в необхідні комірки вручну. Якщо в серії чисел, що вводяться, є закономірність, то зручніше вводити їх за допомогою допоміжного інструмента, прискорюючого роботу, – заповнювача. Опція Заполнить в меню Правка постійно готова до роботи. Вона відкриває діалогове вікно, що надає великий вибір можливостей для заповнення серій даних за стовпцями або за рядками. За допомогою такого заповнювача легко створювати ряди.
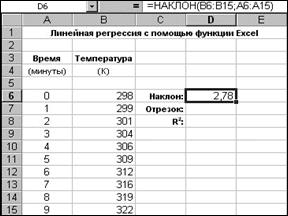
Для визначення кутового коефіцієнта прямої лінії, що найкраще описує дані, призначена функція НАКЛОН(). У функції НАКЛОН() два аргументи, розташовані в такому порядку: діапазон комірок, що містить значення y (значення залежної змінної), і діапазон комірок, що містять значення x (значення незалежної змінної) (рис. 2.3). У цьому випадку вивчається залежність температури від часу, а не навпаки, тому залежною змінною є температура (комірки B6:B15), а час (комірки A6:A15) вважається незалежною змінною.
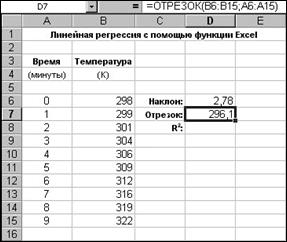
Рис. 2.3 Аналогічно, точку перетину прямої регресії з віссю ординат можна знайти за допомогою функції ОТРЕЗОК() з тими ж аргументами (рис. 2.4).
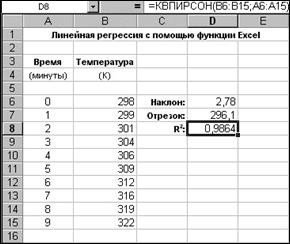
Рис. 2.4 Квадрат коефіцієнту кореляції (R2) обчислюється за допомогою функції КВПИРСОН() з тими ж аргументами, що й у попередніх функцій (рис. 2.5).
Рис. 2.5 Отримані результати свідчать про те, що пряма, яка найкраще описує дані, має кутовий коефіцієнт a 1 = 2,7758 К/хв і перетинає вісь ординат у точці a 0 = 296,1 К. Значення R 2 дорівнює 0,9864. Таким чином, обчислений кутовий коефіцієнт, знайдена точка перетину лінії регресії з віссю ординат, а також величина R 2. Наскільки добре пряма лінія описує дані? Щоб відповісти на це питання, можна побудувати діаграму з даними й лінією регресії, що дозволяє візуально переконатися в ступені їхнього збігу.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 356; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.009 с.) |

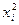
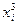
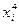
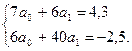

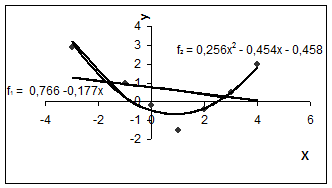
 .
.