
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Связь производной по направлению с частными производнымиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Предположим теперь, что функция f (М) дифференцируема в точке М. Приращение функции f (М) в точке М вдоль прямой l можно записать в виде
где
получим
Переходя к пределу в этом равенстве при Δ l → 0, получаем формулу для производной по направлению
Из этой формулы следует, что производная по направлению является линейной комбинацией частных производных, причем направляющие косинусы являются коэффициентами, показывающими вклад в производную по направлению от соответствующей частной производной. В частности,
Из этого следует, что частные производные по х, у, z являются частными случаями производной по направлению осей координат. Касательная плоскость и нормаль к поверхности.
Касательная плоскость и нормаль к поверхности Определение 1. Касательной плоскостью к поверхности Пусть поверхность s задана уравнением F (х, у, z) = 0 и точка P (x 0, y 0, z 0) принадлежит этой поверхности. Выберем на поверхности какую-либо кривую L, проходящую через точку Р. Пусть х = х (t), у = у (t), z = z (t) – параметрические уравнения линии L. Предположим, что: 1) функция F (х, у, z) дифференцируема в точке Р и не все её частные производные в этой точке равны нулю; 2) функции х (t), у (t), z (t) также дифференцируемы. Поскольку кривая принадлежит поверхности s, то координаты любой точки этой кривой, будучи подставленными в уравнение поверхности, обратят его в тождество. Таким образом, справедливо тождественное равенство: F [ x (t), у (t), z (t)] = 0. Продифференцировав это тождество по переменной t, используя цепное правило, получим новое тождественное равенство, справедливое во всех точках кривой, в том числе и в точке P (x 0, y 0, z 0):
Пусть точке Р соответствует значение параметра t 0, то есть x 0 = x (t 0), y 0 = y (t 0), z 0 = z (t 0). Тогда последнее соотношение, вычисленное в точке Р, примет вид
Формула (17) представляет собой скалярное произведение двух векторов. Первый из них – постоянный вектор
не зависящий от выбора кривой на поверхности Второй вектор
расположены в одной плоскости, которая, по определению, является касательной к поверхности s, а точка Р в этом случае называется точкой касания. Вектор Определение 2. Нормалью к поверхности s в точке Р называется прямая, проходящая через точку Р и перпендикулярная к касательной плоскости, построенной в этой точке. Мы доказали существование касательной плоскости, а, следовательно, и нормали к поверхности. Запишем их уравнения:
(18) – уравнение касательной плоскости, построенной в точке P (x 0, y 0, z 0) к поверхности s, заданной уравнением F (х, у, z) = 0; Необходимое условие экстремума функций двух переменных.
Функция z = f (x, y) может иметь экстремум лишь в тех точках, в которых обе частные производные
|
|||||
|
Последнее изменение этой страницы: 2016-08-06; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.01 с.) |

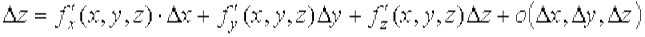 .
. – бесконечно малые функции при Δ l → 0. Разделив обе части равенства на Δ l и учитывая, что
– бесконечно малые функции при Δ l → 0. Разделив обе части равенства на Δ l и учитывая, что ,
, .
. .
. при
при  ,
,  при
при 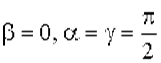 .
.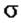 в данной точке P (x 0, y 0, z 0) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.
в данной точке P (x 0, y 0, z 0) называется плоскость, проходящая через точку Р и содержащая в себе все касательные, построенные в точке Р ко всевозможным кривым на этой поверхности, проходящим через точку Р.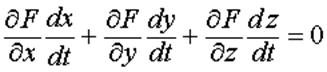 .
. . (17)
. (17) ,
, – касательный в точке Р к линии L, а значит, зависящий от выбора линии на поверхности, то есть является переменным вектором.
– касательный в точке Р к линии L, а значит, зависящий от выбора линии на поверхности, то есть является переменным вектором. При введённых обозначениях равенство (17) перепишем как
При введённых обозначениях равенство (17) перепишем как  . Его смысл таков: скалярное произведение равно нулю, следовательно, векторы
. Его смысл таков: скалярное произведение равно нулю, следовательно, векторы  и
и  перпендикулярны. Выбирая всевозможные кривые (см. рис. 54), проходящие через точку Р на поверхности s, мы будем иметь различные касательные векторы, построенные в точке Р к этим линиям; вектор же
перпендикулярны. Выбирая всевозможные кривые (см. рис. 54), проходящие через точку Р на поверхности s, мы будем иметь различные касательные векторы, построенные в точке Р к этим линиям; вектор же  ; (18)
; (18) обращаются в ноль или перестают существовать.
обращаются в ноль или перестают существовать. ; (19)
; (19)


