
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия разложения функции в ряд ТейлораСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Определение 10.11.1.Пусть функция f (x) в некоторой окрестности точки а имеет производные всех порядков. Степенной ряд по степеням (х - а)
называется рядом Тейлора функции f (x) в точке а. Если а = 0, то ряд
Эти ряды широко используются для получения приближения f (x) в окрестности точки х = а. Заметим, что ряд, составленный для функции f (x), может расходиться или сходиться не к функции f (x). Например, функция Представляет интерес тот случай, когда ряд Тейлора функции f (x) сходится к f (x) в некоторой окрестности точки а. Из ряда Тейлора следует, что его n -й частичной суммой является многочлен Тейлора
Отсюда, если ряд Тейлора сходится к функции f (x), справедливо равенство
где
где х принадлежит некоторой окрестности точки а. Разложим функцию по формуле Тейлора:
где остаточный член представим одним из следующих видов:
Из формулы и равенств и вытекает, что остаток ряда Тейлора Итак, если ряд Тейлора функции f (x), для которой он составлен, сходится в окрестности точки х = 0 к этой функции, то имеет место равенство
Если для какой-нибудь функции формально написан ряд Тейлора, то чтобы доказать, что написанный ряд представляет именно данную функцию, нужно либо доказать, что остаточный член стремится к нулю, либо каким-либо иным способом убедиться, что написанный ряд сходится к данной функции.
10.12. Разложение по степеням х функций
Рассмотрим примеры разложения некоторых функций в ряд Маклорена. 1. Так как
где Покажем, что Так как ряд Функция
Если Тогда Следовательно, для всех значений х полученный ряд Маклорена сходится и представляет функцию
2.
Тогда
где
3. Аналогично, как в предыдущем примере, получаем
где Очевидно,
4. Биномиальный ряд и его частные случаи. Разложим в ряд Маклорена функцию Здесь оценка остаточного члена представляет некоторые трудности, и потому к оценке условий разложимости подойдем несколько иначе. Сначала формально найдем коэффициенты разложения
………………………………………………,
Поэтому
Этот ряд называется биномиальным, найдем его интервал сходимости.
Значит, ряд сходится абсолютно при В самом деле, нетрудно проверить, что функция f (x), определяемая биномиальным рядом, является решением задачи Коши для дифференциального уравнения Заметим, что если m – целое положительное число, то биномиальный ряд превращается в бином Ньютона. Рассмотрим частные случаи биномиального ряда: 1) при m = -1 получаем
2) при m =
3) при m = -
Применим разложение биномиального ряда к разложению других функций. Разложим в ряд Маклорена функцию Подставляя в последнее равенство вместо х выражение На основании теоремы об интегрировании степенных рядов получаем:
Этот ряд сходится для
Приложение рядов к приближенным вычислениям
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 1707; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.32.186 (0.011 с.) |



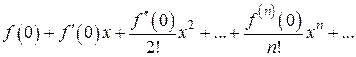 называется рядом Маклорена.
называется рядом Маклорена.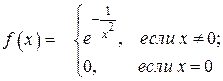 в точке а= 0 имеет производные всех порядков, равные нулю. Поэтому ее ряд Маклорена имеет вид 0+0 х +0 х 2+…, который сходится, но не к нашей функции f (x), не равной нулю ни в какой точке х ¹ 0.
в точке а= 0 имеет производные всех порядков, равные нулю. Поэтому ее ряд Маклорена имеет вид 0+0 х +0 х 2+…, который сходится, но не к нашей функции f (x), не равной нулю ни в какой точке х ¹ 0.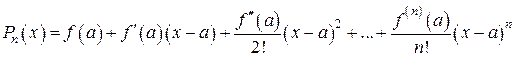 .
.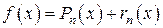 ,
,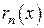 – остаток ряда. Для сходимости ряда Тейлора к функции f (x) необходимо и достаточно выполнения условия
– остаток ряда. Для сходимости ряда Тейлора к функции f (x) необходимо и достаточно выполнения условия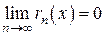 ,
,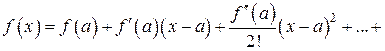
 ,
,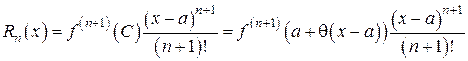 – форма Лагранжа (С находится между а и х, 0 < q <1);
– форма Лагранжа (С находится между а и х, 0 < q <1);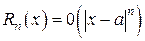 – форма Пеано.
– форма Пеано. , т.е.
, т.е. 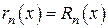 , при выполнении условия.
, при выполнении условия.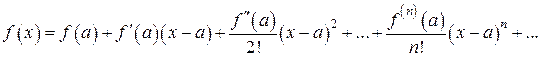
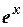 , sin x, cos x,
, sin x, cos x, 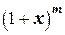
 , а = 0.
, а = 0.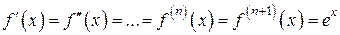 , а
, а 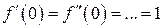 , то
, то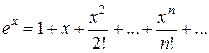 ,
,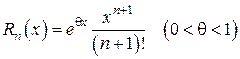 .
.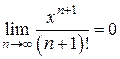 для любого х. Для этого рассмотрим степенной ряд
для любого х. Для этого рассмотрим степенной ряд 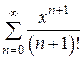 и покажем, что он абсолютно сходится для всех
и покажем, что он абсолютно сходится для всех 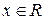 . Действительно,
. Действительно, 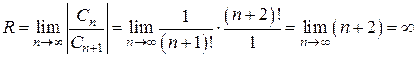 .
. для всех х £ 0 удовлетворяет неравенству
для всех х £ 0 удовлетворяет неравенству .
.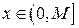 , то
, то 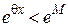 , так как 0 < q < 1.
, так как 0 < q < 1.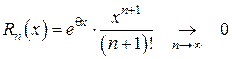 , как произведение функции ограниченной на бесконечно малую.
, как произведение функции ограниченной на бесконечно малую.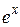 .
.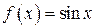 , а = 0.
, а = 0.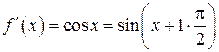 ,
, 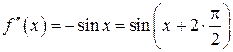 ,
,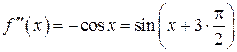 ,
,  , …,
, …,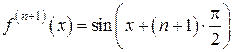 .
. ,
, 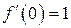 ,
, 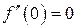 ,
, 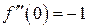 ,
, 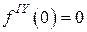 , … и мы имеем разложение
, … и мы имеем разложение  ,
,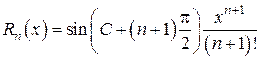 (С находится между 0 и х).
(С находится между 0 и х). , так как
, так как  , а
, а 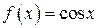 , а = 0.
, а = 0. ,
,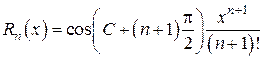 (С находится между 0 и х).
(С находится между 0 и х). , где m - произвольное постоянное число.
, где m - произвольное постоянное число.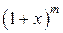 в ряд Маклорена.
в ряд Маклорена. 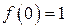 ;
;  Þ
Þ 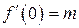 ;
;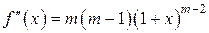 Þ
Þ 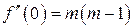 ;
;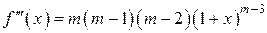 Þ
Þ 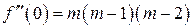 Þ,
Þ,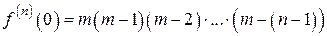 .
.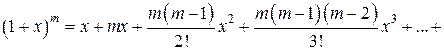
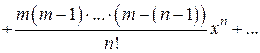
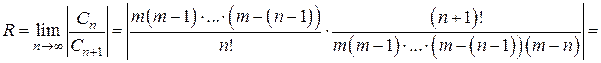
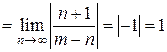 .
. . Покажем, что суммой этого ряда является
. Покажем, что суммой этого ряда является 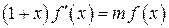 , f (0)=1. Но решением этой же задачи является функция
, f (0)=1. Но решением этой же задачи является функция 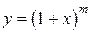 , так как
, так как 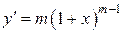 и
и 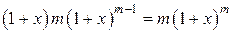 Þ
Þ 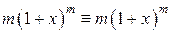 . Отсюда в силу единственности решения задачи Коши получаем
. Отсюда в силу единственности решения задачи Коши получаем 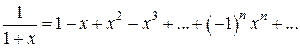 ;
;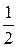 имеем
имеем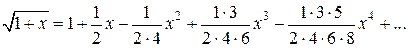 ;
;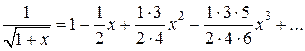
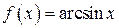 .
. , получим
, получим 

 .
.


