
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды с положительными членами. Теоремы сравненияСодержание книги Поиск на нашем сайте
Пусть задан ряд Так как частичные суммы ряда с положительными членами образуют неубывающую последовательность (S 1< S 2< S 3<…), то этот ряд сходится тогда и только тогда, когда последовательность
Теорема 10.4.1 (признак сравнения 1). Пусть для рядов
(для всех n или начиная с некоторого N). Тогда: 1) если сходится ряд 2) если расходится ряд Признак утверждает, что при выполнении условия из сходимости ряда с большими членами вытекает сходимость с меньшими членами, а из расходимости ряда с меньшими членами вытекает расходимость ряда с большими членами. Доказательство. 1) Пусть ряд
где 2) Пусть ряд При выполнении условий будем говорить, что ряд
Пример 10.4.1. Ряд
Пример 10.4.2. Ряд Замечание 10.4.1.Признак сравнения 1 справедлив только для рядов с положительными членами. Он остается в силе, если некоторые члены 1-го или 2-го ряда – нули. Однако этот признак перестает быть верным, если среди членов ряда есть отрицательные числа. Замечание 10.4.2.Теорема 10.4.1 справедлива и в том случае, если неравенство начинает выполняться лишь для
Теорема 10.4.2 (предельный признак сравнения 2). Пусть члены рядов
Тогда оба ряда сходятся или расходятся одновременно.
Пример 10.4.3. Исследовать на сходимость ряд Решение. Так как
Пример 10.4.4. Исследовать на сходимость ряд Решение. Так как
Признаки Даламбера и Коши Рассмотрим еще три достаточных признака для исследования числовых рядов с положительными членами.
Теорема 10.5.1 (признак Даламбера). Если в ряде
отношение (n +1)-го члена к n -му при n ®¥ имеет конечный предел
то 1) ряд сходится, если р < 1; 2) ряд расходится, если р > 1. (В случае р = 1 ответа на вопрос о сходимости или расходимости ряда теорема не дает, нужны дополнительные исследования.) Доказательство. 1) Пусть р < 1. Рассмотрим число q, удовлетворяющее соотношению р < q < 1. Из определения предела следует, что
Рассмотрим теперь три ряда
Ряд есть сумма геометрической прогрессии с q < 1, следовательно, он сходится. Члены ряда меньше соответствующих членов ряда ввиду выполнения неравенств, поэтому он сходится. Но ряд получается добавлением к сходящемуся ряду конечного числа членов (N -1), поэтому он тоже сходится. 2) Пусть р > 1. Тогда из равенства Замечание 10.5.1.Ряд будет расходиться и в том случае, когда р = ¥. Это следует из того, что если
Пример 10.5.1. Исследовать сходимость ряда
Решение. Здесь
Пример 10.5.2. Исследовать сходимость ряда Решение. Замечание 10.5.2.Если р = 1, но отношение
Пример 10.5.3. Исследовать сходимость ряда
Решение.
В данном случае ряд расходится, так как
Теорема 10.5.2(радикальный признак Коши). Если для ряда с положительными членами существует конечный предел 1) если р < 1, ряд сходится; 2) если р > 1, ряд расходится. Как и в признаке Даламбера, случай р = 1 требует дополнительного исследования. Доказательство практически ничем не отличается от доказательства теоремы 10.5.1, поэтому его приводить не будем.
Пример 10.5.4. Исследовать сходимость ряда
Решение. Применим радикальный признак Коши:
Теорема 10.5.3(интегральный признак Коши). Пусть члены ряда
Пример 10.5.5. Исследовать на сходимость ряд Решение. Положим
т.е. расходится, то в соответствии с интегральным признаком Коши расходится и заданный ряд.
Пример 10.5.6. Исследовать на сходимость обобщенный гармонический ряд
Рассмотрим три случая: 1) пусть р > 1 Þ р -1 > 0, тогда
интеграл конечен и, следовательно, ряд сходится. 2) пусть р < 1 Þ 1- р > 0 и
интеграл расходится и, следовательно, ряд расходится. 3) если р = 1, рассматриваем
Таким образом, ряд Дирихле Заметим, что ни признак Даламбера, ни радикальный признак Коши не решают вопрос о сходимости этого ряда, так как соответствующие пределы равны 1. Обобщенный гармонический ряд (ряд Дирихле), а также ряд, составленный из членов геометрической прогрессии, часто используются как «эталонные» ряды при применении обоих признаков сравнения.
|
||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 430; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.192.250 (0.006 с.) |

 с положительными членами
с положительными членами  . Исследуем вопрос о его сходимости или расходимости.
. Исследуем вопрос о его сходимости или расходимости. его частичных сумм ограничена.
его частичных сумм ограничена. имеет место неравенство
имеет место неравенство
 ,
, – частичная сумма ряда
– частичная сумма ряда  – частичная сумма ряда
– частичная сумма ряда  имеет предел, т.е. ряд
имеет предел, т.е. ряд  должен сходиться и ряд
должен сходиться и ряд  сходится, так как его члены не больше соответствующих членов ряда
сходится, так как его члены не больше соответствующих членов ряда 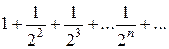
 . Последний ряд сходится, так как его члены, начиная со второго, образуют геометрическую прогрессию со знаменателем
. Последний ряд сходится, так как его члены, начиная со второго, образуют геометрическую прогрессию со знаменателем  . Сумма этого ряда
. Сумма этого ряда  . Следовательно, в силу теоремы 10.4.1 данный ряд тоже сходится, причем его сумма s < 1,5.
. Следовательно, в силу теоремы 10.4.1 данный ряд тоже сходится, причем его сумма s < 1,5. расходится, так как его члены, начиная со второго, больше соответствующих членов гармонического ряда
расходится, так как его члены, начиная со второго, больше соответствующих членов гармонического ряда  , который расходится.
, который расходится. , а не для всех n = 1, 2, 3, …
, а не для всех n = 1, 2, 3, … ,
,  .
. .
. при n ®¥, то сравним этот ряд с обобщенным гармоническим рядом
при n ®¥, то сравним этот ряд с обобщенным гармоническим рядом  (р =2>1), который сходится. Поскольку
(р =2>1), который сходится. Поскольку 
 , то по признаку сравнения 2 исходный ряд сходится.
, то по признаку сравнения 2 исходный ряд сходится. .
.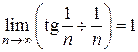 , а ряд
, а ряд  расходится, то расходится и данный ряд по признаку сравнения 2.
расходится, то расходится и данный ряд по признаку сравнения 2.
 ,
, , что для всех
, что для всех  будет иметь место
будет иметь место  Þ
Þ  Þ
Þ  . Запишем это неравенство для различных значений n, начиная с номера N.
. Запишем это неравенство для различных значений n, начиная с номера N.
 (исходный ряд)
(исходный ряд)

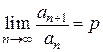 (где р > 1) следует, что, начиная с некоторого номера N, т.е. для
(где р > 1) следует, что, начиная с некоторого номера N, т.е. для  . Þ
. Þ  для всех
для всех  , то, начиная с некоторого номера n = N, будет иметь место неравенство
, то, начиная с некоторого номера n = N, будет иметь место неравенство 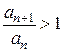 , или
, или 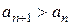 Þ
Þ  .
.
 ,
,  . Следовательно,
. Следовательно,
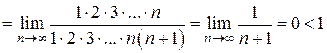 . Ряд сходится.
. Ряд сходится. .
. . Ряд расходится.
. Ряд расходится. для всех номеров n, начиная с некоторого, больше единицы, то ряд расходится. Это следует из того, что если
для всех номеров n, начиная с некоторого, больше единицы, то ряд расходится. Это следует из того, что если 
 .
. .
. , то
, то
 . Ряд сходится.
. Ряд сходится. , где f (x) – неотрицательная монотонно убывающая функция на промежутке
, где f (x) – неотрицательная монотонно убывающая функция на промежутке  , а ³ 1.. Тогда ряд
, а ³ 1.. Тогда ряд  .
. .
. . Функция f (x) непрерывна и монотонно убывает на
. Функция f (x) непрерывна и монотонно убывает на  . Так как несобственный интеграл
. Так как несобственный интеграл ,
,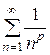 . Эта функция удовлетворяет всем условиям теоремы 10.5.3. Рассмотрим несобственный интеграл
. Эта функция удовлетворяет всем условиям теоремы 10.5.3. Рассмотрим несобственный интеграл .
. , т.е
, т.е , т.е.
, т.е. , ряд расходится.
, ряд расходится.


