
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютно и условно сходящиеся рядыСодержание книги Поиск на нашем сайте
Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные числа. Рассмотренные в п.10.6 знакочередующиеся ряды являются, очевидно, частным случаем знакопеременных рядов. Дадим один важный достаточный признак сходимости знакопеременного ряда.
Теорема 10.7.1.Если знакопеременный ряд
таков, что ряд, составленный из абсолютных величин его членов,
сходится, то и данный знакопеременный ряд также сходится. Доказательство. Пусть Пусть, далее,
По условию
т.е. знакопеременный ряд сходится. Доказанная теорема дает возможность судить о сходимости некоторых знакопеременных рядов. Исследование вопроса о сходимости сводится в этом случае к исследованию рядов с положительными членами.
Пример 10.7.1. Исследовать сходимость ряда
где a - любой угол (в зависимости от a Решение. Рассмотрим два ряда:
и
Ряд сходится, как ряд Дирихле (р = 3 > 1). Члены ряда не больше соответственных членов ряда (так как Заметим, что этот признак сходимости является только достаточным признаком сходимости, но не необходимым: существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся.
Пример 10.7.2. Ряд В связи с этим полезно ввести понятие об абсолютной и условной сходимости знакопеременных рядов и на основе этих понятий классифицировать знакопеременные ряды.
Определение 10.7.1.Знакопеременный ряд
называется абсолютно сходящимся, если сходится ряд
Если же знакопеременный ряд сходится, а ряд расходится, то данный ряд называется условно, или неабсолютно, сходящимся рядом. Таким образом, ряд
Пример 10.7.3. Знакопеременный ряд
есть ряд абсолютно сходящийся, так как ряд из абсолютных величин его
как было показано в п.10.5 при помощи признака Даламбера, сходится.
|
|||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 398; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.71.243 (0.007 с.) |



 и
и  – суммы n первых членов рядов и.
– суммы n первых членов рядов и. – сумма всех положительных, а
– сумма всех положительных, а  – сумма абсолютных величин всех отрицательных членов среди первых n членов ряда; тогда
– сумма абсолютных величин всех отрицательных членов среди первых n членов ряда; тогда ,
,  .
.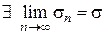 ;
;  и
и  . Из соотношения
. Из соотношения  ,
,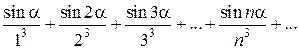
 может иметь любой знак).
может иметь любой знак).

 ); следовательно, ряд тоже сходится по первому признаку сравнения. Но тогда в силу доказанной теоремы данный знакопеременный ряд тоже сходится.
); следовательно, ряд тоже сходится по первому признаку сравнения. Но тогда в силу доказанной теоремы данный знакопеременный ряд тоже сходится. сходится по теореме Лейбница, хотя ряд из абсолютных величин его членов
сходится по теореме Лейбница, хотя ряд из абсолютных величин его членов 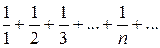 является гармоническим и, как известно, расходится.
является гармоническим и, как известно, расходится.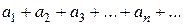

 , рассмотренный в примере 10.7.2, условно сходящийся, а ряд абсолютно сходящийся.
, рассмотренный в примере 10.7.2, условно сходящийся, а ряд абсолютно сходящийся.
 ,
,


