
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Разложение в ряд Фурье четных и нечетных функцийСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть f (x) - четная 2p-периодическая функция. Тогда
т.е. ряд Фурье для четной функции имеет вид
Аналогично, если f (x) - нечетная 2p-периодическая функция, то а 0 = 0, аn = 0, а ряд Фурье для нечетной функции имеет вид
Таким образом, четная 2p-периодическая функция разлагается в ряд Фурье только по косинусам, а нечетная 2p-периодическая функция раскладывается в ряд Фурье только по синусам.
Пример 10.15.1. Разложить в ряд Фурье 2p-периодическую функцию Решение. Функция
Так как функция кусочно-монотонна, ограничена и непрерывна, то это равенство выполняется во всех точках. Полагая х = p в этом равенстве, получим
Полагая х = 0, получаем:
10.16. Разложение в ряд Фурье функций, заданных на
Пусть f (x) есть периодическая функция с периодом Сделаем замену переменной по формуле
Тогда функция
Ее можно разложить в ряд Фурье на [-p, p]:
где
Вернемся теперь к старой переменной х:
Тогда будем иметь
а формула примет вид
Если f (x) - четная функция, то bn = 0, если же f (x) - нечетная функция, то а 0 = 0, аn = 0,
Пример 10.16.1. Разложить в ряд Фурье периодическую функцию f (x) с периодом
Решение. Все условия теоремы Дирихле выполняются. Так как функция четная, то bn = 0,
Следовательно,
Пусть х = 0,
О разложении в ряд Фурье непериодических функций Пусть функция f (x) задана на [0, p]. Чтобы разложить f (x) на этом отрезке в ряд Фурье, доопределим ее на отрезке [-p, 0]. В результате получим функцию, заданную на всем отрезке [-p, p], которую уже можно разложить в ряд Фурье. Ясно, что получившийся ряд будет зависеть от характера продолжения первоначальной функции на [-p, 0]. Рассмотрим два возможных случая. 1. Если продолжить (доопределить) f (x) четным образом с отрезка [0, p] на отрезок [-p, 0] (рис.10.17.1), то получим четную функцию, которая, как известно, раскладывается в ряд Фурье только по косинусам. 2.
Вопросы к экзамену по модулю №10
1. Числовые ряды. Сходимость и сумма ряда. 2. Простейшие действия над рядами. Необходимый признак сходимости. Гармонический ряд. 3. Ряды с положительными членами. Теоремы сравнения. 4. Признаки сходимости Даламбера и Коши. 5. Знакочередующиеся ряды. Теорема Лейбница. 6. Знакопеременные ряды. Абсолютная и условная сходимость. 7. Функциональные ряды. Область сходимости. 8. Степенные ряды. Теорема Абеля. 9. Интервал и радиус сходимости степенных рядов. 10. Интегрирование и дифференцирование степенных рядов. 11. Ряды Тейлора и Маклорена. Достаточные условия разложения функций. 12. Разложение в ряд Маклорена 13. Приложения рядов к приближенному вычислению значений функций и определенных интегралов. 14. Приложения рядов к решению дифференциальных уравнений. 15. Ряд Фурье. Коэффициенты Фурье. Теорема Дирихле. 16. Разложение в ряд Фурье четных и нечетных функций, заданных на (-p, p). 17. Разложение в ряд Фурье 18. О разложении в ряд Фурье непериодических функций.
|
|||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 678; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.104.103 (0.006 с.) |

 является нечетной, а
является нечетной, а  - четной функцией. Следовательно,
- четной функцией. Следовательно,  ,
,  . Согласно формулам - для коэффициентов ряда Фурье получаем
. Согласно формулам - для коэффициентов ряда Фурье получаем ,
,  , bn = 0,
, bn = 0, .
. - нечетная, а
- нечетная, а  - четная функция. В этом случае имеем:
- четная функция. В этом случае имеем: ,
, .
. , заданную на [-p, p].
, заданную на [-p, p]. .
.


 . Значит, ряд Фурье данной функции имеет вид
. Значит, ряд Фурье данной функции имеет вид .
. Þ
Þ  Þ
Þ . Мы нашли сумму обобщенного гармонического ряда для р = 2,
. Мы нашли сумму обобщенного гармонического ряда для р = 2,  .
.

 , вообще говоря, отличным от 2p. Разложим ее в ряд Фурье.
, вообще говоря, отличным от 2p. Разложим ее в ряд Фурье. .
. будет периодической функцией от t с периодом 2p. Действительно,
будет периодической функцией от t с периодом 2p. Действительно, .
. ,
, ,
,  ,
,  .
.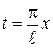 ,
,  .
. ,
,  ,
,  ,
, .
. ,
,  ;
; .
. задается равенством
задается равенством  .
.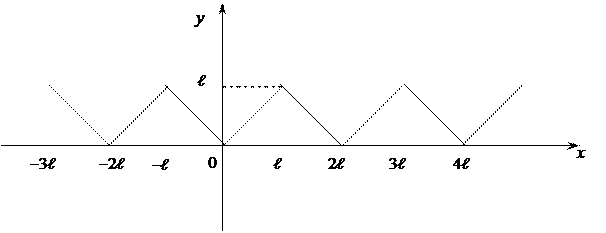
 ,
,
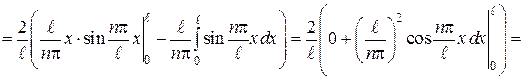
 .
.
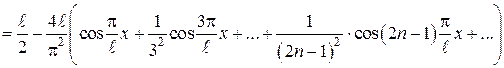 .
. Þ
Þ  .
. Аналогично, продолжая f (x) нечетным образом с отрезка [0, p] на отрезок [-p, 0] (рис.10.17.2), то получим нечетную функцию, разлагающуюся в ряд Фурье только по синусам.
Аналогично, продолжая f (x) нечетным образом с отрезка [0, p] на отрезок [-p, 0] (рис.10.17.2), то получим нечетную функцию, разлагающуюся в ряд Фурье только по синусам.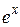 , sin x, cos x,
, sin x, cos x, 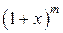 .
.


