
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряд Фурье в тригонометрической формеСодержание книги
Поиск на нашем сайте
Ряд Фурье в тригонометрической форме
Выражение (1) называется тригонометрическим рядом Фурье, его коэффициенты определяются следующим образом:
Если исследуемый сигнал является четной функцией времени, т.е. S(t) = S(–t), то в (1) синусоидальные составляющие обращаются в нуль (bп = 0). Если сигнал является нечетной функцией времени, т.е. S(–t) = –S(t), то в (1) косинусоидальные составляющие обращаются в нуль (ап = 0). В общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую а0 /2, равную среднему значению сигнала на заданном интервале времени, и бесконечный набор гармоник с частотами, кратными основной частоте периодической последовательности ωn = nω1. Каждая гармоника ряда (1) характеризуется собственными амплитудой и фазой, которые являются основными частотными характеристиками любого периодического сигнала. Амплитудная характеристика периодического сигнала определяется из следующих соображений:
Фазовая характеристика определяется:
Используя (5) и (6), тригонометрический ряд Фурье можно записать в виде:
Графическое построение, отображающее коэффициенты ряда Фурье для конкретного сигнала, называется спектральнойдиаграммой. Различают амплитудные и фазовые диаграммы.
Амплитудные Фазовые
A2 A1 Φ1 A0 Φ0 A3 Φ2 Φ3
0 ω1 2ω1 3ω1 ωn 0 ω1 2ω1 3ω1 ωn
Для периодических сигналов и амплитудная, и фазовая характеристики всегда являются дискретными или линейчатыми. Ряд Фурье в комплексной форме Используя формулы Эйлера, можно получить другое симметричное и равноправное представление ряда Фурье – его комплексную форму:
Подставляя (9) в (8), получаем ряд Фурье в комплексной форме:
где Между амплитудами гармоник тригонометрического ряда Фурье и коэффициентами его комплексной формы существует элементарная связь:
Энергия периодического сигнала в промежутке времени [t1, t2] на сопротивлении, равном 1 Ом, вычисляется по формуле:
Среднюю мощность любого сигнала можно вычислить по формуле:
Таким образом, средняя за период мощность периодического сигнала:
Используя тригонометрическую форму ряда Фурье и учитывая, что с0 = а0/2 и
Если s(t) представляет собой ток i(t), то при прохождении его через сопротивление r выделяется мощность (средняя)
где I0 – постоянная составляющая тока.
Задание. Для предложенных в соответствии со своим вариантом видов сигналов: 1. Записать ряд Фурье в тригонометрической и комплексной форме. 2. Составить общие выражения для расчета тригонометрических и комплексных амплитуд и фаз гармонических составляющих данных сигналов. 3. Найти значения амплитуд и фаз первых пяти гармоник для конкретных заданных параметров анализируемых сигналов. 4. Построить графики амплитудного и фазового спектров. 5. Определить полную (среднюю за период) мощность данных сигналов и мощности, приходящиеся на постоянную составляющую и каждую из первых пяти гармоник. 6. Найти эффективную ширину спектра, в которой сосредоточено 90% полной мощности данных сигналов.
Исходные данные для расчетов. 1. Меандр: а) четный, б) нечетный. 2. Пилообразное колебание. 3. Гармоническое колебание: a) s(t) = Е /cos(pt/T)/; б) s(t) = Е /sin (pt/T)/. 4. Последовательность: а) четная; б) нечетная – прямоугольных униполярных импульсов.
Контрольные вопросы: 1. Каков физический смысл постоянной составляющей периодического сигнала? 2. Существует ли различие между спектральными диаграммами периодического сигнала при использовании амплитуд гармоник тригонометрического ряда Фурье и коэффициентов комплексного ряда? Если да, то в чем оно проявляется? 3. Каковы размерности амплитудного и фазового спектров периодических сигналов? 4. Каков физический смысл квадрата нормы функции сигнала? 5. Отличаются ли между собой амплитудные и фазовые диаграммы для четных и нечетных функций одинакового вида? Если да, то как? 6. Изменятся ли амплитудные и фазовые спектры при увеличении длительности импульсов, составляющих данную периодическую последовательность? Если да, то почему и как? 7. Почему спектральные диаграммы периодических сигналов всегда дискретны? 8. Зависит ли значение средней за период энергии сигнала от его положения на оси времени, четности или нечетности описывающей его функции? 9. Определите и поясните зависимость между изменением длительности импульсов, составляющих периодическую последовательность, и количеством гармоник, приходящихся на эффективную ширину спектра сигнала. Исходные данные для расчетов. 1. Прямоугольный: а) четный; б) нечетный импульсы. 2. Треугольный импульс. 3. Косинусоидальный и синусоидальный импульсы: a) s(t) = E cos wot; б) s(t) = E sin wot. 4. Экспоненциальный импульс: s(t) = U exp (-at).
Контрольные вопросы: 1. Как можно определить физический смысл спектральной плотности? 2. Какими характерными особенностями отличаются спектральные плотности для сигналов, являющихся четными функциями времени? 3. Какими функциями частоты являются действительная и мнимая части спектральной плотности? 4. В чем принципиальное отличие амплитудных и фазовых спектров периодических и непериодических сигналов? 5. Определите значение спектральной плотности сигнала при изменении его масштаба времени с коэффициентом к = – 1 и проанализируйте полученный результат. 6. Какому виду импульсов соответствует свойство смещения спектра сигнала, используемое при умножении его функции на гармоническое колебание? 7. В чем характерная особенность спектра дельта-функции? 8. Какую роль играет фаза спектральной плотности сигнала при определении его энергетического спектра? 9. Могут ли два нетождественных сигнала обладать одним и тем же энергетическим спектром?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 3 «ДЕЛИТЕЛИ НАПРЯЖЕНИЯ И ТОКА» Цель: изучить правила делителей напряжения и тока и проанализировать предложенные схемы. Делитель напряжения На рис. 1 представлена простейшая схема делителя напряжения на двух резисторах R1 и R2. К цепи приложено напряжение источника постоянного тока Е. Через резисторы протекает ток I (последовательное включение), на резисторе R1 падает напряжение U1, на резисторе R2 – напряжение U2:
Задание. По формулам (1) рассчитать падение напряжения на резисторах R1 и R2 для данных, приведенных в табл.1. Результаты расчетов занести в таблицу. Порядок выполнения. Собрать схему делителя, представленную на рис. 1.

Рис. 1 – Схема делителя напряжения
Провести экспериментальную проверку полученных результатов. Изменяя в схеме значения сопротивлений и напряжения источника питания, заполните таблицу 1. Табл.1
По результатам измерений построить зависимости U1=f(R1) при R2=const и U2= f(R2) при R1=const для двух значений V3. Сравнить и проанализировать полученные теоретические и экспериментальные результаты.
Делитель тока На рис. 2 представлена простейшая схема из двух параллельно включенных сопротивлений R1 и R2. К ним приложено напряжение источника постоянного тока Е. Через резистор R1 протекает ток I1, через резистор R2 ток I2. Через оба резистора протекает суммарный ток
В свою очередь
Рис. 2 – Схема делителя тока
Задание. По формулам (2) рассчитать токи через резисторы R1 и R2 для данных, приведенных в табл. 2. Результаты расчетов занести в таблицу. Порядок выполнения. Собрать схему делителя, представленную на рис. 3.
Рис. 3 – Схема параллельной цепи
Провести экспериментальную проверку полученных результатов. Изменяя в схеме значения сопротивлений и напряжения источника питания, заполнить таблицу 2. Табл.2.
По результатам измерения построить зависимости I=f(Ro) для двух значений V3. Сравнить и проанализировать полученные теоретические и экспериментальные результаты.
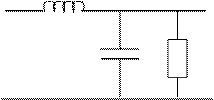
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 4 «ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ RC-ЦЕПЕЙ» Цель: изучить частотные характеристики RC-цепей, сравнить и проанализировать их для двух предложенных схем. Порядок выполнения. Как отмечалось выше, в параллельном колебательном контуре наблюдается резонанс токов, поэтому на контур подается сигнал с источника тока J1(коэффициент передачи по напряжению равен 1). Для измерения токов можно воспользоваться источниками напряжения, управляемыми током (IU1 и IU2 на рис. 29). Напряжение на выходе этих элементов пропорционально токам, протекающих в первичной цепи этих источников. Коэффициент передачи этих источников равен отношению выходного напряжения к току в первичной цепи и имеет размерность Ом. В данном примере этот коэффициент равен 1В/1А=1 Ом. Таким образом, сигналы, подаваемые на вход измерительных приборов (осциллографа и плоттера), будут пропорциональны токам, протекающим во входной цепи и через емкость соответственно. На плоттере удобно наблюдать и измерять АЧХ и ФЧХ. С помощью осциллографа можно наблюдать соотношение между входным и выходным сигналом (сигналы пропорциональны токам!). Для этих исследований необходимо изменять частоту источника тока J1.
Рис. 29 – Схема измерения параметров параллельного колебательного контура
Способы измерения с помощью опций меню Analysis и измерителя АЧХ и ФЧХ подробно изложены в работе 6. Используя описанные методики, измерить и занести в таблицу 13 параметры амплитудно-частотной и фазо-частотной характеристик параллельного контура для следующих значений элементов: А). R=0,1 Ом, С=1 мкФ и L=1, 2 …..10 мГн; Б). R=0,1 Ом, L= 1 мГн и С=1, 2……10 мкФ; В).L= 1 мГн, С=1 мкФ и R =1, 2 …….10 Ом. По результатам измерений построить амплитудно-частотные и фазо-частотные характеристики, а также годографы комплексной передаточной функции параллельного резонансного контура. Построить зависимости характеристик контура – резонансной частоты, добротности, полосы частот – от значений R, L и C. Табл.13
Контрольные вопросы: 1. Как определяются токи в цепи синусоидального тока с параллельным соединением резистора, индуктивности и ёмкости. Запишите закон Ома в комплексной форме. 2. Что такое треугольник проводимостей? Как его построить? 3. Какую цепь называют параллельным колебательным контуром? 4. При каком условии в параллельном колебательном контуре наступает резонанс? Почему резонанс в такой цепи называют резонансом токов? 5. Как определяется резонансная частота? 6. Что называют характеристическим сопротивлением контура и добротностью контура? 7. Изменением каких величин в параллельном колебательном контуре можно достичь резонанса токов?
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 8 «ИССЛЕДОВАНИЕ СВЯЗАННЫХ КОНТУРОВ» Цель: изучить основные виды связи и их влияние на свойства, временные и частотные характеристики связанных контуров. Реализация НЧ-фильтров Для реализации принципиальной схемы фильтра используется так называемый структурный синтез, когда цепь образуется каскадным включением звеньев, и общий частотный коэффициент передачи такого устройства определяется по формуле: K(p)=K1(p) K2(p)... Kn(p). Коэффициенты передачи звеньев должны реализовывать те полюса передаточной функции, которые были получены на этапе аппроксимации. Для синтеза НЧ-фильтров требуются каскады двух видов: звенья первого порядка, которые имеют один вещественный полюс, и звенья второго порядка, которые имеют пару комплексно-сопряженных полюсов. В качестве звена первого порядка можно использовать интегрирующую RC-цепь, частотный коэффициент передачи которой и единственный полюс определяются следующим образом:
Сопоставляя значения найденного на этапе аппроксимации нормированного полюса и конкретного для данного звена, можно определить номиналы входящих в схему элементов (один из них выбирается произвольно): Р1=Рнωс; В качестве звена второго порядка можно использовать любой Г-образный четырехполюсник, содержащий R, L, C элементы, дифференциальное уравнение которого имеет соответственно пару комплексно-сопряженных корней: L
C R Uвх Uвых
Uвх=UL+UR;
Тогда переход от нормированных полюсов к обычным частотам осуществится по формуле: P1,2= Pн1,2ωс. Реализация ВЧ-фильтров Для того, чтобы на основе синтезированного ФНЧ реализовать ФВЧ с той же частотой среза, необходимо осуществить замену переменной:
В результате такой замены конденсаторы и катушки индуктивности меняются местами с соответствующей заменой номиналов.
Резистивные элементы при этом остаются без изменения. Реализация полосовых фильтров осуществляется в результате следующей замены частотной переменной, при этом частота среза соответствующего ФНЧ становится центральной частотой полосового фильтра ω0:
В результате такой замены:
Таким образом, ФНЧ является фильтром-прототипом, параметры которого позволяют перейти к соответствующим схемам полосовых фильтров и ФВЧ.
Задание: Для приведенных ниже в соответствии со своим вариантом исходных параметров определить: 1. Функцию частотного коэффициента передачи мощности Кр (wн) и построить ее график. 2. Полюса функции Кр (wн). 3. Передаточную функцию фильтра К(р). 4. Тип структурной схемы фильтра, соответствующей полученной передаточной функции. 5. Номиналы элементов, входящих в схему. 6. Соответствующие схемы ФВЧ и ПФ с той же частотой среза. 7. Промоделировать полученные схемы ФВЧ и ПФ в программе Electronics Workbench и построить их АЧХ. 8. Оформить полученные теоретические расчеты и графические материалы.
Исходные данные для расчетов:
Контрольные вопросы: 1. Сформулируйте технические требования к АЧХ для фильтров верхних частот и полосовых. 2. По какому правилу отбираются полюса для передаточной функции четырехполюсника? 3. Можно ли, зная порядок фильтра, определить количество необходимых для него звеньев? 4. Из каких соображений осуществляются замены элементов при переходе от ФНЧ к ФВЧ и ПФ? Какое условие должно выполняться при таких заменах? 5. Четырехполюсники какого типа можно использовать в качестве звеньев второго порядка при синтезе фильтров? 6. Как соотносятся между собой полюса нормированной частоты, полученные на этапе аппроксимации, со значениями полюсов реального четырехполюсника? 7. Как значение e влияет на вид АЧХ фильтра Чебышева? 8. Как изменяется АЧХ фильтров Баттерворта и Чебышева с ростом порядка фильтра?
Ряд Фурье в тригонометрической форме
Выражение (1) называется тригонометрическим рядом Фурье, его коэффициенты определяются следующим образом:
Если исследуемый сигнал является четной функцией времени, т.е. S(t) = S(–t), то в (1) синусоидальные составляющие обращаются в нуль (bп = 0). Если сигнал является нечетной функцией времени, т.е. S(–t) = –S(t), то в (1) косинусоидальные составляющие обращаются в нуль (ап = 0). В общем случае периодический сигнал содержит не зависящую от времени постоянную составляющую а0 /2, равную среднему значению сигнала на заданном интервале времени, и бесконечный набор гармоник с частотами, кратными основной частоте периодической последовательности ωn = nω1. Каждая гармоника ряда (1) характеризуется собственными амплитудой и фазой, которые являются основными частотными характеристиками любого периодического сигнала. Амплитудная характеристика периодического сигнала определяется из следующих соображений:
Фазовая характеристика определяется:
Используя (5) и (6), тригонометрический ряд Фурье можно записать в виде:
Графическое построение, отображающее коэффициенты ряда Фурье для конкретного сигнала, называется спектральнойдиаграммой. Различают амплитудные и фазовые диаграммы.
Амплитудные Фазовые
A2 A1 Φ1 A0 Φ0 A3 Φ2 Φ3
0 ω1 2ω1 3ω1 ωn 0 ω1 2ω1 3ω1 ωn
Для периодических сигналов и амплитудная, и фазовая характеристики всегда являются дискретными или линейчатыми.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 839; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.140.100 (0.009 с.) |

 (1)
(1) (2)
(2) (3)
(3) (4)
(4)
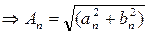 (5)
(5) (6)
(6) (7)
(7) An Φn
An Φn (8)
(8) (9)
(9) (10)
(10)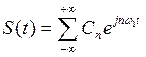 , (11)
, (11) . (12)
. (12) . (13)
. (13) . (14)
. (14) . (15)
. (15) . (16)
. (16) , получаем
, получаем (17)
(17) , (18)
, (18)



 ,
,  ,
, 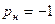 .
.
 ;
;
 .
.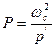
 ;
; 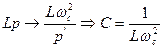 .
. .
. ;
; .
.


