
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряд Фурье для четных и нечетных функций.Содержание книги
Поиск на нашем сайте
Отметим следующие свойства четных и нечетных функций: 1) 2) Произведение двух четных и нечетных функций является четной функцией. 3) Произведение четной и нечетной функций – нечетная функция. Если f(x) – четная периодическая функция с периодом
Таким образом, для четной функции ряд Фурье записывается:
Аналогично получаем разложение в ряд Фурье для нечетной функции:
Пример 2. Построить эскиз графика, разложить в ряд Фурье функцию y=x, Решение. Эта функция непрерывна на отрезке
Подставляя коэффициенты в ряд Фурье, получаем разложение На концах отрезка Построим график S3(x)
Вопросы для самопроверки 1. Запишите ряд Фурье для четной функции 2. Запишите ряд Фурье для нечетной функции Ряды Фурье для функций произвольного периода. Ряд Фурье для функции
Для четной функции произвольного периода разложение в ряд Фурье имеет вид: Для нечетной функции: Пример 3. Разложить в ряд Фурье периодическую функцию Решение. Построим эскиз графика функции
Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. Заданная функция четная, поэтому в разложении ее в ряд Фурье отсутствуют синусы, т. е. В нашем случае l =2, поэтому Таким образом, Окончательно получаем Построим график частичной суммы S3(x)
Вопросы для самопроверки 1. Запишите ряд Фурье для функции с произвольным периодом 2. Запишите ряд Фурье для четной функции с произвольным периодом 3. Запишите ряд Фурье для нечетной функции с произвольным периодом Разложение в ряд Фурье непериодической функции. Задача разложения непериодической функции в ряд Фурье, в принципе не отличается от разложения в ряд Фурье периодической функции. Допустим, что функция f(x) задана на отрезке
f(x)
a - 2T a a b a+2T a + 4T x
Таким образом, функция f(x) была доопределена. Полученная функция Если функция f(x) задана на отрезке, равном 2 l, то ее разложение ничем не отличается от разложения в ряд периодической функции с периодом 2 l. Если же отрезок, на котором задана функция, меньше, чем 2 l, то ее можно продолжить на отрезок [ a; a+ 2 l ], так, чтобы условия разложимости в ряд Фурье сохранялись. Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2 l может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но все они будут совпадать с заданной функцией f(x) на отрезке Пример 4. Разложить в ряд Фурье функцию Решение. Будем считать функцию периодической с периодом
Тогда, ряд Фурье для этой функции будет иметь следующий вид:
Таким образом
Вопросы для самопроверки 1. Запишите ряд Фурье для непериодической функции, заданной на некотором интервале (а,b). §5. Задача о разложении в ряд Фурье функции, заданной на отрезке [0, π] ([0.l]) по синусам или по косинусам Этот случай можно свести к предыдущему. Для решения задачи достаточно дополнить определение этой функции для значений x в промежутке Если доопределить данную функцию так, чтобы при Если доопределить данную функцию так, чтобы при Графически это можно представить следующим образом:
Из сказанного следует: заданную на промежутке Замечание 1. Нетрудно заметить, что как в случае разложения непериодической функции Замечание 2. В случае разложения непериодической функции
Пример 5. Разложить в ряд Фурье функцию Решение. Продолжив заданную функцию
Найдем коэффициенты Фурье для этой функции. Так как она нечетна и, кроме того, симметрична относительно оси абсцисс при совмещении двух полупериодов, ее ряд Фурье содержит только нечетные синусоиды: Окончательно получаем Построим график S3(x)
Во многих задачах приходится разлагать в ряд Фурье функцию, заданную на промежутке Характер сходимости ряда Фурье определяется свойствами заданной функции в граничных точках Если теперь допустить, что Вопросы для самопроверки 1. Запишите ряд Фурье для разложения функции, заданной на промежутке
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2996; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.109.141 (0.008 с.) |


 , удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:
, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать: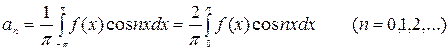
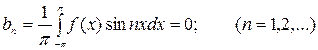
 ,
, 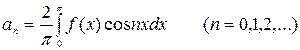


 периодическую с периодом
периодическую с периодом  , то есть на отрезке длиной в период, поэтому допускает разложение в ряд Фурье, сходящейся к ней в каждой точке этого отрезка. Построим график этой функции.
, то есть на отрезке длиной в период, поэтому допускает разложение в ряд Фурье, сходящейся к ней в каждой точке этого отрезка. Построим график этой функции.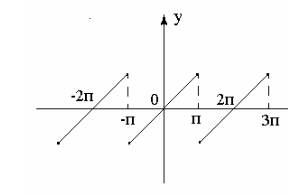
 - нечётная, поэтому
- нечётная, поэтому 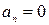 . Ряд Фурье имеет вид:
. Ряд Фурье имеет вид:  . Вычислим коэффициенты
. Вычислим коэффициенты  :
: 
 =
=  .
.
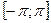
 , поэтому
, поэтому 
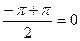 .
.
 периода
периода  , непрерывной или имеющей конечное число точек разрыва первого рода на отрезке
, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке 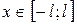 имеет вид:
имеет вид:  , где
, где .
.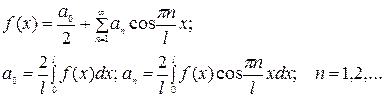 .
. .
. с периодом
с периодом  на отрезке
на отрезке  .
.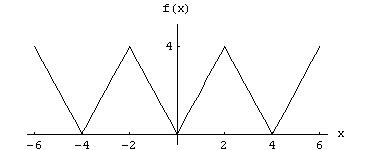
 = 0. Для четной функции произвольного периода 2 l разложение в ряд Фурье имеет вид:
= 0. Для четной функции произвольного периода 2 l разложение в ряд Фурье имеет вид:  .
.
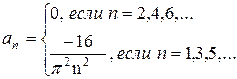


 и является на этом отрезке кусочно - монотонной. Рассмотрим произвольную периодическую кусочно - монотонную функцию
и является на этом отрезке кусочно - монотонной. Рассмотрим произвольную периодическую кусочно - монотонную функцию 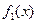 c периодом
c периодом  , совпадающую с функцией f(x) на отрезке
, совпадающую с функцией f(x) на отрезке  , содержащий отрезок
, содержащий отрезок 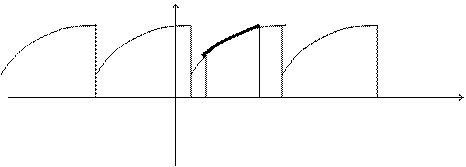 y
y , во всех точках отрезка
, во всех точках отрезка  совпадает с функцией f(x), поэтому можно считать, что функция f(x) разложена в ряд Фурье на отрезке
совпадает с функцией f(x), поэтому можно считать, что функция f(x) разложена в ряд Фурье на отрезке  .
.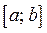 .
.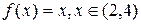 .
.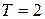 , т.е.
, т.е.  . Построим график этой функции
. Построим график этой функции
 .
.



 . Построим график S3(x).
. Построим график S3(x). 

 по свободному выбору. Теперь уже
по свободному выбору. Теперь уже  будет определена на отрезке
будет определена на отрезке  . Далее поступаем так, как описано в §3. В силу того, что мы свободны в выборе вида функции на промежутке
. Далее поступаем так, как описано в §3. В силу того, что мы свободны в выборе вида функции на промежутке 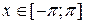
 , то в результате получится четная функция в промежутке
, то в результате получится четная функция в промежутке 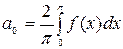 ,
,  . Таким образом, заданную на отрезке
. Таким образом, заданную на отрезке  функцию
функцию 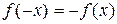 , то в результате получится нечетная функция, рассматриваемая на промежутке
, то в результате получится нечетная функция, рассматриваемая на промежутке  . В этом случае функция
. В этом случае функция 
 периодическое продолжение производится аналогично функции, определенной на
периодическое продолжение производится аналогично функции, определенной на 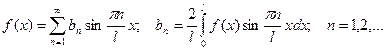 ,
,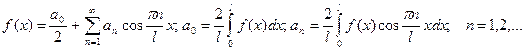 для четной функции.
для четной функции.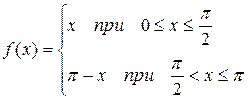 по синусам.
по синусам. .
.
 ,
,  .
. 

 .
.
 и
и  . Если функция
. Если функция  а коэффициенты ряда синусов - со скоростью
а коэффициенты ряда синусов - со скоростью 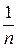 .
.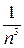 , подходящей для многих приложений рядов Фурье.
, подходящей для многих приложений рядов Фурье. , по синусам и косинусам
, по синусам и косинусам


