
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрический ряд. Ряд Фурье.Содержание книги Поиск на нашем сайте В науке и технике часто приходится иметь дело с периодическими явлениями, т.е. такими, которые воспроизводятся через определённый промежуток времени T, называемый периодом. Простейшей из периодических функций (если не считать постоянной) является синусоидальная величина: Asin (
которые, если не считать постоянной, имеют частоты Для примера мы воспроизводим здесь сложение трех синусоидальных величин:
Этот график значительно отличается от синусоиды. Еще в большей степени это имеет место для суммы бесконечного ряда, составленного из слагаемых этого вида. Поставим вопрос: можно ли данную периодическую функцию периода Т представить в виде суммы конечного или хотя бы бесконечного множества синусоидальных величин? Оказывается, по отношению к большому классу функций на этот вопрос можно дать утвердительный ответ, но это только если привлечь именно всю бесконечную последовательность таких слагаемых. Геометрически это означает, что график периодической функции получается путем наложения ряда синусоид. Если же рассматривать каждую синусоидальную величину как некоторое гармоническое колебательное движение, то можно сказать, что это сложное колебание, характеризуемое функцией Важно отметить, что подобные разложения часто оказываются полезными и при исследовании функций, заданных лишь в определенном конечном промежутке и вовсе не порожденных никакими колебательными явлениями. Определение. Тригонометрическим рядом называется ряд вида:
Действительные числа Если ряд представленного выше типа сходится, то его сумма является периодической функцией с периодом 2p. Определение. Коэффициентами Фурье тригонометрического ряда называются:
Определение. Рядом Фурье для функции f(x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f(x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f(x) разлагается в ряд Фурье. Теорема. (Теорема Дирихле) Если функция При этом ряд Фурье функции f(x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции Функция, удовлетворяющая условиям этой теоремы, называется кусочно – гладкой на отрезке
Рассмотрим примеры на разложение функции в ряд Фурье. Пример 1. Разложить в ряд Фурье функцию f(x)=1-x, имеющую период 2p и заданную на отрезке Решение. Построим график этой функции
Эта функция непрерывна на отрезке Применим формулу интегрирования по частям и найдем
Это равенство имеет место во всех точках, кроме точек
Приведем алгоритм разложения функции Общий порядок решения поставленной задачи сводится к следующему: 1. построение графика заданной функции 2. вычисление коэффициентов 3. составление ряда Фурье заданной функции f(x) в точках ее непрерывности: 4. определение точек разрыва функции f(x); 5. нахождение среднего арифметического предельных значений функции f(x) справа и слева в точке разрыва Замечание. При вычислении коэффициентов Фурье мы можем заменять промежуток интегрирования Вопросы для самопроверки 1. Дайте определение гармонического колебания 2. Дайте определение ряда Фурье 3. Запишите коэффициенты ряда Фурье 4. Сформулируйте теорему Дирихле
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 597; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.006 с.) |

 x +
x +  ), гармоническое колебание, где
), гармоническое колебание, где  . Из таких простейших периодических функций могут быть составлены более сложные. Очевидно, что составляющие синусоидальные величины должны быть разных частот, так как сложение синусоидальных величин одной и той же частоты приводит к синусоидальной величине той же частоты. Если сложить несколько величин вида
. Из таких простейших периодических функций могут быть составлены более сложные. Очевидно, что составляющие синусоидальные величины должны быть разных частот, так как сложение синусоидальных величин одной и той же частоты приводит к синусоидальной величине той же частоты. Если сложить несколько величин вида ,
, , кратные наименьшей из них,
, кратные наименьшей из них,  , и периоды
, и периоды  , то получится новая периодическая функция (с периодом T), отличная от этих величин.
, то получится новая периодическая функция (с периодом T), отличная от этих величин. . Рассмотрим график этой функции
. Рассмотрим график этой функции
 или просто ее гармониками (первой, второй и т. д.). Процесс разложения периодической функции на гармоники носит название гармонического анализа.
или просто ее гармониками (первой, второй и т. д.). Процесс разложения периодической функции на гармоники носит название гармонического анализа. или
или  (1).
(1). называются коэффициентами тригонометрического ряда. Этот ряд можно записать и так:
называются коэффициентами тригонометрического ряда. Этот ряд можно записать и так: 
 (2)
(2)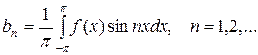 (3)
(3)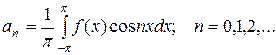 (4)
(4) имеет период 2p и на отрезке
имеет период 2p и на отрезке  непрерывна или имеет конечное число точек разрыва первого рода, отрезок
непрерывна или имеет конечное число точек разрыва первого рода, отрезок  , т.е. среднему арифметическому предельных значений слева и справа.
, т.е. среднему арифметическому предельных значений слева и справа.

 этого ряда:
этого ряда:  .
. и
и  по формулам (3) и (4) соответственно:
по формулам (3) и (4) соответственно:
 Подставляя коэффициенты в формулу (1), получаем
Подставляя коэффициенты в формулу (1), получаем  или
или  .
. и
и  (точки склейки графиков). В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть
(точки склейки графиков). В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть  .
.
 в ряд Фурье.
в ряд Фурье. и
и  по формулам (2-4);
по формулам (2-4); ;
; и на концах отрезка
и на концах отрезка  . В этом случае
. В этом случае 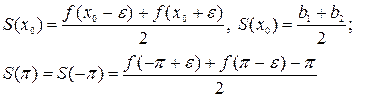
 , где l - любое действительное число, а
, где l - любое действительное число, а  вычислять по формулам:
вычислять по формулам:  ,
,  .
.


