
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрические ряды ФурьеСодержание книги Поиск на нашем сайте
а) Ряд Фурье по ТС (1.4) Теорема 1. (Дирихле). Если
где
сходится к f (x), если x – точка непрерывности f (x) и к
Функция В ряд Фурье можно разложить и непериодическую кусочно-гладкую функцию, заданную лишь в интервале При вычислении коэффициентов Фурье в формулах (3.2) интервал интегрирования б) Неполные ряды Фурье. Если
Ряд Фурье примет вид: Если и ряд Фурье принимает вид в) Функцию г) Комплексная форма тригонометрического ряда Фурье для
Связь между
Пример. Разложить в ряд Фурье периодическую (с периодом Ñ Начертим график заданной функции:
Рис.1.
Запишем ряд Фурье:
(сумма ряда записана в соответствии с теоремой 1: в точках непрерывности Пример. Разложить в ряд Фурье по косинусам
Ñ Продолжим  четным образом на [-2,0], а затем построим периодическое продолжение функции, заданной на [-2,2] на всю ось Ox: четным образом на [-2,0], а затем построим периодическое продолжение функции, заданной на [-2,2] на всю ось Ox:
Рис.2. Получим непрерывную на Ряд Фурье имеет вид:
Ряд Фурье: Пример. Представить рядом Фурье в комплексной форме периодическую функцию
Ñ Построим график данной функции. Рис. 3. Функция является кусочно- гладкой на
Ряд Фурье: Задачи для самостоятельного решения 1. Разложить в ряд Фурье на 2. Разложить в ряд Фурье периодическую 3. Разложить в ряд Фурье на 4. Разложить в интервале а) 5. Дана функция 6. Разложить в ряд Фурье 7. Разложить в ряд Фурье 8. Разложить в ряд Фурье по косинусам 9. Доказать справедливость равенства 10. Представить рядом Фурье в комплексной форме периодическую функцию 11. Разложить в ряд Фурье 12. Разложить в ряд Фурье 13. Разложить в ряд Фурье ИНТЕГРАЛ ФУРЬЕ. ПРЕОБРАЗОВАНИЯ ФУРЬЕ Теорема 2. Если
где
равен Если
Если
Для представления интегралом Фурье функции, заданной лишь в промежутке Если
Положив
получим
Равенство (4.6) называется косинус – преобразованием Аналогично, если
называется синус - преобразованием
называется синус - преобразованием Комплексная форма интеграла Фурье имеет вид
где
Связь между Функция Функция
Пример. Представить интегралом Фурье функцию

Ñ Построим график данной функции. Рис.4. Данная функция 1) имеет 2 точки разрыва I рода Данная функция является непрерывной в интервалах Пример. Показать, что спектральной характеристикой функции
Ñ Построим график данной функции.
Рис.5. Найдем Спектр Построим график
Рис. 6. # Задачи для самостоятельного решения В задачах № 14 – 17 представить интегралом Фурье следующие функции: 14. 16. 18. Функцию 19. Используя результат задачи 18, представить интегралами Фурье функции 1)
20. Написать интеграл Фурье в комплексной форме для функций 1)
21. Вычислить спектр прямоугольного импульса высотой h и длительностью  и построить график спектра. и построить график спектра.
Рис. 7. 22. Записать преобразование Фурье для следующих функций: 1) Ответы к задачам главы 13 1. 2. 3. 5. а) в) г) 6. 8. 10. 11. 14. 16. 18. 1) 19. 1)
21. 22. 1)
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.170.38 (0.006 с.) |

 (на этом интервале f (x) и
(на этом интервале f (x) и  имеют не более конечного числа точек разрыва, притом лишь первого рода), то тригонометрический ряд Фурье по ТС (1.4) для f (x)
имеют не более конечного числа точек разрыва, притом лишь первого рода), то тригонометрический ряд Фурье по ТС (1.4) для f (x)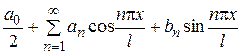 , (3.1)
, (3.1) , n =1,2,3…(3.2)
, n =1,2,3…(3.2) , если x – точка разрыва f (x), где
, если x – точка разрыва f (x), где  и
и  - соответственно левый и правый пределы f (x) в точке x:
- соответственно левый и правый пределы f (x) в точке x:

 - называются коэффициентами Фурье.
- называются коэффициентами Фурье. , совпадающая с
, совпадающая с  , называется периодическим продолжением
, называется периодическим продолжением  длины 2 l.
длины 2 l. . (3.3)
. (3.3) .
. (3.4)
(3.4) .
. , можно разложить в ряд Фурье только по косинусам или по синусам. Для этого достаточно продолжить
, можно разложить в ряд Фурье только по косинусам или по синусам. Для этого достаточно продолжить  и для полученной на
и для полученной на  ,
,  .
. следующая:
следующая: ;
;  ;
;  ;
;  .
. ) функцию
) функцию 

 , периодической с
, периодической с  . Ряд Фурье будет иметь вид:
. Ряд Фурье будет иметь вид:  ;
; 




 .
.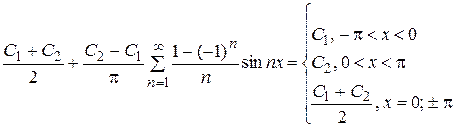
 на отрезке [0,2].
на отрезке [0,2].
 функцию; l = 2.
функцию; l = 2. ;
;




 .
. #
# , определенную для
, определенную для  равенством
равенством  .
.
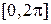 , следовательно, ее можно разложить в ряд Фурье, который будет иметь вид:
, следовательно, ее можно разложить в ряд Фурье, который будет иметь вид:  .
.
 .
. #
# функцию:
функцию:  ;
; равенствами
равенствами 
 .
.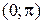 по синусам
по синусам  . Полученное разложение использовать для суммирования числовых рядов
. Полученное разложение использовать для суммирования числовых рядов б)
б) 
 . Разложить ее в ряд Фурье а) в
. Разложить ее в ряд Фурье а) в  .
. на [-1;1].
на [-1;1].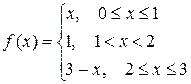 на [0,3].
на [0,3]. .
.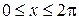 равенством
равенством  ) в комплексной форме:
) в комплексной форме:
 на
на  .
. на
на  .
. ; 2) кусочно-гладкая на каждом конечном отрезке, то ее интеграл Фурье
; 2) кусочно-гладкая на каждом конечном отрезке, то ее интеграл Фурье (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) ,
,  (4.4)
(4.4) ;
;  (4.5)
(4.5)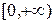 и продолженной четным образом на
и продолженной четным образом на  , используем формулы (4.4), а продолженной нечетным образом – формулы (4.5).
, используем формулы (4.4), а продолженной нечетным образом – формулы (4.5). и
и  , найденные по формулам (4.4), подставить в (4.1), то получим двойной интеграл Фурье для четной функции
, найденные по формулам (4.4), подставить в (4.1), то получим двойной интеграл Фурье для четной функции 
 , (4.6)
, (4.6) (4.7)
(4.7) .
. (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10) (4.11)
(4.11) и
и  :
: 
 называется спектром функции
называется спектром функции  , в этом случае ее обычно обозначают
, в этом случае ее обычно обозначают

 ; 2) абсолютно интегрируема на всей оси Ox:
; 2) абсолютно интегрируема на всей оси Ox:  . 3) данная функция – четная, поэтому на основании (4.4)
. 3) данная функция – четная, поэтому на основании (4.4) 


 .
. ; (-1,1);
; (-1,1);  , кроме того, в точках разрыва среднее арифметическое односторонних пределов функции совпадает со значением ее в этих точках, поэтому можно записать интеграл Фурье
, кроме того, в точках разрыва среднее арифметическое односторонних пределов функции совпадает со значением ее в этих точках, поэтому можно записать интеграл Фурье  . #
. # ,
,  является функция
является функция  . Построить график спектра
. Построить график спектра 



 .
. .
.  .
.
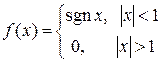 15.
15. 
 17.
17. 
 , представить интегралом Фурье, продолжая ее 1) четным образом, 2) нечетным образом на промежуток
, представить интегралом Фурье, продолжая ее 1) четным образом, 2) нечетным образом на промежуток  и
и  .
. ; 2)
; 2)  .
. , 2)
, 2)  .
.
 ; 2)
; 2)  .
. .
.
 4.
4.  ; а)
; а)  б)
б) 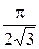
 б)
б) 


 7.
7. 

 ;
; 
 12.
12.  13.
13. 
 15.
15. 
 17.
17. 
 2)
2) 


 2)
2) 
 20. 1)
20. 1)  2)
2) 

 ; 2)
; 2)  .
.


