
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряд Фурье функции, заданной на отрезке длиной 2pСодержание книги
Поиск на нашем сайте 1. Пусть функция f (x) определена и интегрируема на отрезке
где (17) Числа Теорема 7. Если функция f (x) кусочно-гладкая на отрезке [-p,p], т.е. f (x) и ее производная f ¢(x) – непрерывны на отрезке [-p,p] или имеют на нем конечное число точек разрыва первого рода, то ряд Фурье функции f (x) сходится в каждой точке отрезка [-p,p]. При этом сумма S (x), x Î[-p,p], ряда Фурье (16) равна Сумма S (x) ряда Фурье (16) определена для x Î(-¥,+¥) и является 2p – периодической функцией. Пример 1. Разложить функцию f (x)= ex в ряд Фурье в интервале (-p,p). Построить график суммы ряда. Решение. Вычислим коэффициенты Фурье функции по формулам (17), учитывая, что
Поскольку функция ex и ее производная непрерывны на отрезке [-p,p], то по теореме 7 ряд Фурье этой функции сходится к самой функции ex на интервале (-p,p):
Если f (x) – четная функция на отрезке [-p,p], то ее коэффициенты Фурье находятся по формулам , (18) а ряд Фурье имеет вид: , (19) а ряд Фурье имеет вид: Пример 2. Разложить в ряд Фурье функцию Решение. Поскольку функция четная, то
3. Если функция f (x) задана на отрезке [0,p] и удовлетворяет на нем условиям теоремы 7, то ее можно разложить в ряды Фурье различным образом, например, как по косинусам, так и по синусам.
В первом случае продолжают f (x) с интервала (0,p) на интервал
во втором – продолжают f (x) с интервала (0,p) на (-p,0) нечетным образом: f (x)=- f (x), x Î(-p,0) (рис. 1.4), а коэффициенты находят по формулам (19). Пример3. Разложить функцию Решение. Продолжим функцию x 2 с интервала (0,p) на интервал (-p,0) нечетным образом и вычисляем коэффициенты по формулам (19): (Сравните разложение этой же функции x 2 в ряд по косинусам, полученное в примере 2). 4. Если функция f (x) задана на отрезке [ a, a +2p], то ее коэффициенты Фурье вычисляются по формулам:
1.8. Ряд Фурье функции, заданной на отрезке длиной 2 l Пусть функция f (x) определена и интегрируема на отрезке где
Если f (x) – кусочно-гладкая функция на отрезке [- l,l ], то ее ряд Фурье сходится в каждой точке отрезка [- l,l ]. При этом сумма S (x), x Î [- l, l ], ряда Фурье равна
Пример 1. Разложить в ряд Фурье по синусам функцию Решение. Продолжим f (x) на интервале (-2,0) нечетным образом. Тогда
Следовательно, разложение в ряд Фурье имеет вид: 2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ 2.1. Определенный интеграл по фигуре.
Пусть функция f(x,y,z) задана в точках тела W, на поверхности тела Т или кривой Г в декартовой системе координат Oxyz. Разобьем указанные фигуры на n частей D Wi, D Ti, D Гi соответственно и на каждой из частей выберем по одной точке (xi, yi, zi). Меры полученных частей разбиения обозначим через D Vi (обьем части), D Si (площадь части) и D Li (длина части) соответственно. Через Составим теперь интегральные суммы:
Если существуют конечные пределы этих интегральных сумм при l ®0, причем эти пределы не зависят от способа разбиения фигур и от выбора точек на частях разбиения, то они называются определенными интегралами функции f(x,y,z) по названным фигурам:
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 468; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

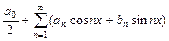 , (16)
, (16)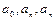 называются коэффициентами Фурье функции f (x).
называются коэффициентами Фурье функции f (x).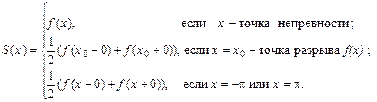 Здесь.
Здесь.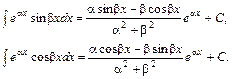
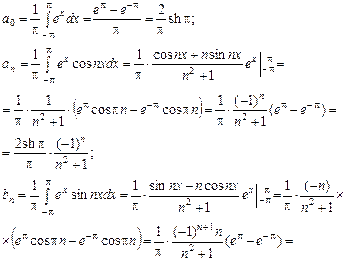


 . Если f (x) – нечетная функция на отрезке [-p,p], то
. Если f (x) – нечетная функция на отрезке [-p,p], то .
. на отрезке [-p,p]. Построить график суммы ряда.
на отрезке [-p,p]. Построить график суммы ряда. находим по формулам (18), применяя интегрирование по частям:
находим по формулам (18), применяя интегрирование по частям: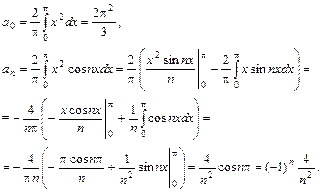
 (в точках x =±p сумма ряда совпадает со значением функции
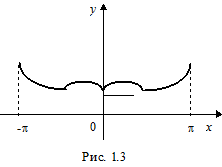
(в точках x =±p сумма ряда совпадает со значением функции  . На рис. 1.2 изображен график суммы данного ряда (пунктиром - график самой функции x 2 вне отрезка [-p,p].
. На рис. 1.2 изображен график суммы данного ряда (пунктиром - график самой функции x 2 вне отрезка [-p,p].

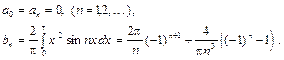
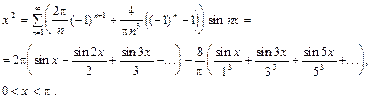

 ,
,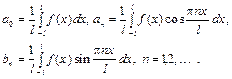

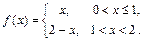
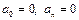 ; при l =2 получаем:
; при l =2 получаем: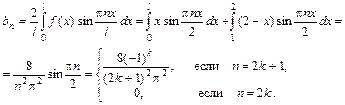
 .
.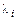 обозначим наибольшее из расстояний между любыми двумя точками, взятыми на i -ой части разбиения,
обозначим наибольшее из расстояний между любыми двумя точками, взятыми на i -ой части разбиения,  . Число
. Число  , показывает, насколько мелко разбиты фигуры, и называется диаметром разбиения.
, показывает, насколько мелко разбиты фигуры, и называется диаметром разбиения.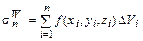 ;
;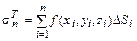 ;
;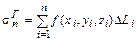 .
. - тройной интеграл;
- тройной интеграл;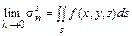 - поверхностный интеграл I рода;
- поверхностный интеграл I рода;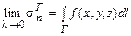 - криволинейный интеграл I рода.
- криволинейный интеграл I рода.


