
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ряды Фурье. Коэффициенты ФурьеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Функциональный ряд вида
или ряд вида
называется тригонометрическим рядом. Постоянные числа Если ряд сходится, то его сумма есть периодическая функция с периодом 2p, так как Пусть периодическая с периодом 2p функция f (x) такова, что она представляется тригонометрическим рядом, сходящимся к данной функции в интервале (-p, p), т.е. является суммой этого ряда
Предположим, что интеграл от функции f (x) равняется сумме интегралов от членов ряда. Это, например, будет выполняться, если предположить, что числовой ряд
сходится. Тогда ряд мажорируем и, следовательно, его можно интегрировать в промежутке (-p, p). Используем это для вычисления коэффициента а 0. Проинтегрируем обе части равенства в пределах от -p до p:
Следовательно,
Неизвестные коэффициенты an и bn можно найти по следующим формулам (вывод этих формул можно найти в любом учебнике по высшей математике)
Коэффициенты, определенные по формулам -, называются коэффициентами Фурье функции f (x), а тригонометрический ряд с такими коэффициентами называется рядом Фурье функции f (x). Выясним, далее, вопрос: какими свойствами должна обладать функция, чтобы построенный для нее ряд Фурье сходился и чтобы сумма этого ряда равнялась значениям данной функции в соответствующих точках?
Определение 10.14.1.Функция f (x) называется кусочно-монотонной на [ a, b ], если этот отрезок можно разбить конечным числом точек х 1, х 2, …, хn -1 на интервалы (а, х 1), (х 1, х 2), …, (хn -1, b), в каждом из которых функция монотонна, т.е. либо невозрастающая, либо неубывающая. Из этого определения следует, что если функция f (x) кусочно-монотонная и ограниченная на [ a, b ], то она может иметь только точки разрыва первого рода. Действительно, если х = С есть точка разрыва функции f (x), то в силу ее монотонности и ограниченности существуют конечные пределы Замечание.В некоторых учебниках функцию f (x), определенную на [ a, b ], называют кусочно-гладкой (кусочно-дифференцируемой), если она и ее производная имеют не более конечного числа точек разрыва, и притом лишь первого рода, т.е. если функция кусочно-монотонная и ограниченная, то она кусочно-гладкая.
Сформулируем теперь следующую теорему.
Теорема 10.14.1(Дирихле). Если периодическая функция с периодом 2p кусочно-монотонная и ограниченная на [-p, p], то ряд Фурье, построенный для этой функции, сходится во всех точках. Сумма полученного ряда S (x) равна значению функции f (x) в точках непрерывности функции. В точках разрыва функции f (x) сумма ряда равна среднему арифметическому пределов функции f (x) слева и справа, т.е., если х = С – точка разрыва первого рода функции f (x), то
Из этой теоремы следует, что класс функций, представимых рядами Фурье, довольно широк. Поэтому ряды Фурье нашли широкое применение в различных разделах математики. Особенно успешно ряды Фурье применяются в математической физике и ее приложениях к конкретным задачам механики и физики. Рассмотрим пример разложения функции в ряд Фурье.
Пример 10.14.1. Периодическая с периодом 2p функция
Очевидно, что функция кусочно-монотонная и ограниченная, т.е. удовлетворяет всем условиям теоремы Дирихле. Определим коэффициенты Фурье:
Таким образом, ряд Фурье будет иметь вид:
В точках разрыва сумма ряда
Полагая в полученном равенстве х =0, получаем
Ранее мы доказывали, что такой числовой ряд сходится (его можно считать обобщенным гармоническим рядом, где Так как по предположению f (x) - 2p-периодическая функция, то отрезок интегрирования [-p, p] в формулах - может быть заменен произвольным отрезком [ а, а+ 2p] длиной 2p. Тогда коэффициенты Фурье могут быть вычислены по формулам:
|
||||||||
|
Последнее изменение этой страницы: 2016-12-16; просмотров: 2511; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.58.191 (0.008 с.) |


 ,
, ,
,  называются коэффициентами тригонометрического ряда.
называются коэффициентами тригонометрического ряда.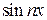 и cos nx являются периодическими функциями с периодом 2p.
и cos nx являются периодическими функциями с периодом 2p. .
.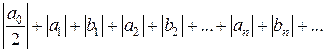
 .
. ,
,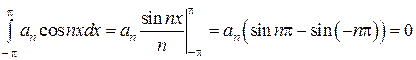 , так как
, так как  для любого n =1, 2, ….
для любого n =1, 2, …. , так как
, так как  .
. , откуда
, откуда .
. ,
, .
. ,
,  .
.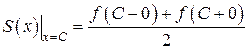 .
.

 ;
;
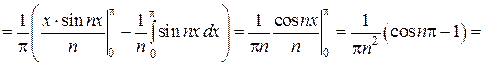
 .
.

 .
.
 .
. .
. , откуда
, откуда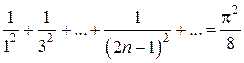 .
. ), а сейчас при помощи ряда Фурье нашли его сумму
), а сейчас при помощи ряда Фурье нашли его сумму  .
. ,
,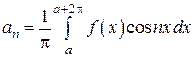 ,
, .
.


