
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поясните понятие обобщенного ряда ФурьеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Обобщенный ряд Фурье. В теории и технике передачи аналоговых сообщений широко используется разложение непрерывных функций на интервале определения Ряд (1), в котором коэффициенты Сn определены по данной формуле называются обобщенным рядом Фурье по данной системе При этом система функций В общем случае ряд (1) для непрерывных сигналов содержит бесконечное число членов. Для практических расчетов такой ряд обычно усекают до N-го члена ряда, и имеет место аппроксимация сигнала
при заданном N по какому-либо определенному критерию. Обычно в качестве критерия приближения используют среднеквадратическую погрешность
Для того, чтобы разложение сигнала в форме (1) было возможным, системы базисных функций (СБФ) должна удовлетворять ряду требований:
Наиболее удобно производить разложение сигналов, если базисная система 22. Запишите основные формулы прямого и обратного преобразования Фурье для непрерывного и дискретного сигналов
Обобщенный ряд Фурье. В теории и технике передачи аналоговых сообщений широко используется разложение непрерывных функций на интервале определения
При этом система функций В общем случае ряд (1) для непрерывных сигналов содержит бесконечное число членов. Для практических расчетов такой ряд обычно усекают до N-го члена ряда, и имеет место аппроксимация сигнала При представлении сигналов в форме (1) необходимо решить вопрос о способе вычисления спектральных коэффициентов. Он во многом будет зависеть от принятого критерия сходимости (приближения). Для среднеквадратичного критерия коэффициенты Сn выбирают таким образом, чтобы СКП была минимальной. Умножив обе части уравнения (1) на Ряд (1), в котором коэффициенты Сn определены по данной формуле называются обобщенным рядом Фурье по данной системе До сих пор мы говорим о непрерывных сигналах. Рассмотрим представление с помощью спектров дискретных сигналов. Решетчатая функция x(i), по любым полным и ортогональным системам решетчатых базисных функций (в дальнейшем БФ) Условия ортогональности и нормированности дискретных СБФ определяются уравнениями:
а равенство Парсеваля для дискретных сигналов имеет вид а Для дискретных функций, удовлетворяющих условию справедлива следующая формула для определения спектра Формулы (3) и (4) представляют собой дискретные преобразования Фурье. Число СБФ в дискретном ряде совпадает с размерностью раскладываемой решетчатой функции N. В соответствии с этим дискретные ряды Фурье () для сигналов с ограниченным интервалом определения имеют конечный характер и дискретные функции воспроизводятся с их помощью точно. Это принципиально отличает их от непрерывных разложений, где суммирование ведется по бесконечному числу членов и которые воспроизводят не саму функцию, а ее копию, совпадающую с ней при
|
||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 952; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.241.93 (0.01 с.) |

 в ряд
в ряд  (1)
(1) . Совокупность коэффициентов
. Совокупность коэффициентов  называется спектром сигнала x(t) в ортогональной системе
называется спектром сигнала x(t) в ортогональной системе  называется базисной, а представление сигнала в виде (1) – его разложением по системе базисных функций или обобщенным рядом. Если сигнал
называется базисной, а представление сигнала в виде (1) – его разложением по системе базисных функций или обобщенным рядом. Если сигнал 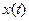 является комплексным, то и коэффициенты
является комплексным, то и коэффициенты  также будут являться комплексными.
также будут являться комплексными. позволяющих технически просто получить набор коэффициентов
позволяющих технически просто получить набор коэффициентов  и минимизирующих погрешность
и минимизирующих погрешность
 .
. удовлетворяющего условию
удовлетворяющего условию  (условие конечности энергии на интервале определения
(условие конечности энергии на интервале определения  является ортогональной на интервале определения сигнала
является ортогональной на интервале определения сигнала 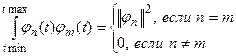
 , проинтегрировав в пределах
, проинтегрировав в пределах  и учтя ортогональность функций
и учтя ортогональность функций  и
и  , получим важное соотношение
, получим важное соотношение  (2)
(2) записывается в виде обобщенного дискретного ряда
записывается в виде обобщенного дискретного ряда  (3)
(3) . При этом моменты отсчетов БФ должны совпадать с моментами отсчетов раскладываемых сигналов.
. При этом моменты отсчетов БФ должны совпадать с моментами отсчетов раскладываемых сигналов.


 - мощность БФ.
- мощность БФ.
 (4)
(4) .
.


