Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тригонометрический ряд ФурьеСодержание книги Поиск на нашем сайте
С помощью так называемого тригонометрического ряда любую (практически) периодическую функцию можно представить в виде ряда, членами которого являются простые гармоники. Определение 4.1. Тригонометрическим рядом называется функциональный ряд вида
где действительные числа Свободный член ряда записан в виде Приведем формулы, которые помогут найти коэффициенты ряда (4.3) Считая (1) Если Если (2) При любом (3) Если
(4) При любых
(5) Если
Если
Замечания.
обладают свойством ортогональности: интеграл от произведения любых двух функций этого семейства на интервале, имеющем длину
Пусть
Так как функция
Интегралы от всех, кроме нулевых членов ряда равны нулю в силу формул (1) и (2). Отсюда
Умножив обе части равенства (4.4) на
В силу формул (1), (3) и (4) из последнего равенства при
Отсюда
Аналогично, умножив равенство (4.4) на
Итак, заранее предполагая, что функция Определение 4.2. Ряд вида:
называется рядом Фурье функции Коэффициентами Фурье функции
Разложение в ряд Фурье
Выясним условия, при которых ряд Фурье функции Будем рассматривать функции Сформулируем теорему (без доказательства), представляющую достаточное условие разложимости функции в ряд Фурье.
Теорема 4.1 (теорема Дирихле). Пусть 1. 2. Тогда соответствующей функции
3. в точках
Таким образом, если функция В силу периодичности функции и суммы ряда Фурье может быть получено указанное разложение во всей области определения функции. Если функция Надо отметить, что условиям теоремы Дирихле удовлетворяют большинство функций, встречающихся в математике и ее приложениях. Существуют функции, не удовлетворяющие условиям теоремы Дирихле, но при этом их можно разложить в ряд Фурье, т.е. теорема Дирихле дает лишь достаточное условие разложимости, но не необходимое.
Пример 4.1. Разложить в ряд Фурье функцию
Решение. Построим график функции
Эта функция удовлетворяет условиям теоремы Дирихле. Значит, ее можно разложить в ряд Фурье. Находим коэффициенты ряда:
Исходной функции
или
В точках разрыва первого рода
В точках
График
,
Разложение в ряд Фурье Четных и нечетных функций
Если разлагаемая на отрезке
Допустим, что разлагаемая в ряд Фурье функция Итак, если функция
где
Допустим, что разлагаемая в ряд Фурье функция Итак, если функция
где Ряды (4.8) и (4.9) называются неполными тригонометрическими рядами, или рядами по косинусам и по синусам соответственно.
Пример 4.2. Разложить в ряд Фурье функцию Решение. Построим график функции
Эта функция удовлетворяет условиям теоремы Дирихле. Значит, ее можно разложить в ряд Дирихле. Функция Находим коэффициент
Таким образом,
или
В точках
График
,
Разложение в ряд Фурье
|
||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1266; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.99.221 (0.007 с.) |

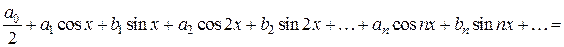
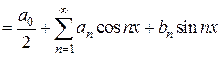 , (4.3)
, (4.3)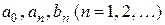 называются коэффициентами ряда.
называются коэффициентами ряда.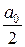 для единообразия получающихся в дальнейшем формул.
для единообразия получающихся в дальнейшем формул.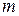 и
и  целыми положительными числами, находим:
целыми положительными числами, находим: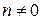 , то
, то 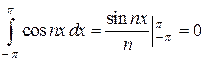 ;
;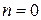 , то
, то 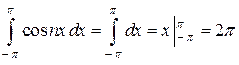 .
.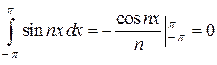 .
.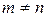 , то
, то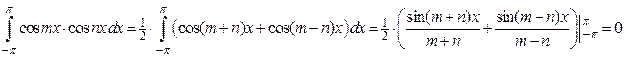 Если
Если 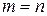 , то
, то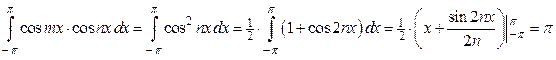 .
.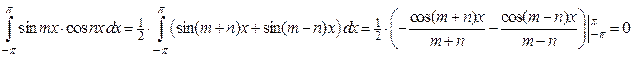
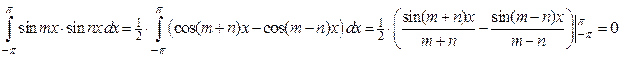
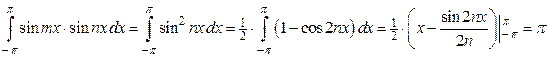 .
.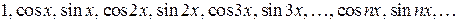
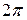 , равен нулю.
, равен нулю.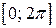 .
. - произвольная периодическая функция с периодом
- произвольная периодическая функция с периодом 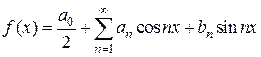 . (4.4)
. (4.4)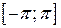 (также удобно взять отрезок
(также удобно взять отрезок 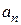 и
и 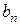 . Для этого проинтегрируем обе части равенства (4.4) в пределах от
. Для этого проинтегрируем обе части равенства (4.4) в пределах от 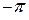 до
до 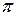 .
.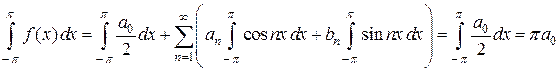 .
.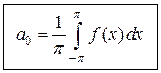 . (4.5)
. (4.5)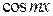 и проинтегрировав полученный ряд в пределах от
и проинтегрировав полученный ряд в пределах от 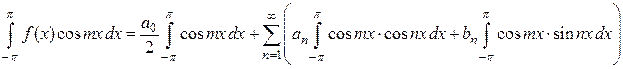
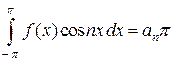 .
.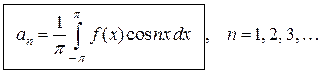 . (4.6)
. (4.6)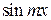 и проинтегрировав почленно на отрезке
и проинтегрировав почленно на отрезке 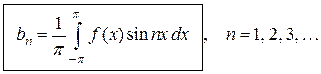 . (4.7)
. (4.7)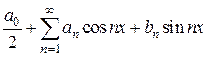
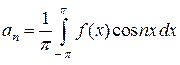 ,
, 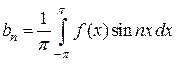 , где
, где 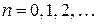 .
.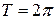 . Такие функции называются
. Такие функции называются  совпадает с самой функцией
совпадает с самой функцией 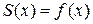 ;
; функции сумма ряда равна среднему арифметическому пределов функции
функции сумма ряда равна среднему арифметическому пределов функции 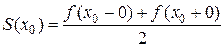 ;
;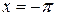 и
и 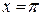 (на концах отрезка) сумма ряда равна
(на концах отрезка) сумма ряда равна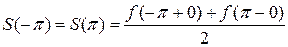 .
.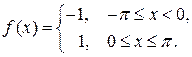
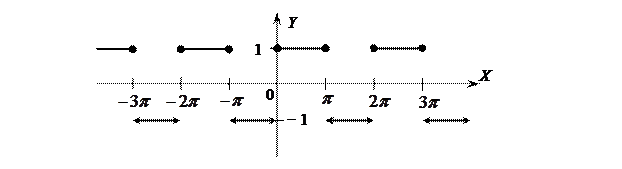
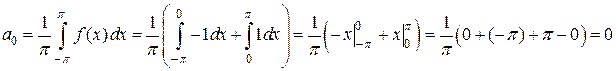 .
.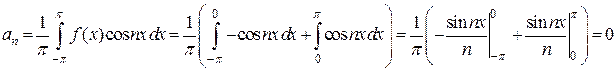 .
.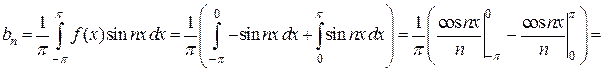
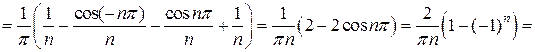
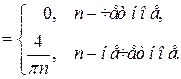
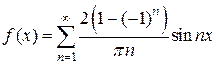 ,
,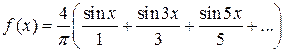 .
.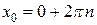 сумма ряда равна:
сумма ряда равна: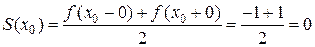 .
.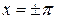 сумма ряда равна:
сумма ряда равна: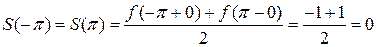 .
.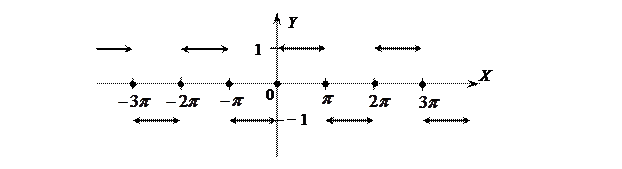
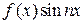 будут нечетными и все коэффициенты
будут нечетными и все коэффициенты 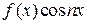 будут четными.
будут четными.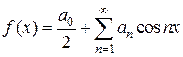 , (4.8)
, (4.8)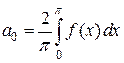 ,
, 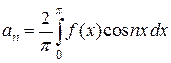 ,
, 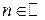 .
.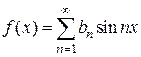 , (4.9)
, (4.9)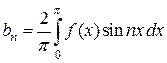 ,
, 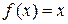 ,
, 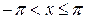 .
.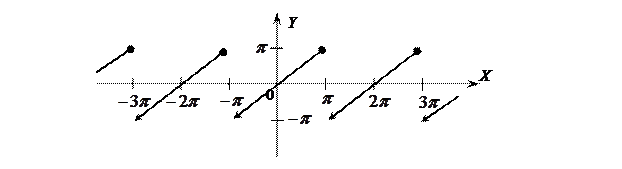
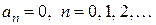 .
.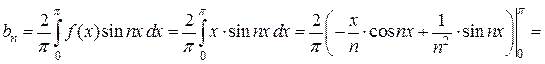
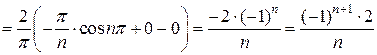 .
.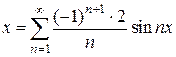 ,
,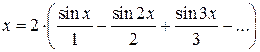 .
.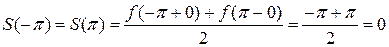 .
.