
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Приближенное решение дифференциальных уравненийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения можно воспользоваться рядом Тейлора. Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.
При решении задачи Коши
используется ряд Тейлора
где Надо отметить, что способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.
Пример 3.12. Найти пять первых членов (отличных от нуля) разложения в степенной ряд решения дифференциального уравнения
Решение. Находим решение дифференциального уравнения (при
Далее находим производные высших порядков и значения производных при
Подставляя найденные значения производных в искомый ряд, получаем:
,
Этот способ приближенного решения наиболее удобен для линейных дифференциальных уравнений с переменными коэффициентами. Пусть, например, требуется решить уравнение
с начальными условиями Предполагая, что коэффициенты
с неопределенными коэффициентами. При помощи начальных условий находим коэффициенты Построенный степенной ряд сходится в том же интервале
Пример 3.13. Найти решение уравнения
используя метод неопределенных коэффициентов. Решение. Разложим коэффициенты уравнения
Решение исходного дифференциального уравнения находим в виде степенного ряда
Тогда
Из начальных условий находим:
Приравнивая коэффициенты при одинаковых степенях
……………………………
Отсюда находим, что
т.е. , 4. РЯДЫ ФУРЬЕ
Периодические функции. Периодические процессы
При изучении разнообразных периодических процессов, т.е. процессов, которые через определенный промежуток времени повторяются (они встречаются в радиотехнике, электротехнике, теории упругости, теории и практике автоматического регулирования и т.д.), целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд. Напомним, что функция
Для построения графика периодической функции периода Отметим основные свойства периодической функции.
Простейшими периодическими функциями являются тригонометрические функции
Простейшим периодическим процессом (движением) является простое гармоническое колебание (движение), описываемое функцией
где
Функция такого вида и ее график называют простой гармоникой. Основным периодом функции (4.1) является Проведем преобразования функции (4.1):
или
где Сложное гармоническое колебание, возникающее в результате наложения конечного (или бесконечного) числа простых гармоник, также описывается функциями вида Возникает вопрос: всякую ли периодическую функцию, описывающую периодический процесс, можно представить в виде суммы простых гармоник вида (4.1) или (4.2)? Если да, то, как найти неизвестные параметры (коэффициенты) каждой из этих гармоник? Ответим сначала на второй вопрос, а потом и на первый.
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 2858; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

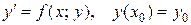 ,
,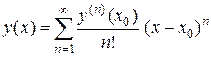 ,
, , а остальные производные
, а остальные производные  находятся путем последовательного дифференцирования уравнения
находятся путем последовательного дифференцирования уравнения  и подстановки начальных данных в выражения для этих производных.
и подстановки начальных данных в выражения для этих производных. , если
, если 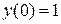 .
. ) в виде
) в виде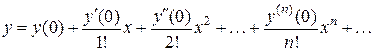 .
. .
. . Тогда
. Тогда 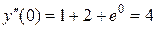 .
. . Тогда
. Тогда  .
.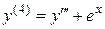 . Тогда
. Тогда  .
. .
.
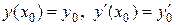 .
. и свободный член
и свободный член  разлагаются в ряды по степеням
разлагаются в ряды по степеням  , сходящиеся в некотором интервале
, сходящиеся в некотором интервале 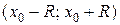 , искомое решение
, искомое решение 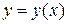 находится в виде степенного ряда
находится в виде степенного ряда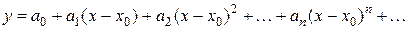
 и
и 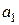 . Для нахождения последующих коэффициентов степенной ряд дифференцируем два раза (каков порядок уравнения) и подставляем выражения для функции
. Для нахождения последующих коэффициентов степенной ряд дифференцируем два раза (каков порядок уравнения) и подставляем выражения для функции 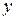 и ее производных в исходное уравнение, заменив в нем
и ее производных в исходное уравнение, заменив в нем  .
. ,
, .
. .
.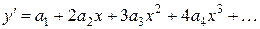 ,
, .
. . Подставляем полученные ряды в дифференциальное уравнение:
. Подставляем полученные ряды в дифференциальное уравнение: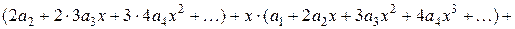
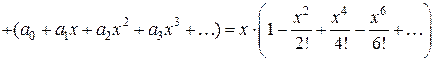 .
.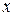 :
: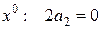 ,
,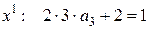 ,
, ,
, ,
,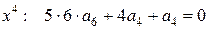 ,
,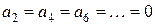 ,
, 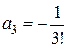 ,
, 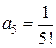 ,
,  , …. Таким образом, получаем решение уравнения в виде
, …. Таким образом, получаем решение уравнения в виде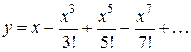 ,
, .
. , определенная на множестве
, определенная на множестве  , называется периодической с периодом
, называется периодической с периодом  , если при каждом
, если при каждом  значение
значение 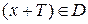 и выполняется равенство
и выполняется равенство 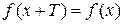 .
. достаточно построить его на любом отрезке длины
достаточно построить его на любом отрезке длины 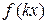 имеет период
имеет период 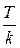 .
.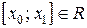 , то
, то 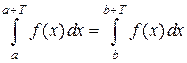 при любых
при любых  и
и 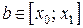 .
.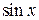 и
и 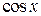 . Период этих функций равен
. Период этих функций равен 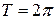 .
.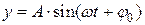 , (4.1)
, (4.1) ,
, 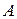 - амплитуда колебания,
- амплитуда колебания,  - частота,
- частота,  - начальная фаза.
- начальная фаза. .
. 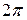 единиц времени.
единиц времени.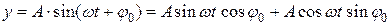 ,
, , (4.2)
, (4.2)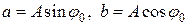 . Отсюда видно, что простое гармоническое колебание описывается периодическими функциями
. Отсюда видно, что простое гармоническое колебание описывается периодическими функциями  и
и  .
.


